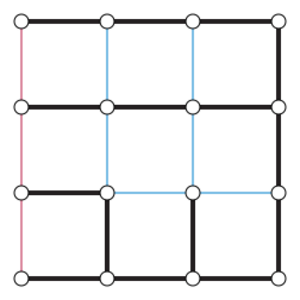
Xuong tree

A Xuong tree. Only one component of the non-tree edges (the red component) has an odd number of edges, the minimum possible for this graph.

In graph theory, a Xuong tree is a spanning tree [math]\displaystyle{ T }[/math] of a given graph [math]\displaystyle{ G }[/math] with the property that, in the remaining graph [math]\displaystyle{ G-T }[/math], the number of connected components with an odd number of edges is as small as possible. They are named after Nguyen Huy Xuong, who used them to characterize the cellular embeddings of a given graph having the largest possible genus.

According to Xuong's results, if [math]\displaystyle{ T }[/math] is a Xuong tree and the numbers of edges in the components of [math]\displaystyle{ G-T }[/math] are [math]\displaystyle{ m_1,m_2,\dots, m_k }[/math], then the maximum genus of an embedding of [math]\displaystyle{ G }[/math] is [math]\displaystyle{ \textstyle\sum_{i=1}^k\lfloor m_i/2\rfloor }[/math]. Any one of these components, having [math]\displaystyle{ m_i }[/math] edges, can be partitioned into [math]\displaystyle{ \lfloor m_i/2\rfloor }[/math] edge-disjoint two-edge paths, with possibly one additional left-over edge. An embedding of maximum genus may be obtained from a planar embedding of the Xuong tree by adding each two-edge path to the embedding in such a way that it increases the genus by one.

A Xuong tree, and a maximum-genus embedding derived from it, may be found in any graph in polynomial time, by a transformation to a more general computational problem on matroids, the matroid parity problem for linear matroids.