Herschel–Bulkley fluid

The Herschel–Bulkley fluid is a generalized model of a non-Newtonian fluid, in which the strain experienced by the fluid is related to the stress in a complicated, non-linear way. Three parameters characterize this relationship: the consistency k, the flow index n, and the yield shear stress [math]\displaystyle{ \tau_0 }[/math]. The consistency is a simple constant of proportionality, while the flow index measures the degree to which the fluid is shear-thinning or shear-thickening. Ordinary paint is one example of a shear-thinning fluid, while oobleck provides one realization of a shear-thickening fluid. Finally, the yield stress quantifies the amount of stress that the fluid may experience before it yields and begins to flow. This non-Newtonian fluid model was introduced by Winslow Herschel and Ronald Bulkley in 1926.

Definition

In one dimension, the constitutive equation of the Herschel-Bulkley model after the yield stress has been reached can be written in the form:

[math]\displaystyle{ \dot{\gamma} = 0, \qquad\qquad \mathrm{if}\ \tau \lt \tau_{0} }[/math]

[math]\displaystyle{ \tau = \tau_{0} + k \dot{\gamma} ^ {n}, \qquad\mathrm{if}\ \tau \geq \tau_{0} }[/math]

where [math]\displaystyle{ \tau }[/math] is the shear stress [Pa], [math]\displaystyle{ \tau_{0} }[/math] the yield stress [Pa], [math]\displaystyle{ k }[/math] the consistency index [Pa[math]\displaystyle{ \cdot }[/math]s[math]\displaystyle{ ^{n} }[/math]], [math]\displaystyle{ \dot{\gamma} }[/math] the shear rate [s[math]\displaystyle{ ^{-1} }[/math]], and [math]\displaystyle{ n }[/math] the flow index [dimensionless]. If [math]\displaystyle{ \tau \lt \tau_{0} }[/math] the Herschel-Bulkley fluid behaves as a rigid (non-deformable) solid, otherwise it behaves as a fluid. For [math]\displaystyle{ n\lt 1 }[/math] the fluid is shear-thinning, whereas for [math]\displaystyle{ n\gt 1 }[/math] the fluid is shear-thickening. If [math]\displaystyle{ n=1 }[/math] and [math]\displaystyle{ \tau_0=0 }[/math], this model reduces to that of a Newtonian fluid.

Reformulated as a tensor, we can instead write:

[math]\displaystyle{ \underline{\underline{\dot{\gamma}}} = 0, \qquad\qquad\qquad\qquad \mathrm{if}\ |\underline{\underline{\tau}}| \lt \tau_{0} }[/math]

[math]\displaystyle{ \underline{\underline{\tau}} =\left(\frac{\tau_{0}}{|\underline{\underline{\dot{\gamma}}}|} + k |\underline{\underline{\dot{\gamma}}}| ^ {n-1}\right)\underline{\underline{\dot{\gamma}}}, \qquad\qquad \mathrm{if}\ |\underline{\underline{\tau}}| \geq \tau_{0} }[/math]

Note that the double underlines indicate a tensor quantity.

Modelling Herschel-Bulkley fluids using regularization

The viscosity associated with the Herschel-Bulkley stress diverges to infinity as the strain rate approaches zero. This divergence makes the model difficult to implement in numerical simulations, so it is common to implement regularized models with an upper limiting viscosity. For instance, the Herschel-Bulkley fluid can be approximated as a generalized Newtonian fluid model with an effective (or apparent) viscosity being given as

[math]\displaystyle{ \mu_{\operatorname{eff}} = \begin{cases} \mu_0, & |\dot{\gamma}| \leq \dot{\gamma}_0 \\ \tau_0 |\dot{\gamma}|^{-1} + k |\dot{\gamma}|^{n-1}, & |\dot{\gamma}| \geq \dot{\gamma}_0 \end{cases} }[/math]

Here, the limiting viscosity [math]\displaystyle{ \mu_0 }[/math] replaces the divergence at low strain rates. Its value is chosen such that [math]\displaystyle{ \mu_0=k \dot{\gamma}_0^{n-1}+\tau_0 \dot{\gamma}_0^{-1} }[/math] to ensure the viscosity is a continuous function of strain rate. A large limiting viscosity means that the fluid will only flow in response to a large applied force. This feature captures the Bingham-type behaviour of the fluid. It is not entirely possible to capture rigid behavior described by the constitutive equation of the Herschel-Bulkley model using a regularised model. This is because a finite effective viscosity will always lead to a small degree of yielding under the influence of external forces (e.g. gravity). The characteristic timescale of the phenomenon being studied is thus an important consideration when choosing a regularisation threshold.

In an incompressible flow, the viscous stress tensor is given as a viscosity, multiplied by the rate-of-strain tensor

[math]\displaystyle{ \tau_{ij} = 2 \mu_{\operatorname{eff}}(|\dot{\gamma}|) E_{ij} = \mu_{\operatorname{eff}}(|\dot{\gamma}|) \left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right), }[/math]

(Note that [math]\displaystyle{ \mu_{\operatorname{eff}}(|\dot{\gamma}|) }[/math] indicates that the effective viscosity is a function of the shear rate.) Furthermore, the magnitude of the shear rate is given by

[math]\displaystyle{ |\dot{\gamma}|=\sqrt{2E_{ij}E^{ij}} }[/math].

The magnitude of the shear rate is an isotropic approximation, and it is coupled with the second invariant of the rate-of-strain tensor

[math]\displaystyle{ II_E = tr(E_{ij} E^{jk}) = E_{ij}E^{ij} }[/math].

Channel flow

A schematic diagram pressure-driven horizontal flow. The flow is uni-directional in the direction of the pressure gradient.

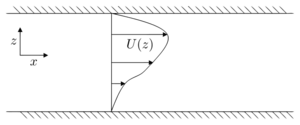
A frequently-encountered situation in experiments is pressure-driven channel flow (see diagram). This situation exhibits an equilibrium in which there is flow only in the horizontal direction (along the pressure-gradient direction), and the pressure gradient and viscous effects are in balance. Then, the Navier-Stokes equations, together with the rheological model, reduce to a single equation:

Velocity profile of the Herschel–Bulkley fluid for various flow indices n. In each case, the non-dimensional pressure is [math]\displaystyle{ \pi_0=-10 }[/math]. The continuous curve is for an ordinary Newtonian fluid (Poiseuille flow), the broken-line curve is for a shear-thickening fluid, while the dotted-line curve is for a shear-thinning fluid.

[math]\displaystyle{ \frac{\partial p}{\partial x}=\frac{\partial}{\partial z}\left(\mu\frac{\partial u}{\partial z}\right)\,\,\, =\begin{cases}\mu_0\frac{\partial^2 u}{\partial{z}^2},&\left|\frac{\partial u}{\partial z}\right|\lt \gamma_0\\ \\\frac{\partial}{\partial z}\left[\left(k\left|\frac{\partial u}{\partial z}\right|^{n-1}+\tau_0\left|\frac{\partial u}{\partial z}\right|^{-1}\right)\frac{\partial u}{\partial z}\right],&\left|\frac{\partial u}{\partial z}\right|\geq\gamma_0\end{cases} }[/math]

To solve this equation it is necessary to non-dimensionalize the quantities involved. The channel depth H is chosen as a length scale, the mean velocity V is taken as a velocity scale, and the pressure scale is taken to be [math]\displaystyle{ P_0=k\left(V/H\right)^n }[/math]. This analysis introduces the non-dimensional pressure gradient

[math]\displaystyle{ \pi_0=\frac{H}{P_0}\frac{\partial p}{\partial x}, }[/math]

which is negative for flow from left to right, and the Bingham number:

[math]\displaystyle{ Bn=\frac{\tau_0}{k}\left(\frac{H}{V}\right)^n. }[/math]

Next, the domain of the solution is broken up into three parts, valid for a negative pressure gradient:

• A region close to the bottom wall where [math]\displaystyle{ \partial u/\partial z\gt \gamma_0 }[/math];
• A region in the fluid core where [math]\displaystyle{ |\partial u/\partial z|\lt \gamma_0 }[/math];
• A region close to the top wall where [math]\displaystyle{ \partial u/\partial z\lt -\gamma_0 }[/math],

Solving this equation gives the velocity profile:

[math]\displaystyle{ u\left(z\right)=\begin{cases} \frac{n}{n+1}\frac{1}{\pi_0}\left[\left(\pi_0\left(z-z_1\right)+\gamma_0^n\right)^{1+\left(1/n\right)}-\left(-\pi_0z_1+\gamma_0^n\right)^{1+\left(1/n\right)}\right],&z\in\left[0,z_1\right]\\ \frac{\pi_0}{2\mu_0}\left(z^2-z\right)+k,&z\in\left[z_1,z_2\right],\\ \frac{n}{n+1}\frac{1}{\pi_0}\left[\left(-\pi_0\left(z-z_2\right)+\gamma_0^n\right)^{1+\left(1/n\right)}-\left(-\pi_0\left(1-z_2\right)+\gamma_0^n\right)^{1+\left(1/n\right)}\right],&z\in\left[z_2,1\right]\\ \end{cases} }[/math]

Here k is a matching constant such that [math]\displaystyle{ u\left(z_1\right) }[/math] is continuous. The profile respects the no-slip conditions at the channel boundaries,

[math]\displaystyle{ u(0)=u(1)=0, }[/math]

Using the same continuity arguments, it is shown that [math]\displaystyle{ z_{1,2}=\tfrac{1}{2}\pm\delta }[/math], where

[math]\displaystyle{ \delta=\frac{\gamma_0\mu_0}{|\pi_0|}\leq \tfrac{1}{2}. }[/math]

Since [math]\displaystyle{ \mu_0=\gamma_0^{n-1}+Bn/\gamma_0 }[/math], for a given [math]\displaystyle{ \left(\gamma_0,Bn\right) }[/math] pair, there is a critical pressure gradient

[math]\displaystyle{ |\pi_{0,\mathrm{c}}|=2\left(\gamma_0+Bn\right). }[/math]

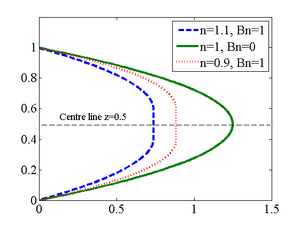
Apply any pressure gradient smaller in magnitude than this critical value, and the fluid will not flow; its Bingham nature is thus apparent. Any pressure gradient greater in magnitude than this critical value will result in flow. The flow associated with a shear-thickening fluid is retarded relative to that associated with a shear-thinning fluid.

Pipe flow

For laminar flow Chilton and Stainsby provide the following equation to calculate the pressure drop. The equation requires an iterative solution to extract the pressure drop, as it is present on both sides of the equation.

[math]\displaystyle{ \frac {\Delta P} {L} = \frac {4 K} {D} \left( \frac {8 V} {D} \right) ^ n \left( \frac {3 n + 1} {4 n} \right) ^ n \frac {1} {1 - X} \left( \frac {1} {1 - a X - b X^2 - cX^3} \right) ^ n }[/math]

[math]\displaystyle{ X = \frac {4 L \tau_ y} {D \Delta P} }[/math]

[math]\displaystyle{ a = \frac {1} {2 n + 1} }[/math]

[math]\displaystyle{ b = \frac {2 n} { \left( n + 1 \right) \left( 2 n + 1 \right) } }[/math]

[math]\displaystyle{ c = \frac {2 n ^ 2} { \left( n + 1 \right) \left( 2 n + 1 \right) } }[/math]

For turbulent flow the authors propose a method that requires knowledge of the wall shear stress, but do not provide a method to calculate the wall shear stress. Their procedure is expanded in Hathoot

[math]\displaystyle{ R = \frac {4 n \rho V D \left( 1 - a X - b X^2 - cX^3 \right)} {\mu_{Wall} \left(3 n + 1 \right) } }[/math]

[math]\displaystyle{ \mu_{Wall} = \tau_{Wall}^{1 - 1/n} \left( \frac {K} {1 - X} \right) ^ {1/n} }[/math]

[math]\displaystyle{ \tau_{Wall} = \frac {D \Delta P} {4 L} }[/math]

All units are SI

[math]\displaystyle{ \Delta P }[/math] Pressure drop, Pa.

[math]\displaystyle{ L }[/math] Pipe length, m

[math]\displaystyle{ D }[/math] Pipe diameter, m

[math]\displaystyle{ V }[/math] Mean fluid velocity, [math]\displaystyle{ m/s }[/math]

Chilton and Stainsby state that defining the Reynolds number as

[math]\displaystyle{ Re = \frac {R} {n ^ 2 \left( 1 - X \right) ^ 4} }[/math]

allows standard Newtonian friction factor correlations to be used.

The pressure drop can then be calculated, given a suitable friction factor correlation. An iterative procedure is required, as the pressure drop is required to initiate the calculations as well as be the outcome of them.

See also

• Viscosity

External links

• Description of Herschel–Bulkley fluid; graphical comparison between rheological models