Schild's ladder

Short description: First-order method for approximating parallel transport of a vector along a curve

Two rungs of Schild's ladder. The segments A₁X₁ and A₂X₂ are an approximation to first order of the parallel transport of A₀X₀ along the curve.

In the theory of general relativity, and differential geometry more generally, Schild's ladder is a first-order method for approximating parallel transport of a vector along a curve using only affinely parametrized geodesics. The method is named for Alfred Schild, who introduced the method during lectures at Princeton University.

Construction

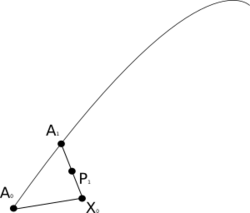
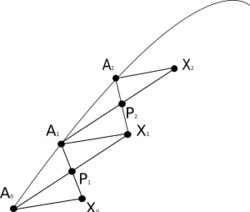
The idea is to identify a tangent vector x at a point [math]\displaystyle{ A_0 }[/math] with a geodesic segment of unit length [math]\displaystyle{ A_0X_0 }[/math], and to construct an approximate parallelogram with approximately parallel sides [math]\displaystyle{ A_0X_0 }[/math] and [math]\displaystyle{ A_1X_1 }[/math] as an approximation of the Levi-Civita parallelogramoid; the new segment [math]\displaystyle{ A_1X_1 }[/math] thus corresponds to an approximately parallel translated tangent vector at [math]\displaystyle{ A_1. }[/math]

A curve in M with a "vector" X0 at A0, identified here as a geodesic segment.

Select A1 on the original curve. The point P1 is the midpoint of the geodesic segment X0A1.

The point X1 is obtained by following the geodesic A0P1 for twice its parameter length.

Formally, consider a curve γ through a point A₀ in a Riemannian manifold M, and let x be a tangent vector at A₀. Then x can be identified with a geodesic segment A₀X₀ via the exponential map. This geodesic σ satisfies

[math]\displaystyle{ \sigma(0)=A_0\, }[/math]

[math]\displaystyle{ \sigma'(0) = x.\, }[/math]

The steps of the Schild's ladder construction are:

• Let X₀ = σ(1), so the geodesic segment [math]\displaystyle{ A_0X_0 }[/math] has unit length.
• Now let A₁ be a point on γ close to A₀, and construct the geodesic X₀A₁.
• Let P₁ be the midpoint of X₀A₁ in the sense that the segments X₀P₁ and P₁A₁ take an equal affine parameter to traverse.
• Construct the geodesic A₀P₁, and extend it to a point X₁ so that the parameter length of A₀X₁ is double that of A₀P₁.
• Finally construct the geodesic A₁X₁. The tangent to this geodesic x₁ is then the parallel transport of X₀ to A₁, at least to first order.

Approximation

This is a discrete approximation of the continuous process of parallel transport. If the ambient space is flat, this is exactly parallel transport, and the steps define parallelograms, which agree with the Levi-Civita parallelogramoid.

In a curved space, the error is given by holonomy around the triangle [math]\displaystyle{ A_1A_0X_0, }[/math] which is equal to the integral of the curvature over the interior of the triangle, by the Ambrose-Singer theorem; this is a form of Green's theorem (integral around a curve related to integral over interior), and in the case of Levi-Civita connections on surfaces, of Gauss–Bonnet theorem.

Notes

1. Schild's ladder requires not only geodesics but also relative distance along geodesics. Relative distance may be provided by affine parametrization of geodesics, from which the required midpoints may be determined.
2. The parallel transport which is constructed by Schild's ladder is necessarily torsion-free.
3. A Riemannian metric is not required to generate the geodesics. But if the geodesics are generated from a Riemannian metric, the parallel transport which is constructed in the limit by Schild's ladder is the same as the Levi-Civita connection because this connection is defined to be torsion-free.

References

• Kheyfets, Arkady; Miller, Warner A.; Newton, Gregory A. (2000), "Schild's ladder parallel transport procedure for an arbitrary connection", International Journal of Theoretical Physics 39 (12): 2891–2898, doi:10.1023/A:1026473418439 .
• Misner, Charles W.; Thorne, Kip S.; Wheeler, John A. (1973), Gravitation, W. H. Freeman, ISBN 0-7167-0344-0