Fokas method
The Fokas method, or unified transform, is an algorithmic procedure for analysing boundary value problems for linear partial differential equations and for an important class of nonlinear PDEs belonging to the so-called integrable systems. It is named after Greek mathematician Athanassios S. Fokas. Traditionally, linear boundary value problems are analysed using either integral transforms and infinite series, or by employing appropriate fundamental solutions.
Integral transforms and infinite series
For example, the Dirichlet problem of the heat equation on the half-line, i.e., the problem
-
[math]\displaystyle{ u_t=u_{xx},\quad 0\lt x\lt \infty, \quad t\gt 0, }[/math]
()
-
[math]\displaystyle{ u(x,0)=u_0(x),\quad 0\lt x\lt \infty;\quad u(0,t)=g_0(t),\quad t\gt 0, }[/math]
()
[math]\displaystyle{ u_0 }[/math] and [math]\displaystyle{ g_0 }[/math] given, can be solved via the sine-transform. The analogous problem on a finite interval can be solved via an infinite series. However, the solutions obtained via integral transforms and infinite series have several disadvantages:
1. The relevant representations are not uniformly convergent at the boundaries. For example, using the sine-transform, equations Eq.1 and Eq.2 imply
-
[math]\displaystyle{ u(x,t)=\frac 2 \pi \int_0^\infty\sin(\lambda x)e^{-\lambda^2 t} \left[ \int_0^\infty \sin(\lambda y) u_0(y) \, dy + \lambda\int_0^te^{\lambda^2\tau} g_0(\tau) \, d\tau \right] \, d\lambda. }[/math]
()
For [math]\displaystyle{ g_0(t)\neq 0 }[/math], this representation cannot be uniformly convergent at [math]\displaystyle{ x=0 }[/math], otherwise one could compute [math]\displaystyle{ u(0,t) }[/math] by inserting the limit [math]\displaystyle{ x\rightarrow 0 }[/math] inside the integral of the rhs of Eq.3 and this would yield zero instead of [math]\displaystyle{ g_0(t) }[/math].
2. The above representations are unsuitable for numerical computations. This fact is a direct consequence of 1.
3. There exist traditional integral transforms and infinite series representations only for a very limited class of boundary value problems.
For example, there does not exist the analogue of the sine-transform for solving the following simple problem:
-
[math]\displaystyle{ u_t+u_{xxx}=0,\quad 0\lt x\lt \infty,\quad t\gt 0, }[/math]
()
supplemented with the initial and boundary conditions Eq.2.
For evolution PDEs, the Fokas method:
- Constructs representations which are always uniformly convergent at the boundaries.
- These representations can be used in a straightforward way, for example using MATLAB, for the numerical evaluation of the solution.
- Constructs representations for evolution PDEs with spatial derivatives of any order.
In addition, the Fokas method constructs representations which are always of the form of the Ehrenpreis fundamental principle.
Fundamental solutions
For example, the solutions of the Laplace, modified Helmholtz and Helmholtz equations in the interior of the two-dimensional domain [math]\displaystyle{ \Omega }[/math], can be expressed as integrals along the boundary of [math]\displaystyle{ \Omega }[/math]. However, these representations involve both the Dirichlet and the Neumann boundary values, thus since only one of these boundary values is known from the given data, the above representations are not effective. In order to obtain an effective representation, one needs to characterize the generalized Dirichlet to Neumann map; for example, for the Dirichlet problem one needs to obtain the Neumann boundary value in terms of the given Dirichlet datum.
For elliptic PDEs, the Fokas method:
- Provides an elegant formulation of the generalised Dirichlet to Neumann map by deriving an algebraic relation, called the global relation, which couples appropriate transforms of all boundary values.
- For simple domains and a variety of boundary conditions the global relation can be solved analytically. Furthermore, for the case that [math]\displaystyle{ \Omega }[/math] is an arbitrary convex polygon, the global relation can be solved numerically in a straightforward way, for example using MATLAB. Also, for the case that [math]\displaystyle{ \Omega }[/math] is a convex polygon, the Fokas method constructs an integral representation in the Fourier complex plane. By using this representation together with the global relation it is possible to compute the solution numerically inside the polygon in a straightforward semi-analytic manner.
The forced heat equation on the half-line
Let [math]\displaystyle{ u(x,t) }[/math] satisfy the forced heat equation
-
[math]\displaystyle{ u_t-u_{xx}=f(x,t),\ 0\lt x\lt \infty, t\gt 0, }[/math]
()
supplemental with the initial and boundary conditions Eq.2, where [math]\displaystyle{ g(t),\ u_0(x),\ f(x,t) }[/math] are given functions with sufficient smoothness, which decay as [math]\displaystyle{ x\rightarrow \infty }[/math].
The unified transform involves the following three simple steps.
1. By employing the Fourier transform pair
- [math]\displaystyle{ \widehat f(\lambda)=\int_0^\infty e^{-i\lambda x}f(x) \, dx,\quad \operatorname{Im}\lambda\leq 0; }[/math]
-
[math]\displaystyle{ f(x)=\frac 1 {2\pi}\int_{-\infty}^\infty e^{i\lambda x} \hat f(\lambda) \, d\lambda,\quad 0\lt x\lt \infty, }[/math]
()
obtain the global relation.
For equation Eq.5, we find
-
[math]\displaystyle{ e^{\lambda^2 t}\hat u(\lambda,t)=Q(\lambda,t)-\tilde{g_1}(\lambda^2,t)-i\lambda \tilde{g_0}(\lambda^2,t),\quad \operatorname{Im}\lambda\leq 0, }[/math]
()
where the functions [math]\displaystyle{ \hat u, \ Q,\ \tilde{g_1} }[/math] and [math]\displaystyle{ \tilde{g_0} }[/math] are the following integral transforms:
- [math]\displaystyle{ \widehat u(\lambda,t)=\int _0^\infty e^{-i\lambda x}u(x,t)\,dx,\ \operatorname{Im}\lambda\leq 0, }[/math]
- [math]\displaystyle{ Q(\lambda,t)=\int_0^\infty e^{-i\lambda x}u_0(x)dx+\int_0^t \, d\tau \int_0^\infty dx \, e^{-i\lambda x+\lambda^2 \tau} f(x,\tau), \quad \operatorname{Im}\lambda \leq 0, }[/math]
-
[math]\displaystyle{ \tilde{g_1}(\lambda^2,t)=\int_0^t e^{\lambda^2 \tau}u_x(0,\tau) \, d\tau, \quad \tilde{g_0}(\lambda^2,t)=\int_0^t e^{\lambda^2 \tau}u(0,\tau) \, d\tau, \quad \lambda\in \mathbb{C}. }[/math]
()
This step is similar with the first step used for the traditional transforms. However, equation Eq.7 involves the t-transforms of both [math]\displaystyle{ u(0,t) }[/math] and [math]\displaystyle{ u_x(0,t) }[/math], whereas in the case of the sine-transform [math]\displaystyle{ u_x(0,t) }[/math] does not appear in the analogous equation (similarly, in the case of the cosine-transform only [math]\displaystyle{ u_x(0,t) }[/math] appears). On the other hand, equation Eq.7 is valid in the lower-half complex [math]\displaystyle{ \lambda }[/math]-plane, wheres the analogous equations for the sine and cosine transforms are valid only for [math]\displaystyle{ \lambda }[/math] real. The Fokas method is based on the fact that equation Eq.7 has a large domain of validity.
2. By using the inverse Fourier transform, the global relation yields an integral representation on the real line. By deforming the real axis to a contour in the upper half [math]\displaystyle{ \lambda }[/math]-complex plane, it is possible to rewrite this expression as an integral along the contour [math]\displaystyle{ \partial D^+ }[/math], where [math]\displaystyle{ \partial D^+ }[/math] is the boundary of the domain [math]\displaystyle{ D^+ }[/math], which is the part of [math]\displaystyle{ D }[/math] in the upper half complex [math]\displaystyle{ \lambda }[/math] plane, with [math]\displaystyle{ D }[/math] defined by
- [math]\displaystyle{ D:\{\lambda\in \mathbb{C},\ \Re\ \omega(\lambda)\lt 0\}, }[/math] where [math]\displaystyle{ \omega(\lambda) }[/math] is defined by the requirement that [math]\displaystyle{ e^{i\lambda x + \omega(\lambda)t} }[/math] solves the given PDE. For equation Eq.5, equations Eq.6 and Eq.7 imply
-
[math]\displaystyle{ u(x,t)=\frac 1 {2\pi} \int_{-\infty}^\infty e^{i\lambda x-\lambda^2 t} Q(\lambda,t) \, d\lambda - \frac 1 {2\pi} \int_{\partial D^+} e^{i\lambda x-\lambda^2t}[\tilde{g_1}(\lambda^2,t) + i\lambda\tilde{g_0}(\lambda^2,t)] \, d\lambda, }[/math]
()
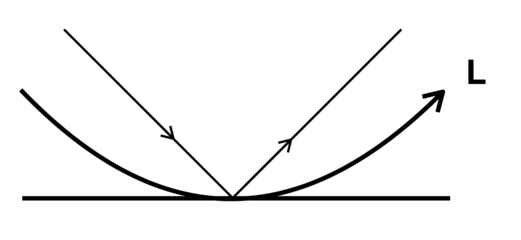
where the contour [math]\displaystyle{ \partial D^+ }[/math] is depicted in figure 1.
In this case, [math]\displaystyle{ \omega(\lambda)=-\lambda^2=-|\lambda|^2e^{2i\theta} }[/math], where [math]\displaystyle{ \theta=\rm{arg}\lambda }[/math]. Thus, [math]\displaystyle{ \Re\ \omega(k)\lt 0 }[/math] implies [math]\displaystyle{ \sin 2\theta\gt 0 }[/math], i.e., [math]\displaystyle{ -\frac{\pi}{4}\lt \theta\lt \frac{\pi}{4} }[/math] and [math]\displaystyle{ \frac{3\pi}{4}\lt \theta\lt \frac{5\pi}{4} }[/math].
The fact that the real axis can be deformed to [math]\displaystyle{ \partial D^+ }[/math] is a consequence of the fact that the relevant integral is an analytic function of [math]\displaystyle{ \lambda }[/math] which decays in [math]\displaystyle{ D^+ }[/math] as [math]\displaystyle{ \lambda\rightarrow\infty }[/math].[1]
3. By using the global relation and by employing the transformations in the complex-[math]\displaystyle{ \lambda }[/math] plane which leave [math]\displaystyle{ \omega(\lambda) }[/math] invariant, it is possible to eliminate from the integral representation of [math]\displaystyle{ u(x,t) }[/math] the transforms of the unknown boundary values. For equation Eq.5, [math]\displaystyle{ \omega(\lambda)=\lambda^2 }[/math], thus the relevant transformation is [math]\displaystyle{ \lambda\rightarrow -\lambda }[/math]. Using this transformation, equation Eq.7 becomes
-
[math]\displaystyle{ e^{\lambda^2 t}\hat u (-\lambda,t)=Q(-\lambda,t)-\tilde{g_1}(\lambda^2,t) + i\lambda \tilde{g_0}(\lambda^2,t),\quad \operatorname{Im} \lambda \geq 0. }[/math]
()
In the case of the Dirichlet problem, solving equation Eq.10 for [math]\displaystyle{ \tilde{g_1} }[/math] and substituting the resulting expression in Eq.9 we find
-
[math]\displaystyle{ u(x,t)=\frac 1 {2\pi}\int_{-\infty}^\infty e^{i\lambda x-\lambda^2 t} Q(\lambda,t) \, d\lambda - \frac 1 {2\pi} \int_{\partial D^+}e^{i\lambda x-\lambda^2t}[2i\lambda\tilde{g_0}(\lambda^2,t)+Q(-\lambda,t)] \, d\lambda. }[/math]
()
If is important to note that the unknown term [math]\displaystyle{ \hat u(-\lambda,t) }[/math] does not contribute to the solution [math]\displaystyle{ u }[/math]. Indeed, the relevant integral involves the term [math]\displaystyle{ e^{i\lambda x}\hat u(-\lambda,t) }[/math], which is analytic and decays as [math]\displaystyle{ \lambda\rightarrow\infty }[/math] in [math]\displaystyle{ D^- }[/math], thus Jordan's lemma implies that [math]\displaystyle{ \hat u(-\lambda,t) }[/math] yields a zero contribution.
Equation Eq.11 can be rewritten in a form which is consistent with the Ehrenpreis fundamental principle: if the boundary condition is specified for [math]\displaystyle{ 0\lt \tau\lt T }[/math], where [math]\displaystyle{ T }[/math] is a given positive constant, then using Cauchy's integral theorem, it follows that Eq.11 is equivalent with the following equation:
-
[math]\displaystyle{ u(x,t)=\frac 1 {2\pi}\int_{-\infty}^\infty e^{i\lambda x-\lambda^2 t} Q(\lambda) \, d\lambda - \frac 1 {2\pi} \int_{\partial D^+} e^{i\lambda x-\lambda^2 t} [Q(-\lambda) + 2i \lambda\tilde{g_0}(\lambda^2)] \, d\lambda, }[/math]
()
where
- [math]\displaystyle{ Q(\lambda)=\widehat u_0(\lambda)+\int_0^\infty dx\int_0^T dt \, e^{-i\lambda x + \lambda^2 t} f(x,t), }[/math]
- [math]\displaystyle{ \tilde{g_0}(\lambda^2)=\int_0^T e^{\lambda^2 t} g_0(t) \, dt. }[/math]
Uniform convergence
The unified transform constructs representations which are always uniformly convergent at the boundaries. For example, evaluating Eq.12 at [math]\displaystyle{ x=0 }[/math], and then letting [math]\displaystyle{ \lambda\rightarrow-\lambda }[/math] in the first term of the second integral in the rhs of Eq.12, it follows that
- [math]\displaystyle{ u(0,t) = -\frac i \pi \int_{\partial D} e^{-\lambda^2 t}\lambda\tilde{g_0}(\lambda^2) \, d\lambda. }[/math]
The change of variables [math]\displaystyle{ \lambda=e^{\frac{i\pi}{4}}\sqrt k }[/math], [math]\displaystyle{ k\gt 0 }[/math], implies that [math]\displaystyle{ u(0,t)=g(t) }[/math].
Numerical evaluation It is straightforward to compute the solution numerically using quadrature after the contour has been deformed to ensure exponential decay of the integrand.[2] For simplicity we concentrate on the case that the relevant transforms can be computed analytically. For example,
- [math]\displaystyle{ f(x,t)=0,\ u_0(x)=e^{-a^2 x}, \ g_0(t)=\cos(bt),\ a, b, \text{real constants}. }[/math]
Then, equation Eq.11 becomes
-
[math]\displaystyle{ 2\pi u(x,t)=\int_{-\infty}^\infty \frac{e^{i\lambda x-\lambda^2 t}}{i\lambda + a^2} \, d\lambda - \int_{\partial D^{+}} e^{i\lambda x-\lambda^2 t} \left[ \frac 1 {-i\lambda +a^2} +\frac{i\lambda }{\lambda +ib}\bigl ( e^{(\lambda^2+ib)t}-1 \bigr) +\frac{i\lambda }{\lambda -ib}\bigl( e^{(\lambda^2-ib)t}-1 \bigr) \right] \, d\lambda . }[/math]
()
For [math]\displaystyle{ \lambda }[/math] on [math]\displaystyle{ \partial D^+ }[/math], the term [math]\displaystyle{ e^{i\lambda x} }[/math] decays exponentially as [math]\displaystyle{ |\lambda|\rightarrow\infty }[/math]. Also by deforming [math]\displaystyle{ \partial D^+ }[/math] to [math]\displaystyle{ L }[/math] where [math]\displaystyle{ L }[/math] is a contour between the real axis and [math]\displaystyle{ \partial D^+ }[/math], it follows that for [math]\displaystyle{ \lambda }[/math] on [math]\displaystyle{ L }[/math] the term [math]\displaystyle{ e^{-\lambda^2 t} }[/math] also decays exponentially as [math]\displaystyle{ |\lambda|\rightarrow\infty }[/math]. Thus, equation Eq.13 becomes
[math]\displaystyle{ 2\pi u(x,t)=\int_L \left\{e^{i\lambda x-\lambda^2 t}\left[ \frac 1 {i\lambda + a^2} + \frac 1 {i\lambda -a^{2}} \right] + i\lambda e^{i\lambda x}\left[ \frac{e^{ibt} - e^{-\lambda^2 t}}{\lambda +ib}+\frac{e^{-ibt}-e^{-\lambda^2 t}}{\lambda -ib} \right] \right\} \, d\lambda, }[/math]
and the rhs of the above equation can be computed using MATLAB.
For the details of effective numerical quadrature using the unified transform, we refer the reader to,[2] which solves the advection-dispersion equation on the half-line. There it was found that the solution lends itself to quadrature (Gauss-Laguerre quadrature for exponential decay of integrand or Gauss–Hermite quadrature for squared exponential decay of integrand) with exponential convergence.
An Evolution Equation with Spatial Derivatives of Arbitrary order.
Suppose that [math]\displaystyle{ e^{i\lambda x+\omega (\lambda)t} }[/math] is a solution of the given PDE. Then, [math]\displaystyle{ \partial D^+ }[/math] is the boundary of the domain [math]\displaystyle{ D^+ }[/math] defined earlier.
If the given PDE contain spatial derivatives of order [math]\displaystyle{ n }[/math], then for [math]\displaystyle{ n }[/math] even, the global relation involves [math]\displaystyle{ \frac{n}{2} }[/math] unknowns, whereas for [math]\displaystyle{ n }[/math] odd it involves [math]\displaystyle{ (n+1)/2 }[/math] or [math]\displaystyle{ (n-1)/2 }[/math] unknowns (depending on the coefficient of the highest derivative). However, using an appropriate number of transformations in the complex [math]\displaystyle{ \lambda }[/math]-plane which leave [math]\displaystyle{ \omega(\lambda) }[/math] invariant, it is possible to obtain the needed number of equations, so that the transforms of the unknown boundary values can be obtained in terms of [math]\displaystyle{ \hat u }[/math] and of the given boundary data in terms of the solution of a system of algebraic equations.
A Numerical Collocation Method
The Fokas method gives rise to a novel spectral collocation method occurring in Fourier space. Recent work has extended the method and demonstrated a number of its advantages; it avoids the computation of singular integrals encountered in more traditional boundary based approaches, it is fast and easy to code up, it can be used for separable PDEs where no Green's function is known analytically and it can be made to converge exponentially with the correct choice of basis functions.
Basic method in a convex bounded polygon
Suppose that [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] both satisfy Laplace's equation in the interior of a convex bounded polygon [math]\displaystyle{ \Omega }[/math]. It follows that
- [math]\displaystyle{ 0=v(u_{xx}+u_{yy})-u(v_{xx}+v_{yy})=\frac{\partial}{\partial x}\big(vu_x-uv_x\big)+\frac{\partial}{\partial y}\big(vu_y-uv_y\big). }[/math]
Then Green's theorem implies the relation
-
[math]\displaystyle{ \int_{\partial\Omega}\left[\left(vu_{x}-uv_{x}\right)dy-\left(vu_{y}-uv_{y}\right)dx\right]=0. }[/math]
()
In order to express the integrand of the above equation in terms of just the Dirichlet and Neumann boundary values, we parameterize [math]\displaystyle{ u(x,y) }[/math] and [math]\displaystyle{ v(x,y) }[/math] in terms of the arc length, [math]\displaystyle{ s }[/math], of [math]\displaystyle{ \partial\Omega }[/math]. This leads to
-
[math]\displaystyle{ u_{x}dy-u_{y}dx=\frac{\partial u}{\partial w}ds, }[/math]
()
where [math]\displaystyle{ \frac{\partial u}{\partial w} }[/math] denotes the normal derivative.
In order to further simplify the global relation, we introduce the complex variable [math]\displaystyle{ z=x+iy }[/math], and its conjugate [math]\displaystyle{ \bar{z}=x-i y }[/math]. We then choose the test function [math]\displaystyle{ v=e^{-i\lambda z} }[/math], leading to the global relation for Laplace's equation:
-
[math]\displaystyle{ \int_{\partial \Omega}e^{-i\lambda z}\left[\frac{\partial u}{\partial w}+\lambda u\frac{dz}{ds}\right]ds=0,\qquad \lambda\in\mathbb{C}. }[/math]
()
A similar argument can also be used in the presence of a forcing term (giving a non-zero right-hand side). An identical argument works for the Helmholtz equation
- [math]\displaystyle{ u_{xx}+u_{yy}+4\beta^2u=0 }[/math]
and the modified Helmholtz equation
- [math]\displaystyle{ u_{xx}+u_{yy}-4\beta^2u=0. }[/math]
Choosing respective test functions [math]\displaystyle{ v=e^{-i\beta(\lambda z+\frac{\bar{z}}{\lambda})} }[/math] and [math]\displaystyle{ v=e^{-i\beta(\lambda z-\frac{\bar{z}}{\lambda})} }[/math] lead to respective global relations
- [math]\displaystyle{ \int_{\partial \Omega}e^{-i\beta(\lambda z+\frac{\bar{z}}{\lambda})}\left[\frac{\partial u}{\partial w}+\beta\left(\lambda \frac{dz}{ds}-\frac{1}{\lambda}\frac{d\bar{z}}{ds}\right)u\right]ds=0, \qquad \lambda\in\mathbb{C}\backslash\{0\}, }[/math]
and
- [math]\displaystyle{ \int_{\partial \Omega}e^{-i\beta(\lambda z-\frac{\bar{z}}{\lambda})}\left[\frac{\partial u}{\partial w}+\beta\left(\lambda \frac{dz}{ds}+\frac{1}{\lambda}\frac{d\bar{z}}{ds}\right)u\right]ds=0, \qquad \lambda\in\mathbb{C}\backslash\{0\}. }[/math]
These three cases deal with more general second order elliptic constant coefficient PDEs through a suitable linear change of variables.
The Dirichlet to Neumann map for a convex polygon Suppose that [math]\displaystyle{ \Omega }[/math] is the interior of a bounded convex polygon specified by the corners [math]\displaystyle{ z_1,z_2,\dots\ z_n }[/math]. In this case, the global relation Eq.16 takes the form
-
[math]\displaystyle{ \sum_{j=1}^n u_j(\lambda)=0,\ \lambda\in \mathbb{C}, }[/math]
()
where
-
[math]\displaystyle{ u_j(\lambda)=\frac 1 2 \int_{z_j}^{z_j+1} e^{-i\lambda z}(u_x-iu_y) \, dz, }[/math]
()
or
-
[math]\displaystyle{ u_j(\lambda)=\int_{z_j}^{z_j+1}e^{-i\lambda z} \left( \frac{\partial u}{\partial w}+\lambda u\frac{dz}{ds} \right) \, ds. }[/math]
()
The side [math]\displaystyle{ S_j }[/math], which is the side between [math]\displaystyle{ z_j }[/math] and [math]\displaystyle{ z_{j+1} }[/math], can be parametrized by
- [math]\displaystyle{ z(t)=m_j+th_j,\ m_j=\frac{z_j+z_{j+1}}{2},\ h_j=\frac{z_{j+1}-z_j}{2},\ t\in [-1,1]. }[/math]
Hence,
- [math]\displaystyle{ ds=|h_j|\,dt,\ dz=h_j \, dt. }[/math]
The functions [math]\displaystyle{ u }[/math] and [math]\displaystyle{ \frac{\partial u}{\partial w} }[/math] can be approximated in terms of Legendre polynomials:
-
[math]\displaystyle{ u^j(t)\approx\sum_{\ell=0}^{N-1}a_\ell^j P_\ell(t),\quad \frac{\partial u^j(t)}{\partial w} \approx\sum_{\ell=0}^{N-1} b_\ell^j P_\ell(t), }[/math]
()
where for the cases of the Dirichlet, Neumann or Robin boundary value problems either [math]\displaystyle{ a_\ell^j }[/math], [math]\displaystyle{ b_\ell^j }[/math]or a linear combination of [math]\displaystyle{ a_\ell^j }[/math]and [math]\displaystyle{ b_\ell^j }[/math] is given.
Equation Eq.19 now becomes an approximate global relation, where
-
[math]\displaystyle{ u_j(\lambda)=\sum_{\ell=0}^{N-1} e^{-im_j\lambda}(b_\ell^j|h_j|+\lambda a_\ell^j h_j) \widehat P_\ell(\lambda h_j),\ \lambda\in \mathbb{C}, }[/math]
()
with [math]\displaystyle{ \hat P_\ell(\lambda) }[/math] denoting the Fourier transform of [math]\displaystyle{ P_\ell(t) }[/math], i.e.,
-
[math]\displaystyle{ \widehat P_\ell(\lambda)=\int_{-1}^1 e^{-i\lambda t}P_\ell(t) \, dt,\quad \lambda\in \mathbb{C}. }[/math]
()
[math]\displaystyle{ \hat P_\ell(\lambda) }[/math] can be computed numerically via [math]\displaystyle{ \hat P_\ell(\lambda)=\frac{\sqrt{-2i\pi\lambda}}{-i\lambda}I_{\ell+\frac{1}{2}}(-i \lambda), }[/math] where [math]\displaystyle{ I_\ell }[/math] denotes the modified Bessel function of the first kind.
The global relation involves [math]\displaystyle{ N }[/math] unknown constants (for the Dirichlet problem, these constants are [math]\displaystyle{ b_\ell^j }[/math]). By evaluating the global relation at a sufficiently large number of different values of [math]\displaystyle{ \lambda }[/math], the unknown constants can be obtained via the solution of a system of algebraic equations.
It is convenient to choose the above values of [math]\displaystyle{ \lambda }[/math] on the [math]\displaystyle{ n }[/math] rays [math]\displaystyle{ -\bar h_j\rho,\ \rho\gt 0,\ j=1,\dots, n. }[/math] For this choice, as [math]\displaystyle{ |\lambda|\rightarrow\infty }[/math], the relevant system is diagonally dominant, thus its condition number is very small.[3]
Dealing with non-convexity
Whilst the global relation is valid for non-convex domains [math]\displaystyle{ \Omega }[/math], the above collocation method becomes numerically unstable.[4] A heuristic explanation for this ill-conditioning in the case of the Laplace equation is as follows. The `test functions' [math]\displaystyle{ e^{-i\lambda z} }[/math] grow/decay exponentially in certain directions of [math]\displaystyle{ \lambda }[/math]. When using a sufficiently large selection of complex [math]\displaystyle{ \lambda }[/math]-values, located in all directions from the origin, each side of a convex polygon will for many of these [math]\displaystyle{ \lambda }[/math]-values encounter larger test functions than do the remaining sides. This is exactly the same argument that motivates the `ray' choice of collocation points given by [math]\displaystyle{ -\overline{h}_j\rho }[/math], which yield a diagonally dominant system. In contrast, for a non-convex polygon, boundary regions in indented regions will always be dominated by effects from other boundary parts, no matter the [math]\displaystyle{ \lambda }[/math]-value. This can easily be overcome by splitting up the domain into numerous convex regions (introducing fictitious boundaries) and matching the solution and normal derivative across these internal boundaries. Such splitting also allows the extension of the method to exterior/unbounded domains [math]\displaystyle{ \Omega }[/math] (see below).
Evaluating in the domain interior
Let [math]\displaystyle{ G=G(z,\zeta) }[/math] be the associated fundamental solution of the PDE satisfied by [math]\displaystyle{ u }[/math]. In the case of straight edges, Green's representation theorem leads to
-
[math]\displaystyle{ \begin{align} u(x,y)&=\sum_{j=1}^n\int_{-1}^1\Big [G(z,\zeta(t))\frac{\partial u}{\partial w}|h_j|+iu\Big (\frac{\partial G}{\partial \zeta(t)}(z,\zeta(t))h_j-\frac{\partial G}{\partial \bar \zeta(t)}(z,\zeta(t))\bar h_j\Big )\Big ]dt\\ &\approx\sum_{j=1}^n\sum_{l=0}^{N-1}\int_{-1}^1\Big [G(z,\zeta(t))b_l^jP_l(t)|h_j|+ia_l^j\Big (\frac{\partial G}{\partial \zeta(t)}(z,\zeta(t))h_j-\frac{\partial G}{\partial \bar \zeta(t)}(z,\zeta(t))\bar h_j\Big )P_l(t)\Big ]dt. \end{align} }[/math]
()
Due to the orthogonality of the Legendre polynomials, for a given [math]\displaystyle{ z=x+iy }[/math], the integrals in the above representation are Legendre expansion coefficients of certain analytic functions (written in terms of [math]\displaystyle{ G }[/math]). Hence the integrals can be computed rapidly (all at once) by expanding the functions in a Chebyshev basis (using the FFT) and then converting to a Legendre basis.[5] This can also be used to approximate the `smooth' part of the solution after adding global singular functions to take care of corner singularities.
Extension to curved boundaries and separable PDEs
The method can be extended to variable coefficient PDEs and curved boundaries in the following manner (see [6]). Suppose that [math]\displaystyle{ \alpha(x,y)\in\mathbb{C}^{2\times 2} }[/math] is a matrix valued function, [math]\displaystyle{ \beta(x,y)\in\mathbb{C}^{2} }[/math] a vector valued function and [math]\displaystyle{ \gamma }[/math] a function (all sufficiently smooth) defined over [math]\displaystyle{ \Omega }[/math]. Consider the formal PDE in divergence form:
-
[math]\displaystyle{ \nabla\cdot(\alpha \nabla u)+\nabla\cdot(\beta u)+\gamma u = 0. }[/math]
()
Assume that the domain [math]\displaystyle{ \Omega }[/math] is a bounded connected Lipschitz domain whose boundary consists of a finite number of vertices connected by [math]\displaystyle{ C^1 }[/math] arcs. Denote the corners of [math]\displaystyle{ \Omega }[/math] in anticlockwise order as [math]\displaystyle{ \{z_j\}_{1}^n }[/math] with the side [math]\displaystyle{ \Gamma_j }[/math], joining [math]\displaystyle{ z_j }[/math] to [math]\displaystyle{ z_{j+1} }[/math]. [math]\displaystyle{ \Gamma_j }[/math] can be parametrised by
- [math]\displaystyle{ [-1,1]\ni t\rightarrow (x_j(t),y_j(t))\in\mathbb{R}^2, }[/math]
where we assume that the parametrisation is [math]\displaystyle{ C^1 }[/math].
The adjoint of equation Eq.24 is given by
-
[math]\displaystyle{ \nabla\cdot(\alpha^T \nabla v)-\beta\cdot\nabla v+\gamma v = 0. }[/math]
()
The expression [math]\displaystyle{ v\times }[/math]Eq.24[math]\displaystyle{ -u\times }[/math]Eq.25 can be written in the form
-
[math]\displaystyle{ \nabla\cdot[v(\alpha \nabla u)-u(\alpha^T \nabla v)+\beta uv]=0. }[/math]
()
Integrating across the domain and applying the divergence theorem we recover the global relation ([math]\displaystyle{ n }[/math] denotes the outward normal):
-
[math]\displaystyle{ \int_{\partial\Omega}u\big[(n\cdot \beta)v-n\cdot(\alpha^T\nabla v)\big]+v\big[n\cdot(\alpha\nabla u)\big]ds=0. }[/math]
()
Define [math]\displaystyle{ l_j(t)=\sqrt{\dot{x}_j(t)^2+\dot{y}_j(t)^2} }[/math] along the curve [math]\displaystyle{ \Gamma_j }[/math] and assume that [math]\displaystyle{ l_j(t)\gt 0 }[/math]. Suppose that we have a one-parameter family of solutions of the adjoint equation, [math]\displaystyle{ v(x,y;\lambda)=v_{\lambda} }[/math], for some [math]\displaystyle{ \lambda\in\mathcal{C} }[/math], where [math]\displaystyle{ \mathcal{C} }[/math] denotes the collocation set. Denoting the solution [math]\displaystyle{ u }[/math] alongside [math]\displaystyle{ \Gamma_j }[/math] by [math]\displaystyle{ u^j }[/math], the unit outward normal by [math]\displaystyle{ n_j }[/math] and analogously the oblique derivative by [math]\displaystyle{ n_j\cdot(\alpha\nabla u^j) }[/math], we define the following important transform:
-
[math]\displaystyle{ \hat{\mu}_j(\lambda):=\int_{-1}^1 \big\{u^j\big[(n_j\cdot \beta)v_{\lambda}-n_j\cdot(\alpha^T\nabla v_{\lambda})\big]+v_{\lambda}\big[n_j\cdot(\alpha\nabla u^j)\big] \big\}l_j(t)dt. }[/math]
()
Using Eq.28 , the global relation Eq.27 becomes
-
[math]\displaystyle{ \sum_{j=1}^n\hat{\mu}_j(\lambda)=0. }[/math]
()
For separable PDEs, a suitable one-parameter family of solutions [math]\displaystyle{ v_{\lambda} }[/math] can be constructed. If we expand each [math]\displaystyle{ u^j }[/math] and its derivative [math]\displaystyle{ n_j\cdot(\alpha\nabla u^j) }[/math] along the boundary [math]\displaystyle{ \Gamma_j }[/math] in Legendre polynomials, then we cover a similar approximate global relation as before. To compute the integrals that form the approximate global relation, we can use the same trick as before - expanding the function integrated against Legendre polynomials in a Chebyshev series and then converting to a Legendre series. A major advantage of the method in this scenario is that it is a boundary-based method which does not need any knowledge of the corresponding Green's function. Hence, it is more applicable than boundary integral methods in the setting of variable coefficients.
Singular functions and an exterior scattering problems
A major advantage of the above collocation method is that the basis choice (Legendre polynomials in the above discussion) can be flexibly chosen to capture local properties of the solution along each boundary. This is useful when the solution has different scalings in different regions of [math]\displaystyle{ \Omega }[/math], but is particularly useful for capturing singular behavior, for example, near sharp corners of [math]\displaystyle{ \Omega }[/math].
We consider the acoustic scattering problem solved in [7] by the method. The solution [math]\displaystyle{ u }[/math] satisfies Helmholtz equation in [math]\displaystyle{ \mathbb{R}^2\backslash \{x\in[-1,1],y=0\} }[/math] with frequency [math]\displaystyle{ k_0=2\beta }[/math], along with the Sommerfeld radiation condition at infinity:
-
[math]\displaystyle{ \lim_{r\rightarrow\infty}r^{1/2}\left(\frac{\partial}{\partial r}-ik_0\right)u(x,y)=0, }[/math]
()
where [math]\displaystyle{ r=\sqrt{x^2+y^2} }[/math]. The boundary condition along the plate is
-
[math]\displaystyle{ \frac{\partial u}{\partial y}(x,0)=-\frac{\partial u_I}{\partial y}(x,0),\quad x\in[-1,1] }[/math]
()
for the incident field
-
[math]\displaystyle{ u_I(x,y)=e^{-ik_0\cos\theta x-ik_0\sin\theta y}. }[/math]
()
By considering the domains [math]\displaystyle{ y\gt 0 }[/math] and [math]\displaystyle{ y\lt 0 }[/math] separately and matching the global relations, the global relation for this problem becomes
-
[math]\displaystyle{ \begin{align} &\int_{\mathbb{R}\backslash [-1,1]}e^{-i\beta x(\lambda+\frac{1}{\lambda})}u_{y}(x,0)dx\\ &+\int_{[-1,1]}e^{-i\beta x(\lambda+\frac{1}{\lambda})}\left[u_{y}(x,0)+\frac{\beta}{2}\left(\lambda-\frac{1}{\lambda}\right)[u](x,0)\right]dx=0, \qquad \lambda\in\Lambda, \end{align} }[/math]
()
with [math]\displaystyle{ \Lambda=(-1,0)\cup(1,\infty)\cup\{e^{-i\theta}:0\lt \theta\lt \pi\} }[/math] and where [math]\displaystyle{ [u](x,0)=u(x,0_+)-u(x,0_-) }[/math] denotes the jump in [math]\displaystyle{ u }[/math] across the plate. The complex collocation points are allowed precisely because of the radiation condition. To capture the endpoint singularities, we expand [math]\displaystyle{ [u](x,0) }[/math] for [math]\displaystyle{ x\in[-1,1] }[/math] in terms of weighted Chebyshev polynomials of the second kind:
-
[math]\displaystyle{ C_m(x)=\sqrt{1-x^2}U_{m}(x). }[/math]
()
These have the following Fourier transform:
-
[math]\displaystyle{ \int_{-1}^1 e^{i\lambda t}\sqrt{1-t^2}U_{m}(t)dt=\frac{(m+1)i^m\pi}{\lambda}J_{m+1}(\lambda), }[/math]
()
where [math]\displaystyle{ J_{\alpha}(\cdot) }[/math] denotes the Bessel function of the first kind of order [math]\displaystyle{ \alpha }[/math]. For the derivative [math]\displaystyle{ u_y }[/math] along [math]\displaystyle{ \mathbb{R}\backslash[-1,1] }[/math], a suitable basis choice are Bessel functions of fractional order (to capture the singularity and algebraic decay at infinity).
We introduce the dimensionless frequency [math]\displaystyle{ \tilde k_0=k_0L^{-1} }[/math], where [math]\displaystyle{ L }[/math] is the length of the plate. The figure below shows the convergence of the method for various [math]\displaystyle{ \tilde k_0 }[/math]. Here [math]\displaystyle{ N }[/math] is the number of basis functions [math]\displaystyle{ C_m }[/math] used to approximate the jump [math]\displaystyle{ [u] }[/math] across the plate. The maximum relative absolute error is the maximum error of the computed solution divided by the maximum absolute value of the solution. The figure is for [math]\displaystyle{ \theta=\pi/3 }[/math] and shows the quadratic-exponential convergence of the method, namely the error decreases like [math]\displaystyle{ \mathcal{O}(\rho^{N^2}) }[/math] for some positive [math]\displaystyle{ \rho\lt 1 }[/math]. More complicated geometries (including different angles of touching boundaries and infinite wedges) can also be dealt with in a similar fashion as well as more complicated boundary conditions such as those modeling elasticity.[8][9]
References
- ↑ Deconinck, B.; Trogdon, T.; Vasan, V. (2014-01-01). "The Method of Fokas for Solving Linear Partial Differential Equations". SIAM Review 56 (1): 159–186. doi:10.1137/110821871. ISSN 0036-1445.
- ↑ 2.0 2.1 de Barros, F. P. J.; Colbrook, M. J.; Fokas, A. S. (2019-08-01). "A hybrid analytical-numerical method for solving advection-dispersion problems on a half-line". International Journal of Heat and Mass Transfer 139: 482–491. doi:10.1016/j.ijheatmasstransfer.2019.05.018. ISSN 0017-9310. https://www.repository.cam.ac.uk/handle/1810/295867.
- ↑ Hashemzadeh, P.; Fokas, A. S.; Smitheman, S. A. (2015-03-08). "A numerical technique for linear elliptic partial differential equations in polygonal domains" (in en). Proc. R. Soc. A 471 (2175): 20140747. doi:10.1098/rspa.2014.0747. ISSN 1364-5021. PMID 25792955. Bibcode: 2015RSPSA.47140747H.
- ↑ Colbrook, Matthew J.; Flyer, Natasha; Fornberg, Bengt (1 December 2018). "On the Fokas method for the solution of elliptic problems in both convex and non-convex polygonal domains". Journal of Computational Physics 374: 996–1016. doi:10.1016/j.jcp.2018.08.005. ISSN 0021-9991. Bibcode: 2018JCoPh.374..996C. https://scholar.colorado.edu/appm_facpapers/26.
- ↑ Colbrook, Matthew J.; Fokas, Thanasis S.; Hashemzadeh, Parham (9 April 2019). "A Hybrid Analytical-Numerical Technique for Elliptic PDEs". SIAM Journal on Scientific Computing 41 (2): A1066–A1090. doi:10.1137/18M1217309. Bibcode: 2019SJSC...41A1066C.
- ↑ Colbrook, Matthew J. (27 November 2018). "Extending the unified transform: curvilinear polygons and variable coefficient PDEs" (in en). IMA Journal of Numerical Analysis 40 (2): 976–1004. doi:10.1093/imanum/dry085.
- ↑ Colbrook, Matthew J.; Ayton, Lorna J.; Fokas, Athanassios S. (28 February 2019). "The unified transform for mixed boundary condition problems in unbounded domains". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 475 (2222): 20180605. doi:10.1098/rspa.2018.0605. PMID 30853842. Bibcode: 2019RSPSA.47580605C.
- ↑ Colbrook, Matthew J.; Ayton, Lorna J. (2019). "A spectral collocation method for acoustic scattering by multiple elastic plates". Journal of Sound and Vibration 461: 114904. doi:10.1016/j.jsv.2019.114904. Bibcode: 2019JSV...46114904C. https://www.repository.cam.ac.uk/handle/1810/295869.
- ↑ Ayton, Lorna J.; Colbrook, Matthew; Fokas, Athanassios (2019). "The Unified Transform: A Spectral Collocation Method for Acoustic Scattering". 25th AIAA/CEAS Aeroacoustics Conference. American Institute of Aeronautics and Astronautics. doi:10.2514/6.2019-2528. ISBN 978-1-62410-588-3. https://www.repository.cam.ac.uk/handle/1810/293418.
 |