Dini's surface
From HandWiki

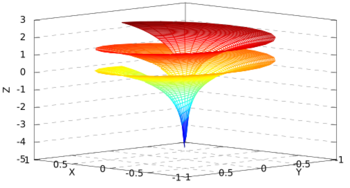
Dini's surface plotted with adjustable parameters by Wolfram Mathematica program
In geometry, Dini's surface is a surface with constant negative curvature that can be created by twisting a pseudosphere.[1] It is named after Ulisse Dini[2] and described by the following parametric equations:[3]
- [math]\displaystyle{ \begin{align} x&=a \cos u \sin v \\ y&=a \sin u \sin v \\ z&=a \left(\cos v +\ln \tan \frac{v}{2} \right) + bu \end{align} }[/math]
Another description is a generalized helicoid constructed from the tractrix.[4]
See also
References
- ↑ "Wolfram Mathworld: Dini's Surface". http://mathworld.wolfram.com/DinisSurface.html. Retrieved 2009-11-12.
- ↑ J J O'Connor and E F Robertson (2000). "Ulisse Dini Biography". School of Mathematics and Statistics, University of St Andrews, Scotland. http://www-gap.dcs.st-and.ac.uk/~history/Biographies/Dini.html. Retrieved 2016-04-12.
- ↑ "Knol: Dini's Surface (geometry)". Archived from the original on 2011-07-23. https://web.archive.org/web/20110723150222/http://knol.google.com/k/suresh-emre/dini-s-surface-geometry/35vsnxisjn2mw/26. Retrieved 2009-11-12.
- ↑ Rogers and Schief (2002). Bäcklund and Darboux transformations: geometry and modern applications in Soliton Theory. Cambridge University Press. pp. 35–36. https://archive.org/details/backlunddarbouxt00schi.