Quadratic pseudo-Boolean optimization
Quadratic pseudo-Boolean optimisation (QPBO) is a combinatorial optimization method for quadratic pseudo-Boolean functions in the form
- [math]\displaystyle{ f(\mathbf{x}) = w_0 + \sum_{p \in V} w_p(x_p) + \sum_{(p, q) \in E} w_{pq}(x_p, x_q) }[/math]
in the binary variables [math]\displaystyle{ x_p \in \{0, 1\} \; \forall p \in V = \{1, \dots, n\} }[/math], with [math]\displaystyle{ E \subseteq V \times V }[/math]. If [math]\displaystyle{ f }[/math] is submodular then QPBO produces a global optimum equivalently to graph cut optimization, while if [math]\displaystyle{ f }[/math] contains non-submodular terms then the algorithm produces a partial solution with specific optimality properties, in both cases in polynomial time.[1]
QPBO is a useful tool for inference on Markov random fields and conditional random fields, and has applications in computer vision problems such as image segmentation and stereo matching.[2]
Optimization of non-submodular functions
If the coefficients [math]\displaystyle{ w_{pq} }[/math] of the quadratic terms satisfy the submodularity condition
- [math]\displaystyle{ w_{pq}(0, 0) + w_{pq}(1, 1) \le w_{pq}(0, 1) + w_{pq}(1, 0) }[/math]
then the function can be efficiently optimised with graph cut optimization. It is indeed possible to represent it with a non-negative weighted graph, and the global minimum can be found in polynomial time by computing a minimum cut of the graph, which can be computed with algorithms such as Ford–Fulkerson, Edmonds–Karp, and Boykov–Kolmogorov's.
If the function is not submodular, then the problem is NP-hard in the general case and it is not always possible to solve it exactly in polynomial time. It is possible to replace the target function with a similar but submodular approximation, e.g. by removing all non-submodular terms or replacing them with submodular approximations, but such approach is generally sub-optimal and it produces satisfying results only if the number of non-submodular terms is relatively small.[1]
QPBO builds an extended graph, introducing a set of auxiliary variables ideally equivalent to the negation of the variables in the problem. If the nodes in the graph associated to a variable (representing the variable itself and its negation) are separated by the minimum cut of the graph in two different connected components, then the optimal value for such variable is well defined, otherwise it is not possible to infer it. Such method produces results generally superior to submodular approximations of the target function.[1]
Properties
QPBO produces a solution where each variable assumes one of three possible values: true, false, and undefined, noted in the following as 1, 0, and [math]\displaystyle{ \emptyset }[/math] respectively. The solution has the following two properties.
- Partial optimality: if [math]\displaystyle{ f }[/math] is submodular, then QPBO produces a global minimum exactly, equivalent to graph cut, and all variables have a non-undefined value; if submodularity is not satisfied, the result will be a partial solution [math]\displaystyle{ \mathbf{x} }[/math] where a subset [math]\displaystyle{ \hat{V} \subseteq V }[/math] of the variables have a non-undefined value. A partial solution is always part of a global solution, i.e. there exists a global minimum point [math]\displaystyle{ \mathbf{x^*} }[/math] for [math]\displaystyle{ f }[/math] such that [math]\displaystyle{ x_i = x_i^* }[/math] for each [math]\displaystyle{ i \in \hat{V} }[/math].
- Persistence: given a solution [math]\displaystyle{ \mathbf{x} }[/math] generated by QPBO and an arbitrary assignment of values [math]\displaystyle{ \mathbf{y} }[/math] to the variables, if a new solution [math]\displaystyle{ \hat{\mathbf{y}} }[/math] is constructed by replacing [math]\displaystyle{ y_i }[/math] with [math]\displaystyle{ x_i }[/math] for each [math]\displaystyle{ i \in \hat{V} }[/math], then [math]\displaystyle{ f(\hat{\mathbf{y}}) \le f(\mathbf{y}) }[/math].[1]
Algorithm
The algorithm can be divided in three steps: graph construction, max-flow computation, and assignment of values to the variables.
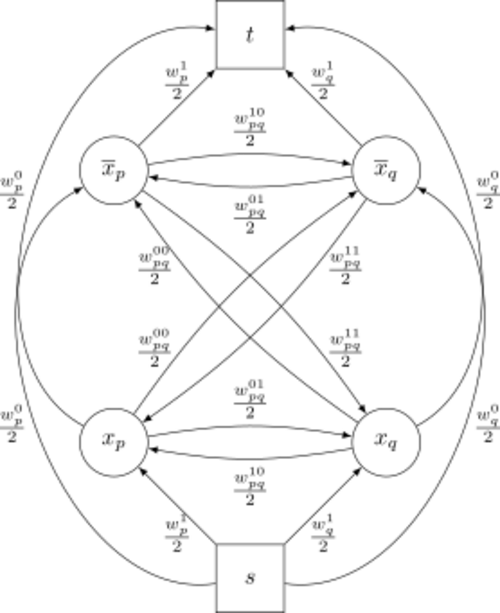
When constructing the graph, the set of vertices [math]\displaystyle{ V }[/math] contains the source and sink nodes [math]\displaystyle{ s }[/math] and [math]\displaystyle{ t }[/math], and a pair of nodes [math]\displaystyle{ p }[/math] and [math]\displaystyle{ p' }[/math] for each variable. After re-parametrising the function to normal form,[note 1] a pair of edges is added to the graph for each term [math]\displaystyle{ w }[/math]:
- for each term [math]\displaystyle{ w_p(0) }[/math] the edges [math]\displaystyle{ p \rightarrow t }[/math] and [math]\displaystyle{ s \rightarrow p' }[/math], with weight [math]\displaystyle{ \frac{1}{2} w_p(0) }[/math];
- for each term [math]\displaystyle{ w_p(1) }[/math] the edges [math]\displaystyle{ s \rightarrow p }[/math] and [math]\displaystyle{ p' \rightarrow t }[/math], with weight [math]\displaystyle{ \frac{1}{2} w_p(1) }[/math];
- for each term [math]\displaystyle{ w_{pq}(0, 1) }[/math] the edges [math]\displaystyle{ p \rightarrow q }[/math] and [math]\displaystyle{ q' \rightarrow p' }[/math], with weight [math]\displaystyle{ \frac{1}{2} w_{pq}(0, 1) }[/math];
- for each term [math]\displaystyle{ w_{pq}(1, 0) }[/math] the edges [math]\displaystyle{ q \rightarrow p }[/math] and [math]\displaystyle{ p' \rightarrow q' }[/math], with weight [math]\displaystyle{ \frac{1}{2} w_{pq}(1, 0) }[/math];
- for each term [math]\displaystyle{ w_{pq}(0, 0) }[/math] the edges [math]\displaystyle{ p \rightarrow q' }[/math] and [math]\displaystyle{ q \rightarrow p' }[/math], with weight [math]\displaystyle{ \frac{1}{2} w_{pq}(0, 0) }[/math];
- for each term [math]\displaystyle{ w_{pq}(1, 1) }[/math] the edges [math]\displaystyle{ q' \rightarrow p }[/math] and [math]\displaystyle{ p' \rightarrow q }[/math], with weight [math]\displaystyle{ \frac{1}{2} w_{pq}(1, 1) }[/math].
The minimum cut of the graph can be computed with a max-flow algorithm. In the general case, the minimum cut is not unique, and each minimum cut correspond to a different partial solution, however it is possible to build a minimum cut such that the number of undefined variables is minimal.
Once the minimum cut is known, each variable receives a value depending upon the position of its corresponding nodes [math]\displaystyle{ p }[/math] and [math]\displaystyle{ p' }[/math]: if [math]\displaystyle{ p }[/math] belongs to the connected component containing the source and [math]\displaystyle{ p' }[/math] belongs to the connected component containing the sink then the variable will have value of 0. Vice versa, if [math]\displaystyle{ p }[/math] belongs to the connected component containing the sink and [math]\displaystyle{ p' }[/math] to the one containing the source, then the variable will have value of 1. If both nodes [math]\displaystyle{ p }[/math] and [math]\displaystyle{ p' }[/math] belong to the same connected component, then the value of the variable will be undefined.[2]
The way undefined variables can be handled is dependent upon the context of the problem. In the general case, given a partition of the graph in two sub-graphs and two solutions, each one optimal for one of the sub-graphs, then it is possible to combine the two solutions into one solution optimal for the whole graph in polynomial time.[3] However, computing an optimal solution for the subset of undefined variables is still a NP-hard problem. In the context of iterative algorithms such as [math]\displaystyle{ \alpha }[/math]-expansion, a reasonable approach is to leave the value of undefined variables unchanged, since the persistence property guarantees that the target function will have non-increasing value.[1] Different exact and approximate strategies to minimise the number of undefined variables exist.[2]
Higher order terms
It is always possible to reduce a higher-order function to a quadratic function which is equivalent with respect to the optimisation, problem known as "higher-order clique reduction" (HOCR), and the result of such reduction can be optimized with QPBO. Generic methods for reduction of arbitrary functions rely on specific substitution rules and in the general case they require the introduction of auxiliary variables.[4] In practice most terms can be reduced without introducing additional variables, resulting in a simpler optimization problem, and the remaining terms can be reduced exactly, with addition of auxiliary variables, or approximately, without addition of any new variable.[5]
Notes
References
- Billionnet, Alain; Jaumard, Brigitte (1989). "A decomposition method for minimizing quadratic pseudo-boolean functions". Operations Research Letters 8 (3): 161–163. doi:10.1016/0167-6377(89)90043-6.
- Fix, Alexander; Gruber, Aritanan; Boros, Endre; Zabih, Ramin (2011). "A graph cut algorithm for higher-order Markov random fields". International Conference on Computer Vision. pp. 1020–1027. https://www.cs.cornell.edu/~afix/Papers/ICCV11.pdf.
- Ishikawa, Hiroshi (2014). "Higher-Order Clique Reduction Without Auxiliary Variables". Conference on Computer Vision and Pattern Recognition. IEEE. pp. 1362–1269. https://www.cv-foundation.org/openaccess/content_cvpr_2014/papers/Ishikawa_Higher-Order_Clique_Reduction_2014_CVPR_paper.pdf.
- Kolmogorov, Vladimir; Rother, Carsten (2007). "Minimizing Nonsubmodular Functions: A Review". IEEE Transactions on Pattern Analysis and Machine Intelligence (IEEE) 29 (7): 1274–1279. doi:10.1109/tpami.2007.1031. PMID 17496384.
- Rother, Carsten; Kolmogorov, Vladimir; Lempitsky, Victor; Szummer, Martin (2007). "Optimizing binary MRFs via extended roof duality". Conference on Computer Vision and Pattern Recognition. pp. 1–8. https://www.microsoft.com/en-us/research/wp-content/uploads/2007/06/cvpr07-QPBOpi-TR.pdf.
Notes
- ↑ The representation of a pseudo-Boolean function with coefficients [math]\displaystyle{ \mathbf{w} = (w_0, w_1, \dots, w_{nn}) }[/math] is not unique, and if two coefficient vectors [math]\displaystyle{ \mathbf{w} }[/math] and [math]\displaystyle{ \mathbf{w}' }[/math] represent the same function then [math]\displaystyle{ \mathbf{w}' }[/math] is said to be a reparametrisation of [math]\displaystyle{ \mathbf{w} }[/math] and vice versa. In some constructions it is useful to ensure that the function has a specific form, called normal form, which is always defined for any function, and it is not unique. A function [math]\displaystyle{ f }[/math] is in normal form if the two following conditions hold (Kolmogorov and Rother (2007)):
- [math]\displaystyle{ \min \{ w_p^0, w_p^1 \} = 0 }[/math] for each [math]\displaystyle{ p \in V }[/math];
- [math]\displaystyle{ \min \{ w_{pq}^{0j}, w_{pq}^{1j} \} = 0 }[/math] for each [math]\displaystyle{ (p, q) \in E }[/math] and for each [math]\displaystyle{ j \in \{0, 1\} }[/math].
- as long as there exist indices [math]\displaystyle{ (p, q) \in E }[/math] and [math]\displaystyle{ j \in \{0, 1\} }[/math] such that the second condition of normality is not satisfied, substitute:
- [math]\displaystyle{ w_{pq}^{0j} }[/math] with [math]\displaystyle{ w_{pq}^{0j} - a }[/math]
- [math]\displaystyle{ w_{pq}^{1j} }[/math] with [math]\displaystyle{ w_{pq}^{1j} - a }[/math]
- [math]\displaystyle{ w_q^j }[/math] with [math]\displaystyle{ w_q^j + a }[/math]
- where [math]\displaystyle{ a = \min \{ w_{pq}^{0j}, w_{pq}^{1j} \} }[/math];
- for [math]\displaystyle{ p = 1, \dots, n }[/math], substitute:
- [math]\displaystyle{ w_0 }[/math] with [math]\displaystyle{ w_0 + a }[/math]
- [math]\displaystyle{ w_p^0 }[/math] with [math]\displaystyle{ w_p^0 - a }[/math]
- [math]\displaystyle{ w_p^1 }[/math] with [math]\displaystyle{ w_p^1 - a }[/math]
- where [math]\displaystyle{ a = \min \{ w_p^0, w_p^1 \} }[/math].
External links
- Implementation of QPBO (C++), available under the GNU General Public License, by Vladimir Kolmogorov.
- Implementation of HOCR (C++), available under the MIT license, by Hiroshi Ishikawa.
 |