Physics:Impossible object

Short description: Type of optical illusion

For John Frankenheimer's film, see Impossible Object. For the independent rock band, see The Impossible Shapes.

An impossible cube

An impossible object (also known as an impossible figure or an undecidable figure) is a type of optical illusion that consists of a two-dimensional figure which is instantly and naturally understood as representing a projection of a three-dimensional object but cannot exist as a solid object. Impossible objects are of interest to psychologists, mathematicians and artists without falling entirely into any one discipline.

Notable examples

Notable impossible objects include:

• Borromean rings — although conventionally drawn as three linked circles in three-dimensional space, any realization must be non-circular
• Impossible cube — invented by M.C. Escher for Belvedere, a lithograph in which a boy seated at the foot of the building holds an impossible cube.
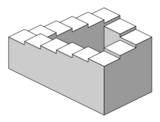
• Penrose stairs – created by Oscar Reutersvärd and later independently devised and popularised by Lionel Penrose and his mathematician son Roger Penrose. A variation on the Penrose triangle, it is a two-dimensional depiction of a staircase in which the stairs make four 90-degree turns as they ascend or descend yet form a continuous loop, so that a person could climb them forever and never get any higher.
• Penrose triangle (Tribar) – first created by the Swedish artist Oscar Reutersvärd in 1934. Roger Penrose independently devised and popularised it in the 1950s, describing it as "impossibility in its purest form".
• Impossible trident (or devil's tuning fork) – The Blivet, has three cylindrical prongs at one end which then mysteriously transform into two rectangular prongs at the other end.
• L'egsistential Quandary – Created by Roger Shepard in 1990, is a drawing of an elephant whose four feet are drawn at the bottom of the white space between legs, instead of on the legs themselves.

Examples of impossible objects

• 

  Borromean rings

• 

  Oscar Reutersvärd's optical illusion (1934)

• 

  Penrose stairs

• 

  Penrose triangle

• 

  Impossible trident

• 

  Impossible waterfall

• 

  A variant of L'egsistential Quandary

Explanations

Impossible objects can be unsettling because of our natural desire to interpret 2D drawings as three-dimensional objects. This is why a drawing of a Necker cube would most likely be seen as a cube, rather than "two squares connected with diagonal lines, a square surrounded by irregular planar figures, or any other planar figure". Looking at different parts of an impossible object makes one reassess the 3D nature of the object, which confuses the mind.

In most cases the impossibility becomes apparent after viewing the figure for a few seconds. However, the initial impression of a 3D object remains even after it has been contradicted. There are also more subtle examples of impossible objects where the impossibility does not become apparent spontaneously and it is necessary to consciously examine the geometry of the implied object to determine that it is impossible.

Roger Penrose wrote about describing and defining impossible objects mathematically using the algebraic topology concept of cohomology.

History

An early example of an impossible object comes from Apolinère Enameled, a 1916 advertisement painted by Marcel Duchamp. It depicts a girl painting a bed-frame with white enamelled paint, and deliberately includes conflicting perspective lines, to produce an impossible object. To emphasise the deliberate impossibility of the shape, a piece of the frame is missing.

A 3D-printed version of the Reutersvärd Triangle illusion, its appearance created by a forced perspective.

Swedish artist Oscar Reutersvärd was one of the first to deliberately design many impossible objects. He has been called "the father of impossible figures". In 1934, he drew the Penrose triangle, some years before the Penroses. In Reutersvärd's version, the sides of the triangle are broken up into cubes.

In 1956, British psychiatrist Lionel Penrose and his son, mathematician Roger Penrose, submitted a short article to the British Journal of Psychology titled "Impossible Objects: A Special Type of Visual Illusion". This was illustrated with the Penrose triangle and Penrose stairs. The article referred to Escher, whose work had sparked their interest in the subject, but not Reutersvärd, of whom they were unaware. The article was published in 1958.

From the 1930s onwards, Dutch artist M.C. Escher produced many drawings featuring paradoxes of perspective gradually working towards impossible objects. In 1957, he produced his first drawing containing a true impossible object: Cube with Magic Ribbons. He produced many further drawings featuring impossible objects, sometimes with the entire drawing being an impossible object. Waterfall and Belvedere are good examples of impossible constructions. His work did much to draw the attention of the public to impossible objects.

Some contemporary artists are also experimenting with impossible figures, for example, Jos de Mey, Shigeo Fukuda, Sandro del Prete, István Orosz (Utisz), Guido Moretti, Tamás F. Farkas, Mathieu Hamaekers, and Kokichi Sugihara.

Constructed impossible objects

Although possible to represent in two dimensions, it is not geometrically possible for such an object to exist in the physical world. However some models of impossible objects have been constructed, such that when they are viewed from a very specific point, the illusion is maintained. Rotating the object or changing the viewpoint breaks the illusion, and therefore many of these models rely on forced perspective or having parts of the model appearing to be further or closer than they actually are.

The notion of an "interactive impossible object" is an impossible object that can be viewed from any angle without breaking the illusion.

As the viewing angle changes of this sculpture in East Perth, Australia, a Penrose triangle appears to form.

See also

• Four-dimensional space – Geometric space with four dimensions
• Mathematics and art – Relationship between mathematics and art
• Möbius strip – Non-orientable surface with one edge
• Physics:Multistable perception – Perceptual phenomenon
• Necker cube – Form of perceptual phenomena
• Non-Euclidean geometry – Two geometries based on axioms closely related to those specifying Euclidean geometry
• Philosophy:Paradox – Statement that apparently contradicts itself
• Physics:Pareidolia – Perception of meaningful patterns or images in random or vague stimuli
• Puzzle – Problem or enigma that tests
• Strange loop – Cyclic structure that goes through several levels in a hierarchical system
• Tesseract – Four-dimensional analogue of the cube
• Tritone paradox – An auditory illusion perceived by some people to be rising in pich and by others to be falling

Further reading

• Bower, Gordon H. (editor), (1990). Psychology of Learning & Motivation. Academic Press. Volume 26. p. 107. ISBN:0080863779
• Mathematical Circus, Martin Gardner 1979 ISBN:0-14-022355-X (Chapter 1 – Optical Illusions)
• Optical Illusions, Bruno Ernst 2006 ISBN:3-8228-5410-7

External links

• Impossible World
• The M.C. Escher Project
• Art of Reutersvard
• "Escher for Real" (3D objects)
• Inconsistent Images
• Echochrome, a video game that incorporates impossible objects into its gameplay