Graphical game theory
In game theory, the common ways to describe a game are the normal form and the extensive form. The graphical form is an alternate compact representation of a game using the interaction among participants. Consider a game with [math]\displaystyle{ n }[/math] players with [math]\displaystyle{ m }[/math] strategies each. We will represent the players as nodes in a graph in which each player has a utility function that depends only on him and his neighbors. As the utility function depends on fewer other players, the graphical representation would be smaller.
Formal definition
A graphical game is represented by a graph [math]\displaystyle{ G }[/math], in which each player is represented by a node, and there is an edge between two nodes [math]\displaystyle{ i }[/math] and [math]\displaystyle{ j }[/math] iff their utility functions are dependent on the strategy which the other player will choose. Each node [math]\displaystyle{ i }[/math] in [math]\displaystyle{ G }[/math] has a function [math]\displaystyle{ u_{i}:\{1\ldots m\}^{d_{i}+1}\rightarrow\mathbb{R} }[/math], where [math]\displaystyle{ d_i }[/math] is the degree of vertex [math]\displaystyle{ i }[/math]. [math]\displaystyle{ u_{i} }[/math] specifies the utility of player [math]\displaystyle{ i }[/math] as a function of his strategy as well as those of his neighbors.
The size of the game's representation
For a general [math]\displaystyle{ n }[/math] players game, in which each player has [math]\displaystyle{ m }[/math] possible strategies, the size of a normal form representation would be [math]\displaystyle{ O(m^{n}) }[/math]. The size of the graphical representation for this game is [math]\displaystyle{ O(m^{d}) }[/math] where [math]\displaystyle{ d }[/math] is the maximal node degree in the graph. If [math]\displaystyle{ d\ll n }[/math], then the graphical game representation is much smaller.
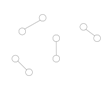
An example
In case where each player's utility function depends only on one other player:
The maximal degree of the graph is 1, and the game can be described as [math]\displaystyle{ n }[/math] functions (tables) of size [math]\displaystyle{ m^{2} }[/math]. So, the total size of the input will be [math]\displaystyle{ nm^{2} }[/math].
Nash equilibrium
Finding Nash equilibrium in a game takes exponential time in the size of the representation. If the graphical representation of the game is a tree, we can find the equilibrium in polynomial time. In the general case, where the maximal degree of a node is 3 or more, the problem is NP-complete.
Further reading
- Michael Kearns (2007) "Graphical Games". In Vazirani, Vijay V.; Nisan, Noam; Roughgarden, Tim; Tardos, Éva (2007). Algorithmic Game Theory. Cambridge, UK: Cambridge University Press. ISBN 0-521-87282-0. http://www.cs.cmu.edu/~sandholm/cs15-892F13/algorithmic-game-theory.pdf.
- Michael Kearns, Michael L. Littman and Satinder Singh (2001) "Graphical Models for Game Theory".
 |