Engineering:Superluminescent diode
A superluminescent diode (SLED or SLD) is an edge-emitting semiconductor light source based on superluminescence. It combines the high power and brightness of laser diodes with the low coherence of conventional light-emitting diodes. Its emission optical bandwidth, also described as full-width at half maximum, can range from 5 up to 750 nm.[1]
History
The superluminescent diode was reported for the first time by Kurbatov et al. (1971)[2][3] and Lee, Burrus, and Miller (1973).[4][3] By 1986 Dr. Gerard A. Alphonse at RCA Laboratories (now SRI International), invented a novel design enabling high power superluminescent diodes.[5] This light source was developed as a key component in the next generations of fibre optic gyroscopes, low coherence tomography for medical imaging, and external cavity tunable lasers with applications to fiber-optic communications. In 1989 the technology was transferred to GE-RCA in Canada , which became a division of EG&G. Superluminescent light emitting diodes are also called sometimes superluminescent diodes, superluminescence diodes or superluminescent LEDs.
Principles of operation
A superluminescent light emitting diode is, similar to a laser diode, based on an electrically driven p-n junction that, when biased in forward direction, becomes optically active and generates amplified spontaneous emission over a wide range of wavelengths. The peak wavelength and the intensity of the SLED depend on the active material composition and on the injection current level. SLEDs are designed to have high single pass amplification for the spontaneous emission generated along the waveguide but, unlike laser diodes, insufficient feedback to achieve lasing action. This is obtained very successfully through the joint action of a tilted waveguide and anti-reflection coated (ARC) facets.
When an electrical forward voltage is applied, an injection current across the active region of the SLED is generated. Like most semiconductor devices, a SLED consists of a positive (p-doped) section and a negative (n-doped) section. Electric current will flow from the p-section to the n-section and across the active region that is sandwiched in between the p- and n-section. During this process, light is generated through spontaneous and random recombination of positive (holes) and negative (electrons) electrical carriers and then amplified when travelling along the waveguide of a SLED.
The pn-junction of the semiconductor material of a SLED is designed in such a way that electrons and holes feature a multitude of possible states (energy bands) with different energies. Therefore, the recombination of electron and holes generates light with a broad range of optical frequencies, i.e. broadband light.
The output power performance of an ideal SLED can be described with a simple model, not taking spectral effects into account and considering both a uniform distribution of carrier densities and zero reflections from the facets.
[math]\displaystyle{ P_{out} = \frac{h}{c} \cdot \nu \cdot \Pi \cdot R_{sp}\frac{\exp[(g-\alpha)L]-1}{g-\alpha} }[/math]
Where h is the Planck constant, ν the optical frequency, Π the size of the optical mode, Rsp the spontaneous emission rate into the guided mode, g the modal gain, α the non-resonant optical losses, L the length of the active channel and c the velocity of light.
So the output power depends linearly on the spontaneous emission rate and exponentially on the optical gain. Obviously a high modal gain is required to obtain high optical output power.
Main characteristics
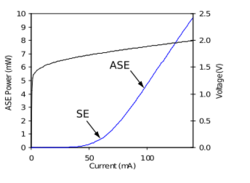
Dependence of power on current
The total optical power emitted by an SLED depends on the drive current. Unlike laser diodes, the output intensity does not exhibit a sharp threshold but it gradually increases with current. A soft knee in the power vs. current curve defines a transition between a regime dominated by spontaneous emission (typical for surface emitting LEDs) and one that is dominated by amplified spontaneous emission (i.e. superluminescence). Even if the output power is based on spontaneous emission it has to be noted that the amplification mechanism affects the polarization state of the emitted radiation in a way which is related to the SLED structure and on the operating conditions.
The maximum value of the current that allows a safe operation of the device depends on the model and ranges between 70 mA (for low power SLED) and 500 mA for the most powerful devices.
Centre wavelength and optical bandwidth
The optical power emitted by SLEDs is distributed over a wide spectral range. Two useful parameters that are related to the power density distribution at different wavelengths are the optical bandwidth (BW) and the peak wavelength, [math]\displaystyle{ \lambda }[/math]peak. The first is defined as the full width at half maximum (FWHM) of the power density vs. wavelength curve at the nominal operating conditions while the latter corresponds to the wavelength having the highest intensity. The centre wavelength, [math]\displaystyle{ \lambda }[/math]centre is defined as the central point between the two FWHM points of the spectral curve; it can be different from the peak wavelength since it is related to the spectrum asymmetry.
Typical values for SLED modules are for the BW between 5 nm and 100 nm with central wavelengths covering the range between 400 nm and 1700 nm. A trade off between maximum output power and bandwidth exists, however, the latter being larger for devices with lower output power.
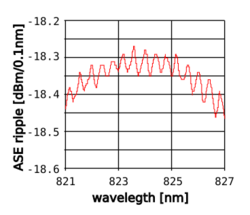
Spectral ripple
The spectral ripple is the measure of the variation of the spectral power-density that can be observed for small change of the wavelength. It can be detected using high-resolution optical spectrum analyzers and can be ascribed to the residual reflectivity of the chip facets and of the coupling fibre. Spectral ripple is more evident in high-power devices and mainly around the peak wavelength where the device gain is higher. It is always present to some extent but undesirable since it has strong effects on the coherence properties of SLED (see section coherence length).
Some SLEDs from certain manufacturers exhibit an extremely low value of the ripple even at the highest power levels. An excessive level of optical back-reflection can cause unexpected irregularities of the spectral distribution of SLEDs that have not to be confused with the ripple. During operation it is therefore important to carefully limit the feedback from any additional equipment.
Polarization
As described above, superluminescent light emitting diodes are based on the generation and on the amplification of spontaneous emission in a semiconductor waveguide. The structure and the material composition used for the SLED chip affect the gain that the radiation experience during the propagation and lead to different amplification factors for different orientations of the electric field (polarization dependent gain). SLEDs operating in the wavelength range of 1300 and 1400 nm are mostly based on a bulk material and a chip structure both characterized by a low polarization dependence of the gain. On the contrary, devices operating in the 1550 and 1620 nm range make mostly use of a quantum well (QW) active region that has a strong polarization-dependent gain. The optical field emitted by the SLED chips, being a combination of unpolarized spontaneous emission and amplified radiation, has therefore a certain degree of polarization (DOP).
A useful quantity that describes the polarization characteristics of the SLED emission is the polarization extinction ratio (PER). This is the ratio between the maximum and the minimum intensities measured after a rotating linear polarizer.
The polarization extinction ratio of bulk chips is around 8–9 dB while it can be as high as 15–20 dB for QW chips. When SLED chips are coupled to pigtail fibres the pigtail bending and coiling will in general modify the polarization state at the fibre output. Modules provided with polarization maintaining (PM) fibre pigtails exhibit high values (>15 dB) of the polarization extinction ratio that are independent on the fibre bending. The polarization extinction ratio of the emission depends also on the drive current, having its highest value at the maximum driving current. On the contrary, the polarization state at the output of standard SM fibre pigtail is arbitrary but can be simply modified with a polarization controller and extinction ratios of about 10 dB can be easily achieved.
Relative intensity noise (RIN)
The optical power emitted by semiconductor active devices is always affected by fluctuations (intensity noise) that are induced by the spontaneous emission. When the emitted power is detected with a wide-bandwidth square-law detector the intensity noise will be converted into current fluctuations and the measured photocurrent will include a constant term, I0, proportional to the mean optical intensity and a time dependent term, In, related to the intensity fluctuations.
The spectral distribution of the noise term in the photocurrent can be measured by means of an electrical spectrum analyzer over a radio frequency (RF) range that is limited by the electrical bandwidth of the detector used. The resultant noise spectrum is directly related to the optical intensity noise and in general depends on the RF frequency, [math]\displaystyle{ \omega }[/math].
From this measurement a useful parameter that provides quantitative information on the noise of the optical source can be evaluated: it is the relative intensity noise (RIN), that is the ratio between the power spectral density of the noise current, In, measured over a given bandwidth, and the square value of the average photocurrent, I0
[math]\displaystyle{ RIN (\omega)= \lt I_{n}^{2}(\omega)\gt /\lt I_{0}^{2}\gt }[/math]
The RIN therefore represents the ratio between the noise power and the average power after detection; the measurement unit used is the dB/Hz. Typical values measured for SLEDs in a frequency range extending from DC up to 500 MHz are reported in the table.
| SLED center wavelength | 100 mA | 150 mA | 200 mA | 300 mA | 400 mA | 500 mA |
|---|---|---|---|---|---|---|
| 1550 nm | −121.5 | −123.5 | ||||
| 1550 nm | −124.5 | −127.5 | −128.0 | −129.5 | −130.0 | |
| 1300 nm | −123.5 | −125.0 | −126.5 | −127.0 | −127.5 | |
| 1300 nm | −124.0 | −124.5 | ||||
| 1600 nm | −123.0 | −123.0 |
They depend on the injection current (more correctly on the output power) and on the RF frequency range. The highest measured values never exceed −119 dB/Hz for frequencies higher than 5 GHz, while the lowest value (around 127 dB/Hz) is attained by the most powerful SLEDs in the 1310 nm window and in the frequency range limited to values less than 500 MHz. The frequency dependence of RIN is thought to be related to spatial correlation effects induced by the gain saturation.
It has to be noted that, while the use of narrow band optical filters in front of a detector will usually result in the reduction of the detected noise, the relative intensity noise of SLEDs can exhibit an increase. This behaviour, present mainly in high power SLEDs, is similar to what is observed with multimode Fabry-Perot laser diodes where filtering makes evident the presence of mode partition noise (mostly at low RF frequencies) due to competition among several lasing modes.
Modulation characteristics
Intensity modulation of SLEDs can be easily achieved through direct modulation of the bias current. SLED modules do not include terminating resistors inside because, operating at relatively high currents, excessive cooling would be required to compensate for the heat dissipation of the resistor. In order to achieve the best performance some external network that reduces the impedance mismatch between the driver amplifier, that usually requires 50 Ohm loads, and the low impedance of the chip (a few Ohm) would be preferable. As shown in Fig. , response times of about 1 ns, extinction ratios of 27 dB and 3 dB bandwidths exceeding 200 MHz can be easily achieved.
Similar results can be obtained also for direct modulation of butterfly packaged SLEDs as shown in Fig. . Optically induced modulation allows to exploit the high speed modulation capabilities of the chip when they are not affected by package parasitics; as shown in Fig. , a 3 dB bandwidth exceeding 10 GHz also for packaged SLEDs can be achieved in this case.
Coherence length
SLEDs are optical sources with a rather wide optical bandwidth. In that they differ from both lasers, that have a very narrow spectrum, and white light sources, that exhibit a much larger spectral width. This characteristic mainly reflects itself in a low temporal coherence of the source (which is the limited capability of the emitted light wave to maintain the phase over time). SLEDs may however exhibit a high degree of spatial coherence, meaning that they can be efficiently coupled into single-mode optical fibers. Some applications take advantage of the low temporal coherence of SLEDs sources to achieve high spatial resolution in imaging techniques. The coherence length, Lc, is a quantity frequently used to characterize the temporal coherence of the light source. It is related to the path difference between the two arms of an optical interferometer over which the light wave is still capable to generate an interference pattern. For sources having a Gaussian spectral distribution, the value of Lc is inversely proportional to the spectral width, BW, so that the full width at half maximum (FWHM) of the power spectral density can be related to Lc through the equation
[math]\displaystyle{ L_{c} = \lambda^{2}/BW }[/math],
where [math]\displaystyle{ \lambda }[/math] is the central wavelength of the emitted radiation. As an example, an SLED operating around 1300 nm and with an optical bandwidth of 100 nm is expected to have a coherence length of about 17 μm. From a practical point of view a definition independent on the spectral distribution (non-Gaussian spectrum) of the source is more suitable. If an optical interferometer is used for the coherence length evaluation (see Fig. 11 a and b) a useful quantity is the FWHM value of the visibility, that is the relative amplitude [(Ipeak - Ivalley) / (Ipeak + Ivalley)] of the intensity variations evaluated as a function of the interferometer imbalance.
SLEDs exhibit a large spectral width even at the highest power levels so that corresponding FWHM values of the visibility less than 20 μm are easily achieved.
The presence of an excessive spectral ripple (see section spectral ripple) in the power spectral density results in the presence of side lobes ) in the visibility curve that can limit both the spatial resolution and the sensitivity of SLED based measurement systems. SLEDs of certain manufacturers have very low side lobes and allow measurements with high dynamic ranges.
Technical challenges
On the one hand SLEDs are semiconductor devices that are optimized to generate a large amount of amplified spontaneous emission (ASE). In order to do that, they incorporate high-power gain sections in which seeding spontaneous emission is amplified with high gain factors of 30 dB or more.
On the other hand, SLEDs lack optical feedback, so that no laser action can occur. Optical feedback resulting from back-reflections of light from optical components such as e.g. connectors into the cavity is suppressed by means of tilting the facets relative to the waveguide, and can be suppressed further with anti-reflection coatings. The formation of resonator modes and thus pronounced structures in the optical spectrum and/or to spectral narrowing are avoided.
It is therefore natural that even small amounts of back-reflections are amplified inside the SLED chip in a similar manner, producing optical power levels of several tens of milliwatts at the back facet, which may destroy the SLED device. SLEDs should be carefully protected against external optical feedback. Even small levels of feedback can reduce the overall emission bandwidth and the output power, or sometimes even lead to parasitic lasing, causing narrow spikes in the emission spectrum. Some devices may even be damaged by optical feedback. Note that the Fresnel reflection from a perpendicularly cleaved fiber end is already well above the level of feedback which can be tolerated. If back reflections cannot be avoided, an optical isolator must be installed directly behind the SLED module. The isolator provides a low insertion loss from the SLED to the fiber and a high insertion loss in the back direction. However, SLEDs from certain component manufacturers are on the market featuring intrinsically safe designs with high robustness against optical back reflections.
To a similar extent as laser diodes, superluminescent light emitting diodes are sensitive to electrostatic discharges and current spikes e.g. from ill-designed driver electronics. When selecting the current source to operate the SLED, special attention should be paid to low-noise specifications. Again certain suppliers are offering driver electronics especially designed to handle on the one hand the high-power, low-noise requirements and on the other hand protect the light sources against discharge and spikes. When treated carefully and operated well within the specifications, SLEDs can easily last for tens of thousands of hours of operation.
Availability
By means of the above-mentioned optimized optical cavity design the SLEDs exhibit high output power, large bandwidth and low residual spectral ripple, making them an ideal light source for a number of applications. Based on the application's requirements and specifications, SLED devices are available in various packages or form factors covering a broad range of wavelengths and power levels. The packages include cooled 14-pin dual-in-line (DIL) and butterfly (BTF) modules or low-cost uncooled TOSA and TO-56 devices. The SLED modules includes indium phosphide (InP) based superluminescent light-emitting diodes operating in the high wavelength range (1100 nm to 1700 nm) as well as gallium arsenide (GaAs) based devices operating from 630 to 1100 nm. Usage of gallium nitride (GaN) based designs is breaking ground for SLEDs in the ultraviolet and blue spectral range.
SLEDs are commercially available from a number of suppliers, e.g. Denselight (Singapore), EXALOS (Switzerland), InPhenix (US), Superlum (Ireland), or Thorlabs Quantum Electronics (US). The product portfolio offered varies greatly from supplier to supplier by wavelength, power, and bandwidth. Other examples include Zeiss Plex Elite 9000 SLD at 750 nm, and LD-PD inc SLDs at 1480 nm and 1530 nm.
Applications
SLEDs find application in situations demanding high intensity and spatial coherence but where a need for a broad, smooth optical output spectrum makes laser diodes unsuitable. Some examples include optical coherence tomography, white light interferometry, optical sensing and fibre optic gyroscopes.
References
- ↑ Ooi, B. S.; Cha, D.; Ng, T. K.; Majid, M. A.; Khan, M. Z. M. (2013-10-01). "Simultaneous quantum dash-well emission in a chirped dash-in-well superluminescent diode with spectral bandwidth >700 nm" (in EN). Optics Letters 38 (19): 3720–3723. doi:10.1364/OL.38.003720. ISSN 1539-4794. PMID 24081035.
- ↑ "Investigation of superluminescence emitted by a gallium arsenide diode" (in en). https://www.researchgate.net/publication/284509143.
- ↑ 3.0 3.1 Miller, S. E.; Li, Tingye; Marcatili, E. A. J. (1973). "Part II: Devices and systems considerations". Proceedings of the IEEE 61 (12): 1726–1751. doi:10.1109/PROC.1973.9362. ISSN 0018-9219.
- ↑ Lee, Tien-Pei; Burrus, C.; Miller, B. (1973). "A stripe-geometry double-heterostructure amplified-spontaneous-emission (superluminescent) diode". IEEE Journal of Quantum Electronics 9 (8): 820–828. doi:10.1109/JQE.1973.1077738. ISSN 0018-9197.
- ↑ Alphonse, G. A.; Gilbert, D. B.; Harvey, M. G.; Ettenberg, M. (1988). "High-power superluminescent diodes". IEEE Journal of Quantum Electronics 24 (12): 2454–2457. doi:10.1109/3.14376. ISSN 0018-9197.
External links
- Encyclopedia of Laser Physics and Technology entry
- Short overview of device operation principles and performance parameters (PDF).
 |