Physics:Alfvén's theorem
In ideal magnetohydrodynamics, Alfvén's theorem, or the frozen-in flux theorem, states that electrically conducting fluids and embedded magnetic fields are constrained to move together in the limit of large magnetic Reynolds numbers. It is named after Hannes Alfvén, who put the idea forward in 1943.
Alfvén's theorem implies that the magnetic topology of a fluid in the limit of a large magnetic Reynolds number cannot change. This approximation breaks down in current sheets, where magnetic reconnection can occur.
History
The concept of magnetic fields being frozen into fluids with infinite electrical conductivity was first proposed by Hannes Alfvén in a 1943 paper titled "On the Existence of Electromagnetic-Hydrodynamic Waves" published in the journal Arkiv för matematik, astronomi och fysik. He wrote:[1]
In view of the infinite conductivity, every motion (perpendicular to the field) of the liquid in relation to the lines of force is forbidden because it would give infinite eddy currents. Thus the matter of the liquid is "fastened" to the lines of force...
"On the Existence of Electromagnetic-Hydrodynamic Waves" interpreted the results of Alfvén's earlier paper "Existence of Electromagnetic-Hydrodynamic Waves" published in the journal Nature in 1942.[2]
Later in life, Alfvén advised against the use of his own theorem.[3]
Overview
Informally, Alfvén's theorem refers to the fundamental result in ideal magnetohydrodynamic theory that electrically conducting fluids and the magnetic fields within are constrained to move together in the limit of large magnetic Reynolds numbers (Rm)—such as when the fluid is a perfect conductor or when velocity and length scales are infinitely large. Motions of the two are constrained in that all bulk fluid motions perpendicular to the magnetic field result in matching perpendicular motion of the field at the same velocity and vice versa.
Formally, the connection between the movement of the fluid and the movement of the magnetic field is detailed in two primary results, often referred to as magnetic flux conservation and magnetic field line conservation. Magnetic flux conservation implies that the magnetic flux through a surface moving with the bulk fluid velocity is constant, and magnetic field line conservation implies that, if two fluid elements are connected by a magnetic field line, they will always be.[4]
Flux tubes and field lines
Alfvén's theorem is frequently expressed in terms of magnetic flux tubes and magnetic field lines.
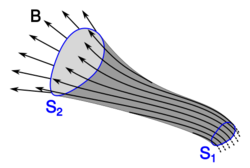
A magnetic flux tube is a tube- or cylinder-like region of space containing a magnetic field such that its sides are everywhere parallel to the field. Consequently, the magnetic flux through these sides is zero, and the cross-sections along the tube's length have constant, equal magnetic flux. In the limit of a large magnetic Reynolds number, Alfvén's theorem requires that these surfaces of constant flux move with the fluid that they are embedded in. As such, magnetic flux tubes are frozen into the fluid.
The intersection of the sides of two magnetic flux tubes form a magnetic field line, a curve that is everywhere parallel to the magnetic field. In fluids where flux tubes are frozen-in, it then follows that magnetic field lines must also be frozen-in. However, the conditions for frozen-in field lines are weaker than the conditions for frozen-in flux tubes, or, equivalently, for conservation of flux.[5]:25
Mathematical statement
In mathematical terms, Alfvén's theorem states that, in an electrically conducting fluid in the limit of a large magnetic Reynolds number, the magnetic flux ΦB through an orientable, open material surface advected by a macroscopic, space- and time-dependent velocity field[note 1] v is constant, or
- [math]\displaystyle{ \frac{D\Phi_B}{Dt} = 0 , }[/math]
where D/Dt = ∂/∂t + (v ⋅ ∇) is the advective derivative.
Flux conservation
In ideal magnetohydrodynamics, magnetic induction dominates over magnetic diffusion at the velocity and length scales being studied. The diffusion term in the governing induction equation is then assumed to be small relative to the induction term and is neglected. The induction equation then reduces to its ideal form:
- [math]\displaystyle{ \frac{\partial\mathbf{B}}{\partial t} = \nabla \times \left(\mathbf{v}\times\mathbf{B}\right). }[/math]
The conservation of magnetic flux through material surfaces embedded in the fluid follows directly from the ideal induction equation and the assumption of no magnetic monopoles through Gauss's law for magnetism.[6][7]
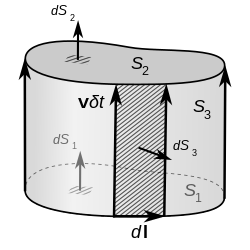
In an electrically conducting fluid with a space- and time-dependent magnetic field B and velocity field v, an arbitrary, orientable, open surface S1 at time t is advected by v in a small time δt to the surface S2. The rate of change of the magnetic flux through the surface as it is advected from S1 to S2 is then
- [math]\displaystyle{ \frac{D\Phi_B}{Dt} = \lim_{\delta t \to 0} \frac{\iint_{S_2} \mathbf{B}(t+\delta t) \cdot d\mathbf{S}_2 - \iint_{S_1} \mathbf{B}(t) \cdot d\mathbf{S}_1}{\delta t}. }[/math]
The surface integral over S2 can be re expressed by applying Gauss's law for magnetism to assume that the magnetic flux through a closed surface formed by S1, S2, and the surface S3 that connects the boundaries of S1 and S2 is zero. At time t + δt, this relationship can be expressed as
- [math]\displaystyle{ 0 = -\iint_{S_1} \mathbf{B}(t+\delta t)\cdot d\mathbf{S}_1 + \iint_{S_2} \mathbf{B}(t+\delta t)\cdot d\mathbf{S}_2 + \iint_{S_3} \mathbf{B}(t+\delta t)\cdot d\mathbf{S}_3 , }[/math]
where the sense of S1 was reversed so that dS1 points outwards from the enclosed volume. In the surface integral over S3, the differential surface element dS3 = dl × v δt where dl is the line element around the boundary ∂S1 of the surface S1. Solving for the surface integral over S2 then gives
- [math]\displaystyle{ \iint_{S_2} \mathbf{B}(t+\delta t)\cdot d\mathbf{S}_2 = \iint_{S_1} \mathbf{B}(t+\delta t)\cdot d\mathbf{S}_1 - \oint_{\partial S_1} \left(\mathbf{v}\ \delta t \times \mathbf{B}(t)\right) \cdot d\mathbf{l}, }[/math]
where the final term was rewritten using the properties of scalar triple products and a first-order approximation was taken. Substituting this into the expression for DΦB/Dt and simplifying results in
- [math]\displaystyle{ \begin{align} \frac{D\Phi_B}{Dt} = \lim_{\delta t \to 0} \iint_{S_1} \frac{\mathbf{B}(t+\delta t) - \mathbf{B}(t)}{\delta t} \cdot d\mathbf{S}_1 - \oint_{\partial S_1} \left(\mathbf{v} \times \mathbf{B}(t)\right) \cdot d\mathbf{l}. \end{align} }[/math]
Applying the definition of a partial derivative to the integrand of the first term, applying Stokes' theorem to the second term, and combining the resultant surface integrals gives
- [math]\displaystyle{ \frac{D\Phi_B}{Dt} = \iint_{S_1} \left( \frac{\partial\mathbf{B}}{\partial t} - \nabla\times\left(\mathbf{v} \times \mathbf{B}\right) \right) \cdot d\mathbf{S}_1. }[/math]
Using the ideal induction equation, the integrand vanishes, and
- [math]\displaystyle{ \frac{D\Phi_B}{Dt} = 0. }[/math]
Field line conservation
Field line conservation can also be derived mathematically using the ideal induction equation, Gauss's law for magnetism, and the mass continuity equation.[5]
The ideal induction equation can be rewritten using a vector identity and Gauss's law for magnetism as
- [math]\displaystyle{ \frac{\partial\mathbf{B}}{\partial t} = (\mathbf{B}\cdot\nabla)\mathbf{v} - (\mathbf{v}\cdot\nabla)\mathbf{B} - \mathbf{B}(\nabla\cdot\mathbf{v}). }[/math]
Using the mass continuity equation,
- [math]\displaystyle{ \frac{\partial\rho}{\partial t} + (\mathbf{v}\cdot\nabla)\rho = -\rho\nabla\cdot\mathbf{v}, }[/math]
the ideal induction equation can be further rearranged to give
- [math]\displaystyle{ \frac{D}{Dt} \left(\frac{\mathbf{B}}{\rho}\right) = \left(\frac{\mathbf{B}}{\rho}\cdot\nabla\right)\mathbf{v}. }[/math]
Similarly, for a line segment δl where v is the bulk plasma velocity at one end and v + δv is the velocity at the other end, the differential velocity between the two ends is δv = (δl ⋅ ∇)v and
- [math]\displaystyle{ \frac{D\delta\mathbf{l}}{Dt} = (\delta\mathbf{l}\cdot\nabla)\mathbf{v} }[/math],
which has the same form as the equation obtained previously for B/ρ. Therefore, if δl and B are initially parallel, they will remain parallel.
While flux conservation implies field line conservation (see § Flux tubes and field lines), the conditions for the latter are weaker than the conditions for the former. Unlike the conditions for flux conservation, the conditions for field line conservation can be satisfied when an additional, source term parallel to the magnetic field is present in the ideal induction equation.
Mathematically, for field lines to be frozen-in, the fluid must satisfy
- [math]\displaystyle{ \left( \frac{\partial\mathbf{B}}{\partial t} - \nabla \times \left(\mathbf{v}\times\mathbf{B}\right)\right) \times \mathbf{B} = 0, }[/math]
whereas, for flux to be conserved, the fluid must satisfy the stronger condition imposed by the ideal induction equation.[8][9]
Kelvin's circulation theorem
Kelvin's circulation theorem states that vortex tubes moving with an ideal fluid are frozen to the fluid, analogous to how magnetic flux tubes moving with a perfectly conducting ideal-MHD fluid are frozen to the fluid. The ideal induction equation takes the same form as the equation for vorticity ω = ∇ × v in an ideal fluid where v is the velocity field:
- [math]\displaystyle{ \frac{\partial \boldsymbol{\omega}}{\partial t} = \nabla \times (\mathbf{v}\times\boldsymbol{\omega}). }[/math]
However, the induction equation is linear, whereas there is a nonlinear relationship between ∇ × v and v in the vorticity equation.[9]
Implications
Alfvén's theorem indicates that the magnetic field topology cannot change in a perfectly conducting fluid. However, in the case of complicated or turbulent flows, this would lead to highly tangled magnetic fields with very complicated topologies that should impede the fluid motions. Astrophysical plasmas with high electrical conductivities do not generally show such complicated tangled fields. Magnetic reconnection seems to occur in these plasmas unlike what would be expected from the flux freezing conditions. This has important implications for magnetic dynamos. In fact, a very high electrical conductivity translates into high magnetic Reynolds numbers, which indicates that the plasma will be turbulent.[10]
Resistive fluids
Even for the non-ideal case, in which the electric conductivity is not infinite, a similar result can be obtained by defining the magnetic flux transporting velocity by writing:
- [math]\displaystyle{ \nabla \times (\bf{w}\times \bf{B})=\eta \nabla^2 \bf{B} + \nabla \times (\bf{v} \times \bf{B}), }[/math]
in which, instead of fluid velocity, v, the flux velocity w has been used. Although, in some cases, this velocity field can be found using magnetohydrodynamic equations, the existence and uniqueness of this vector field depends on the underlying conditions.[11]
Stochastic flux freezing
The conventional views on flux freezing in highly conducting plasmas are inconsistent with the phenomenon of spontaneous stochasticity. Unfortunately, it has become a standard argument, even in textbooks, that magnetic flux freezing should hold increasingly better as magnetic diffusivity tends to zero (non-dissipative regime). But the subtlety is that very large magnetic Reynolds numbers (i.e., small electric resistivity or high electrical conductivities) are usually associated with high kinetic Reynolds numbers (i.e., very small viscosities). If kinematic viscosity tends to zero simultaneously with the resistivity, and if the plasma becomes turbulent (associated with high Reynolds numbers), then Lagrangian trajectories will no longer be unique. The conventional "naïve" flux freezing argument, discussed above, does not apply in general, and stochastic flux freezing must be employed.[12]
The stochastic flux-freezing theorem for resistive magnetohydrodynamics generalizes ordinary flux-freezing discussed above. This generalized theorem states that magnetic field lines of the fine-grained magnetic field B are "frozen-in" to the stochastic trajectories solving the following stochastic differential equation, known as the Langevin equation:
- [math]\displaystyle{ d{\bf{x}}={\bf{u}}({\bf{x}},t)dt+\sqrt{2\eta} d{\bf{W}}(t) }[/math]
in which η is magnetic diffusivity and W is the three-dimensional Gaussian white noise (see also Wiener process.) The many "virtual" field-vectors that arrive at the same final point must be averaged to obtain the physical magnetic field at that point.[13]
See also
Explanatory notes
- ↑ In magnetohydrodynamics (MHD), the bulk velocity field v is a linear combination of the mean motions of the individual species weighted by the species' respective mass. Under Alfvén's theorem, the magnetic field is restricted to move with this bulk velocity, but not necessarily with the velocity of the individual species. As such, Alfvén's theorem does not guarantee that individual species within the fluid will be restricted to move with the magnetic field, and currents can flow perpendicular to the magnetic field provided the bulk velocity matches the velocity of the magnetic field.[citation needed]
References
- ↑ Alfvén, Hannes (1943). "On the Existence of Electromagnetic-Hydrodynamic Waves". Arkiv för matematik, astronomi och fysik 29B(2): 1–7. https://archive.org/download/MagnetohydrodynamicWavesAlfven1943/Magnetohydrodynamic%20waves%20-%20Alfven%201943.pdf.
- ↑ Alfvén, Hannes (1942). "Existence of Electromagnetic-Hydrodynamic Waves". Nature 150 (3805): 405. doi:10.1038/150405d0. Bibcode: 1942Natur.150..405A.
- ↑ Alfvén, H. (August 1976). "On frozen-in field lines and field-line reconnection" (in en). Journal of Geophysical Research 81 (22): 4019–4021. doi:10.1029/JA081i022p04019. Bibcode: 1976JGR....81.4019A. https://doi.org/10.1029/JA081i022p04019.
- ↑ Priest, E. (2016). "MHD Structures in Three-Dimensional Reconnection". Magnetic Reconnection. Astrophysics and Space Science Library. 427. pp. 101–142. doi:10.1007/978-3-319-26432-5_3. ISBN 978-3-319-26430-1.
- ↑ 5.0 5.1 Priest, Eric; Forbes, Terry (2000). Magnetic Reconnection: MHD Theory and Applications (First ed.). Cambridge University Press. ISBN 0-521-48179-1.
- ↑ Blackman, Eric G (1 March 2013). "On deriving flux freezing in magnetohydrodynamics by direct differentiation". European Journal of Physics 34 (2): 489–494. doi:10.1088/0143-0807/34/2/489. Bibcode: 2013EJPh...34..489B.
- ↑ Lyu, Ling-Hsiao (2010). Elementary Space Plasma Physics. Taipei: Airiti Press Inc. pp. 173–176. ISBN 978-9868270954. http://www.ss.ncu.edu.tw/~lyu/lecture_files_en/lyu_SPP_Book_A4format_pdf_html/pdf_2_App/lyu_SPP_Appendix_C.pdf. Retrieved 12 January 2023.
- ↑ Eyink, Gregory L.; Aluie, Hussein (November 2006). "The breakdown of Alfvén's theorem in ideal plasma flows: Necessary conditions and physical conjectures". Physica D: Nonlinear Phenomena 223 (1): 82–92. doi:10.1016/j.physd.2006.08.009. Bibcode: 2006PhyD..223...82E.
- ↑ 9.0 9.1 Gubbins, David; Herrero-Bervera, Emilio, eds (2007). Encyclopedia of Geomagnetism and Paleomagnetism. Dordrecht: Springer. pp. 7–11. doi:10.1007/978-1-4020-4423-6. ISBN 978-1-4020-3992-8. https://link.springer.com/referencework/10.1007/978-1-4020-4423-6.
- ↑ Eyink, Gregory; Aluie, Hussein (2006). "The breakdown of Alfvén's theorem in ideal plasma flows: Necessary conditions and physical conjectures". Physica D: Nonlinear Phenomena 223 (1): 82. doi:10.1016/j.physd.2006.08.009. Bibcode: 2006PhyD..223...82E.
- ↑ Wilmot-Smith, A. L.; Priest, E. R.; Horing, G. (2005). "Magnetic diffusion and the motion of field lines". Geophysical & Astrophysical Fluid Dynamics 99 (2): 177–197. doi:10.1080/03091920500044808. Bibcode: 2005GApFD..99..177W.
- ↑ Eyink, Gregory (2011). "Stochastic flux freezing and magnetic dynamo". Physical Review E 83 (5): 056405. doi:10.1103/PhysRevE.83.056405. PMID 21728673. Bibcode: 2011PhRvE..83e6405E.
- ↑ Lalescu, Cristian C.; Shi, Yi-Kang; Eyink, Gregory; Drivas, Theodore D.; Vishniac, Ethan; Lazarian, Alex (2015). "Inertial-Range Reconnection in Magnetohydrodynamic Turbulence and in the Solar Wind". Physical Review Letters 115 (2): 025001. doi:10.1103/PhysRevLett.115.025001. PMID 26207472. Bibcode: 2015PhRvL.115b5001L.
 |