Physics:Eddy current
| Part of a series of articles about |
| Electromagnetism |
|---|
 |
In electromagnetism, an eddy current (also called Foucault's current) is a loop of electric current induced within conductors by a changing magnetic field in the conductor according to Faraday's law of induction or by the relative motion of a conductor in a magnetic field. Eddy currents flow in closed loops within conductors, in planes perpendicular to the magnetic field. They can be induced within nearby stationary conductors by a time-varying magnetic field created by an AC electromagnet or transformer, for example, or by relative motion between a magnet and a nearby conductor. The magnitude of the current in a given loop is proportional to the strength of the magnetic field, the area of the loop, and the rate of change of flux, and inversely proportional to the resistivity of the material. When graphed, these circular currents within a piece of metal look vaguely like eddies or whirlpools in a liquid.
By Lenz's law, an eddy current creates a magnetic field that opposes the change in the magnetic field that created it, and thus eddy currents react back on the source of the magnetic field. For example, a nearby conductive surface will exert a drag force on a moving magnet that opposes its motion, due to eddy currents induced in the surface by the moving magnetic field. This effect is employed in eddy current brakes which are used to stop rotating power tools quickly when they are turned off. The current flowing through the resistance of the conductor also dissipates energy as heat in the material. Thus eddy currents are a cause of energy loss in alternating current (AC) inductors, transformers, electric motors and generators, and other AC machinery, requiring special construction such as laminated magnetic cores or ferrite cores to minimize them. Eddy currents are also used to heat objects in induction heating furnaces and equipment, and to detect cracks and flaws in metal parts using eddy-current testing instruments.
Origin of term
The term eddy current comes from analogous currents seen in water in fluid dynamics, causing localised areas of turbulence known as eddies giving rise to persistent vortices. Somewhat analogously, eddy currents can take time to build up and can persist for very long times in conductors due to their inductance.
History
The first person to observe eddy currents was François Arago (1786–1853), the 25th Prime Minister of France, who was also a mathematician, physicist and astronomer. In 1824 he observed what has been called rotatory magnetism, and that most conductive bodies could be magnetized; these discoveries were completed and explained by Michael Faraday (1791–1867).
In 1834, Emil Lenz stated Lenz's law, which says that the direction of induced current flow in an object will be such that its magnetic field will oppose the change of magnetic flux that caused the current flow. Eddy currents produce a secondary field that cancels a part of the external field and causes some of the external flux to avoid the conductor.
French physicist Léon Foucault (1819–1868) is credited with having discovered eddy currents. In September 1855, he discovered that the force required for the rotation of a copper disc becomes greater when it is made to rotate with its rim between the poles of a magnet, the disc at the same time becoming heated by the eddy current induced in the metal. The first use of eddy current for non-destructive testing occurred in 1879 when David E. Hughes used the principles to conduct metallurgical sorting tests.
Explanation
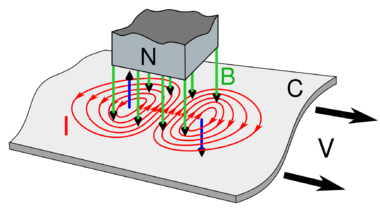
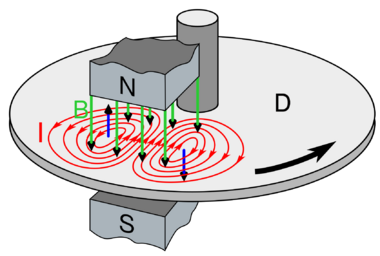
A magnet induces circular electric currents in a metal sheet moving through its magnetic field. See the diagram at right. It shows a metal sheet (C) moving to the right with velocity v under a stationary magnet. The magnetic field (B, green arrows) of the magnet's north pole N passes down through the sheet. Since the metal is moving, the magnetic flux through a given area of the sheet is changing. In the part of the sheet moving under the leading edge of the magnet (left side) the magnetic field through a given point on the sheet is increasing as it gets nearer the magnet, dB/dt > 0. From Faraday's law of induction, this creates a circular electric field in the sheet in a counterclockwise direction around the magnetic field lines. This field induces a counterclockwise flow of electric current (I, red), in the sheet. This is the eddy current. In the part of the sheet under the trailing edge of the magnet (right side) the magnetic field through a given point on the sheet is decreasing as it is moving further away from the magnet, dB/dt < 0, inducing a second eddy current in a clockwise direction in the sheet.
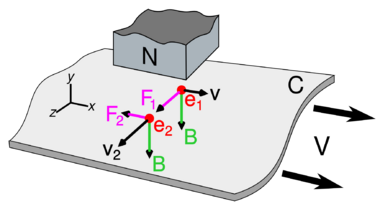
Another equivalent way to understand the current is to see that the free charge carriers (electrons) in the metal sheet are moving with the sheet to the right, so the magnetic field exerts a sideways force on them due to the Lorentz force. Since the velocity v of the charges is to the right and the magnetic field B is directed down, from the right hand rule the Lorentz force on positive charges F = q(v × B) is toward the rear of the diagram (to the left when facing in the direction of motion v). This causes a current I toward the rear under the magnet, which circles around through parts of the sheet outside the magnetic field, clockwise to the right and counterclockwise to the left, to the front of the magnet again. The mobile charge carriers in the metal, the electrons, actually have a negative charge (q < 0) so their motion is opposite in direction to the conventional current shown.
The magnetic field of the magnet, acting on the electrons moving sideways under the magnet, then exerts a Lorentz force directed to the rear, opposite to the velocity of the metal sheet. The electrons, in collisions with the metal lattice atoms, transfer this force to the sheet, exerting a drag force on the sheet proportional to its velocity. The kinetic energy which is consumed overcoming this drag force is dissipated as heat by the currents flowing through the resistance of the metal, so the metal gets warm under the magnet.
Due to Ampère's circuital law each of the circular currents in the sheet creates a counter magnetic field (blue arrows). Another way to understand the drag force is to see that due to Lenz's law the counterfields oppose the change in magnetic field through the sheet. At the leading edge of the magnet (left side) by the right hand rule the counterclockwise current creates a magnetic field pointed up, opposing the magnet's field, causing a repulsive force between the sheet and the leading edge of the magnet. In contrast, at the trailing edge (right side), the clockwise current causes a magnetic field pointed down, in the same direction as the magnet's field, creating an attractive force between the sheet and the trailing edge of the magnet. Both of these forces oppose the motion of the sheet.
Properties
Eddy currents in conductors of non-zero resistivity generate heat as well as electromagnetic forces. The heat can be used for induction heating. The electromagnetic forces can be used for levitation, creating movement, or to give a strong braking effect. Eddy currents can also have undesirable effects, for instance power loss in transformers. In this application, they are minimized with thin plates, by lamination of conductors or other details of conductor shape.
Self-induced eddy currents are responsible for the skin effect in conductors.[1] The latter can be used for non-destructive testing of materials for geometry features, like micro-cracks.[2] A similar effect is the proximity effect, which is caused by externally induced eddy currents.[3]
An object or part of an object experiences steady field intensity and direction where there is still relative motion of the field and the object (for example in the center of the field in the diagram), or unsteady fields where the currents cannot circulate due to the geometry of the conductor. In these situations charges collect on or within the object and these charges then produce static electric potentials that oppose any further current. Currents may be initially associated with the creation of static potentials, but these may be transitory and small.
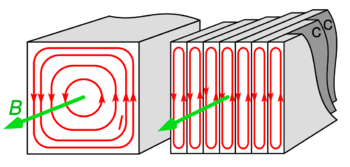
Eddy currents generate resistive losses that transform some forms of energy, such as kinetic energy, into heat. This Joule heating reduces efficiency of iron-core transformers and electric motors and other devices that use changing magnetic fields. Eddy currents are minimized in these devices by selecting magnetic core materials that have low electrical conductivity (e.g., ferrites) or by using thin sheets of magnetic material, known as laminations. Electrons cannot cross the insulating gap between the laminations and so are unable to circulate on wide arcs. Charges gather at the lamination boundaries, in a process analogous to the Hall effect, producing electric fields that oppose any further accumulation of charge and hence suppressing the eddy currents. The shorter the distance between adjacent laminations (i.e., the greater the number of laminations per unit area, perpendicular to the applied field), the greater the suppression of eddy currents.
The conversion of input energy to heat is not always undesirable, however, as there are some practical applications. One is in the brakes of some trains known as eddy current brakes. During braking, the metal wheels are exposed to a magnetic field from an electromagnet, generating eddy currents in the wheels. This eddy current is formed by the movement of the wheels. So, by Lenz's law, the magnetic field formed by the eddy current will oppose its cause. Thus the wheel will face a force opposing the initial movement of the wheel. The faster the wheels are spinning, the stronger the effect, meaning that as the train slows the braking force is reduced, producing a smooth stopping motion.
Induction heating makes use of eddy currents to provide heating of metal objects.
Power dissipation of eddy currents
Under certain assumptions (uniform material, uniform magnetic field, no skin effect, etc.) the power lost due to eddy currents per unit mass for a thin sheet or wire can be calculated from the following equation:[4] [math]\displaystyle{ P = \frac{\pi^2 {B_\text{p}}^2 d^2 f^2 }{6k \rho D}, }[/math] where
- P is the power lost per unit mass (W/kg),
- Bp is the peak magnetic field (T),
- d is the thickness of the sheet or diameter of the wire (m),
- f is the frequency (Hz),
- k is a constant equal to 1 for a thin sheet and 2 for a thin wire,
- ρ is the resistivity of the material (Ω m), and
- D is the density of the material (kg/m3).
This equation is valid only under the so-called quasi-static conditions, where the frequency of magnetisation does not result in the skin effect; that is, the electromagnetic wave fully penetrates the material.
Skin effect
In very fast-changing fields, the magnetic field does not penetrate completely into the interior of the material. This skin effect renders the above equation invalid. However, in any case increased frequency of the same value of field will always increase eddy currents, even with non-uniform field penetration.[citation needed]
The penetration depth for a good conductor can be calculated from the following equation:[5] [math]\displaystyle{ \delta = \frac{1}\sqrt{\pi f \mu \sigma}, }[/math] where δ is the penetration depth (m), f is the frequency (Hz), μ is the magnetic permeability of the material (H/m), and σ is the electrical conductivity of the material (S/m).
Diffusion equation
The derivation of a useful equation for modelling the effect of eddy currents in a material starts with the differential, magnetostatic form of Ampère's Law,[6] providing an expression for the magnetizing field H surrounding a current density J: [math]\displaystyle{ \nabla \times \mathbf{H} = \mathbf{J}. }[/math]
Taking the curl on both sides of this equation and then using a common vector calculus identity for the curl of the curl results in [math]\displaystyle{ \nabla \left( \nabla \cdot \mathbf{H} \right) - \nabla^2\mathbf{H} = \nabla \times \mathbf{J}. }[/math]
From Gauss's law for magnetism, ∇ ⋅ H = 0, so [math]\displaystyle{ -\nabla^2\mathbf{H}=\nabla\times\mathbf{J}. }[/math]
Using Ohm's law, J = σE, which relates current density J to electric field E in terms of a material's conductivity σ, and assuming isotropic homogeneous conductivity, the equation can be written as [math]\displaystyle{ -\nabla^2\mathbf{H}=\sigma\nabla\times\mathbf{E}. }[/math]
Using the differential form of Faraday's law, ∇ × E = −∂B/∂t, this gives [math]\displaystyle{ \nabla^2\mathbf{H} = \sigma \frac{\partial \mathbf{B}}{\partial t}. }[/math]
By definition, B = μ0(H + M), where M is the magnetization of the material and μ0 is the vacuum permeability. The diffusion equation therefore is [math]\displaystyle{ \nabla^2\mathbf{H} = \mu_0 \sigma \left( \frac{\partial \mathbf{M} }{\partial t} + \frac{\partial \mathbf{H}}{\partial t} \right). }[/math]
Applications
Electromagnetic braking
File:20. Валтенхофеново правило.ogv
Eddy current brakes use the drag force created by eddy currents as a brake to slow or stop moving objects. Since there is no contact with a brake shoe or drum, there is no mechanical wear. However, an eddy current brake cannot provide a "holding" torque and so may be used in combination with mechanical brakes, for example, on overhead cranes. Another application is on some roller coasters, where heavy copper plates extending from the car are moved between pairs of very strong permanent magnets. Electrical resistance within the plates causes a dragging effect analogous to friction, which dissipates the kinetic energy of the car. The same technique is used in electromagnetic brakes in railroad cars and to quickly stop the blades in power tools such as circular saws. Using electromagnets, as opposed to permanent magnets, the strength of the magnetic field can be adjusted and so the magnitude of braking effect changed.
Repulsive effects and levitation
In a varying magnetic field, the induced currents exhibit diamagnetic-like repulsion effects. A conductive object will experience a repulsion force. This can lift objects against gravity, though with continual power input to replace the energy dissipated by the eddy currents. An example application is separation of aluminum cans from other metals in an eddy current separator. Ferrous metals cling to the magnet, and aluminum (and other non-ferrous conductors) are forced away from the magnet; this can separate a waste stream into ferrous and non-ferrous scrap metal.
With a very strong handheld magnet, such as those made from neodymium, one can easily observe a very similar effect by rapidly sweeping the magnet over a coin with only a small separation. Depending on the strength of the magnet, identity of the coin, and separation between the magnet and coin, one may induce the coin to be pushed slightly ahead of the magnet – even if the coin contains no magnetic elements, such as the US penny. Another example involves dropping a strong magnet down a tube of copper[7] – the magnet falls at a dramatically slow pace.
In a perfect conductor with no resistance, surface eddy currents exactly cancel the field inside the conductor, so no magnetic field penetrates the conductor. Since no energy is lost in resistance, eddy currents created when a magnet is brought near the conductor persist even after the magnet is stationary, and can exactly balance the force of gravity, allowing magnetic levitation. Superconductors also exhibit a separate inherently quantum mechanical phenomenon called the Meissner effect in which any magnetic field lines present in the material when it becomes superconducting are expelled, thus the magnetic field in a superconductor is always zero.
Using electromagnets with electronic switching comparable to electronic speed control it is possible to generate electromagnetic fields moving in an arbitrary direction. As described in the section above about eddy current brakes, a non-ferromagnetic conductor surface tends to rest within this moving field. When however this field is moving, a vehicle can be levitated and propelled. This is comparable to a maglev but is not bound to a rail.[8]
Identification of metals
In some coin-operated vending machines, eddy currents are used to detect counterfeit coins, or slugs. The coin rolls past a stationary magnet, and eddy currents slow its speed. The strength of the eddy currents, and thus the retardation, depends on the conductivity of the coin's metal. Slugs are slowed to a different degree than genuine coins, and this is used to send them into the rejection slot.
Vibration and position sensing
Eddy currents are used in certain types of proximity sensors to observe the vibration and position of rotating shafts within their bearings. This technology was originally pioneered in the 1930s by researchers at General Electric using vacuum tube circuitry. In the late 1950s, solid-state versions were developed by Donald E. Bently at Bently Nevada Corporation. These sensors are extremely sensitive to very small displacements making them well suited to observe the minute vibrations (on the order of several thousandths of an inch) in modern turbomachinery. A typical proximity sensor used for vibration monitoring has a scale factor of 200 mV/mil.[clarification needed] Widespread use of such sensors in turbomachinery has led to development of industry standards that prescribe their use and application. Examples of such standards are American Petroleum Institute (API) Standard 670 and ISO 7919.
A Ferraris acceleration sensor, also called a Ferraris sensor, is a contactless sensor that uses eddy currents to measure relative acceleration.[9][10][11]
Structural testing
Eddy current techniques are commonly used for the nondestructive examination (NDE) and condition monitoring of a large variety of metallic structures, including heat exchanger tubes, aircraft fuselage, and aircraft structural components.
Skin effects
Eddy currents are the root cause of the skin effect in conductors carrying alternating current.
Similarly, in magnetic materials of finite conductivity, eddy currents cause the confinement of the majority of the magnetic fields to only a couple skin depths of the surface of the material. This effect limits the flux linkage in inductors and transformers having magnetic cores.
Other applications
- Rock climbing auto belays[12]
- Zip line brakes[13]
- Free fall devices[14]
- Metal detectors
- Conductivity meters for non-magnetic metals[15][16]
- Eddy current adjustable-speed drives
- Eddy-current testing
- Eddy current brake
- Electricity meters (electromechanical induction meters)
- Induction heating
- Cooking (induction stovetops)
- Proximity sensor (displacement sensors)
- Vending machines (detection of coins)
- Coating thickness measurements[17]
- Sheet resistance measurement[18]
- Eddy current separator for metal separation[19]
- Mechanical speedometers
- Safety hazard and defect detection applications
- Magnetic damping
References
- Online citations
- ↑ Israel D. Vagner; B.I. Lembrikov; Peter Rudolf Wyder (17 November 2003). Electrodynamics of Magnetoactive Media. Springer Science & Business Media. pp. 73–. ISBN 978-3-540-43694-2. https://books.google.com/books?id=E8caSplsF28C&pg=PA73.
- ↑ Walt Boyes (25 November 2009). Instrumentation Reference Book. Butterworth-Heinemann. pp. 570–. ISBN 978-0-08-094188-2. https://books.google.com/books?id=ZvscLzOlkNgC&pg=PA570.
- ↑ Howard Johnson; Howard W. Johnson; Martin Graham (2003). High-speed Signal Propagation: Advanced Black Magic. Prentice Hall Professional. pp. 80–. ISBN 978-0-13-084408-8. https://books.google.com/books?id=mMJxcWqm_1oC&pg=PA80.
- ↑ F. Fiorillo, Measurement and Characterization of Magnetic Materials, Elsevier Academic Press, 2004, ISBN:0-12-257251-3, page. 31
- ↑ Wangsness, Roald. Electromagnetic Fields (2nd ed.). pp. 387–8.
- ↑ G. Hysteresis in Magnetism: For Physicists, Materials Scientists, and Engineers, San Diego: Academic Press, 1998.
- ↑ Archived at Ghostarchive and the Wayback Machine: "Eddy Current Tubes". https://www.youtube.com/watch?v=nrw-i5Ku0mI.
- ↑ Hendo Hoverboards - World's first REAL hoverboard
- ↑ Bernhard Hiller. "Ferraris Acceleration Sensor - Principle and Field of Application in Servo Drives" .
- ↑ Jian Wang, Paul Vanherck, Jan Swevers, Hendrik Van Brussel. "Speed Observer Based on Sensor Fusion Combining Ferraris Sensor and Linear Position Encoder Signals".
- ↑ J. Fassnacht and P. Mutschler. "Benefits and limits of using an acceleration sensor in actively damping high frequent mechanical oscillations". 2001. doi: 10.1109/IAS.2001.955949 .
- ↑ "TRUBLUE Auto Belay". http://headrushtech.com/trublue-auto-belay/.
- ↑ "zipSTOP Zip Line Brake System". http://headrushtech.com/zipstop-zip-line-brake.
- ↑ "Our Patented Technology". http://headrushtech.com/about/technology.html.
- ↑ "Zappi - Eddy Current Conductivity Meter - Products". http://zappitec.com/en/products.php.
- ↑ "Institut Dr. Foerster: SIGMATEST". https://www.foerstergroup.de/en/deu/products/sigmatest-2069/.
- ↑ Coating Thickness Measurement with Electromagnetic Methods
- ↑ "Ohm/sq & OD". http://www.nagy-instruments.de/ohm_sq___od1.html.
- ↑ "Eddy Current Separator for metal separation". http://www.cogelme.com/eng/e-eddy-current-metal-separator.htm.
- General references
- Fitzgerald, A. E.; Kingsley, Charles Jr.; Umans, Stephen D. (1983). Electric Machinery (4th ed.). Mc-Graw-Hill, Inc.. p. 20. ISBN 978-0-07-021145-2. https://archive.org/details/electricmachifitz00fitz/page/20.
- Sears, Francis Weston; Zemansky, Mark W. (1955). University Physics (2nd ed.). Addison-Wesley. pp. 616–618. https://archive.org/details/universityphysic00searrich.
Further reading
- Stoll, R. L. (1974). The Analysis of Eddy Currents. Oxford University Press.
- Krawczyk, Andrzej; J. A. Tegopoulos. Numerical Modelling of Eddy Currents.
External links
- Eddy Current Separator Cogelme for non-ferrous metals separation – Information and video in Cogelme site
 |