Physics:Feshbach resonance

In physics, a Feshbach resonance can occur upon collision of two slow atoms, when they temporarily stick together forming an unstable compound with short lifetime (so-called resonance). It is a feature of many-body systems in which a bound state is achieved if the coupling(s) between at least one internal degree of freedom and the reaction coordinates, which lead to dissociation, vanish. The opposite situation, when a bound state is not formed, is a shape resonance. It is named after Herman Feshbach, a physicist at MIT.

Feshbach resonances have become important in the study of cold atoms systems, including Fermi gases and Bose–Einstein condensates (BECs). In the context of scattering processes in many-body systems, the Feshbach resonance occurs when the energy of a bound state of an interatomic potential is equal to the kinetic energy of a colliding pair of atoms. In experimental settings, the Feshbach resonances provide a way to vary interaction strength between atoms in the cloud by changing scattering length, a_sc, of elastic collisions. For atomic species that possess these resonances (like K³⁹ and K⁴⁰), it is possible to vary the interaction strength by applying a uniform magnetic field. Among many uses, this tool has served to explore the transition from a BEC of fermionic molecules to weakly interacting fermion-pairs the BCS in Fermi clouds. For the BECs, Feshbach resonances have been used to study a spectrum of systems from the non-interacting ideal Bose gases to the unitary regime of interactions.

Introduction

The interatomic potential of the open (red) and closed (blue) channel are shown. When the incoming energy of the free atoms, given by the dotted line, is approximately equivalent to that of the bound state in the closed channel, a temporary molecular state can form.

Consider a general quantum scattering event between two particles. In this reaction, there are two reactant particles denoted by A and B, and two product particles denoted by A' and B' . For the case of a reaction (such as a nuclear reaction), we may denote this scattering event by

[math]\displaystyle{ A + B \rightarrow A' + B' }[/math] or [math]\displaystyle{ A(B,B')A' }[/math].

The combination of the species and quantum states of the two reactant particles before or after the scattering event is referred to as a reaction channel. Specifically, the species and states of A and B constitute the entrance channel, while the types and states of A' and B' constitute the exit channel. An energetically accessible reaction channel is referred to as an open channel, whereas a reaction channel forbidden by energy conservation is referred to as a closed channel.

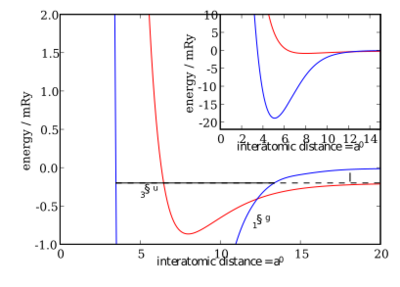
Consider the interaction of two particles A and B in an entrance channel C. The positions of these two particles are given by [math]\displaystyle{ \vec{r}_A }[/math] and [math]\displaystyle{ \vec{r}_B }[/math], respectively. The interaction energy of the two particles will usually depend only on the magnitude of the separation [math]\displaystyle{ R \equiv |\vec{r}_A - \vec{r}_B| }[/math], and this function, sometimes referred to as a potential energy curve, is denoted by [math]\displaystyle{ V_c(R) }[/math]. Often, this potential will have a pronounced minimum and thus admit bound states.

The total energy of the two particles in the entrance channel is

[math]\displaystyle{ E = T + V_c(R) + \Delta(\vec{P}) }[/math],

where [math]\displaystyle{ T }[/math] denotes the total kinetic energy of the relative motion (center-of-mass motion plays no role in the two-body interaction), [math]\displaystyle{ \Delta }[/math] is the contribution to the energy from couplings to external fields, and [math]\displaystyle{ \vec{P} }[/math] represents a vector of one or more parameters such as magnetic field or electric field. We consider now a second reaction channel, denoted by D, which is closed for large values of R. Let this potential curve [math]\displaystyle{ V_D(R) }[/math] admit a bound state with energy [math]\displaystyle{ E_D }[/math].

A Feshbach resonance occurs when

[math]\displaystyle{ E_D \approx T + V_c(R) + \Delta(\vec{P}_0) }[/math]

for some range of parameter vectors [math]\displaystyle{ \lbrace\vec{P}_0\rbrace }[/math]. When this condition is met, then any coupling between channel C and channel D can give rise to significant mixing between the two channels; this manifests itself as a drastic dependence of the outcome of the scattering event on the parameter or parameters that control the energy of the entrance channel. These couplings can arise from spin-exchange interactions or relativistic spin-dependent interactions.

Magnetic Feshbach resonance

In ultracold atomic experiments, the resonance is controlled via the magnetic field and we assume that the kinetic energy [math]\displaystyle{ T }[/math] is approximately 0. Since the channels differ in internal degrees of freedom such as spin and angular momentum, their difference in energy is dependent on [math]\displaystyle{ \vec{B} }[/math] by the Zeeman effect. The scattering length is modified as

[math]\displaystyle{ a=a_{bg}\left(1-\frac{\Delta}{B-B_0}\right) }[/math]

where [math]\displaystyle{ a_{bg} }[/math] is the background scattering length, [math]\displaystyle{ B_0 }[/math] is the magnetic field strength where resonance occurs, and [math]\displaystyle{ \Delta }[/math] is the resonance width. This allows for manipulation of the scattering length to 0 or arbitrarily high values.

As the magnetic field is swept through the resonance, the states in the open and closed channel can also mix and a large number of atoms, sometimes near 100% efficiency, convert to Feshbach molecules. These molecules have high vibrational states, so they then need to be transitioned to lower, more stable states to prevent dissociation. This can be done through stimulated emissions or other optical techniques such as STIRAP. Other methods include inducing stimulated emission through an oscillating magnetic field and atom-molecule thermalization.

Feshbach resonances in avoided crossings

In molecules, the nonadiabatic couplings between two adiabatic potentials build the avoided crossing (AC) region. The rovibronic resonances in the AC region of two-coupled potentials are very special, since they are not in the bound state region of the adiabatic potentials, and they usually do not play important roles on the scatterings and are less discussed. Yu Kun Yang et al studied this problem in the New J. Phys. 22 (2020). Exemplified in particle scattering, resonances in the AC region are comprehensively investigated. The effects of resonances in the AC region on the scattering cross sections strongly depend on the nonadiabatic couplings of the system, it can be very significant as sharp peaks, or inconspicuous buried in the background. More importantly, it shows a simple quantity proposed by Zhu and Nakamura to classify the coupling strength of nonadiabatic interactions, can be well applied to quantitatively estimate the importance of resonances in the AC region.

Unstable state

A virtual state, or unstable state is a bound or transient state which can decay into a free state or relax at some finite rate. This state may be the metastable state of a certain class of Feshbach resonance, "A special case of a Feshbach-type resonance occurs when the energy level lies near the very top of the potential well. Such a state is called 'virtual'" and may be further contrasted to a shape resonance depending on the angular momentum. Because of their transient existence, they can require special techniques for analysis and measurement, for example.

References

• R.J. Fletcher; A.L. Gaunt; N. Navon; R. Smith; Z. Hadzibabic (2013). "Stability of a Unitary Bose Gas". Phys. Rev. Lett. 111 (12): 125303. doi:10.1103/PhysRevLett.111.125303. PMID 24093273. Bibcode: 2013PhRvL.111l5303F. 
• Pethick; Smith (2002). Bose–Einstein Condensation in Dilute Gases. Cambridge. ISBN 0-521-66580-9. https://archive.org/details/boseeinsteincond0000peth. 
• Herman Feshbach (1958). "Unified theory of nuclear reactions". Annals of Physics 5 (4): 357. doi:10.1016/0003-4916(58)90007-1. Bibcode: 1958AnPhy...5..357F. 
• Fano, Ugo (1935). "Sullo spettro di assorbimento dei gas nobili presso il limite dello spettro d'arco" (in it). Il Nuovo Cimento (Springer Science and Business Media LLC) 12 (3): 154–161. doi:10.1007/bf02958288. ISSN 0029-6341. Bibcode: 1935NCim...12..154F. 
• Fano, U. (1961-12-15). "Effects of Configuration Interaction on Intensities and Phase Shifts". Physical Review (American Physical Society (APS)) 124 (6): 1866–1878. doi:10.1103/physrev.124.1866. ISSN 0031-899X. Bibcode: 1961PhRv..124.1866F. 
• Per-Olov Löwdin (1962). "Studies in Perturbation Theory. IV. Solution of Eigenvalue Problem by Projection Operator Formalism". J. Math. Phys. 3 (5): 969–982. doi:10.1063/1.1724312. Bibcode: 1962JMP.....3..969L. 
• Claude Bloch (1958). "Sur la théorie des perturbations des états liés". Nucl. Phys. 6: 329. doi:10.1016/0029-5582(58)90116-0. Bibcode: 1958NucPh...6..329B.