Physics:Flash freezing
In physics and chemistry, flash freezing is the process whereby objects are frozen in just a few hours[1] by subjecting them to cryogenic temperatures, or through direct contact with liquid nitrogen at −196 °C (−320.8 °F). It is commonly used in the food industry.
Flash freezing is of great importance in atmospheric science, as its study is necessary for a proper climate model for the formation of ice clouds in the upper troposphere, which effectively scatter incoming solar radiation and prevent Earth from becoming overheated by the sun.[2]
The process is also closely related to classical nucleation theory, which helps in understanding many materials, phenomena and theories in related situations.
Overview
When water is supercooled to temperatures below −48 °C (−54 °F), it must freeze.[3]
When water is in a conventional freezer, a dynamic phase transition is triggered.[4] The resulting ice depends on how quickly the system is cooled: if the water is cooled below its freezing point slowly, an ice crystal will result, rather than the poly-crystalline solid that flash freezing produces.[4]
Applications and techniques

Flash freezing is used in the food industry to quickly freeze perishable food items (see frozen food). In this case, food items are subjected to temperatures well below[clarification needed] the freezing point of water. Thus, smaller ice crystals are formed, causing less damage to cell membranes.[5]
Flash freezing techniques are used to freeze biological samples quickly so that large ice crystals cannot form and damage the sample.[6] This rapid freezing is done by submerging the sample in liquid nitrogen or a mixture of dry ice and ethanol.[7]
American inventor Clarence Birdseye developed the "quick-freezing" process of food preservation in the 20th century using a cryogenic process.[8] In practice, a mechanical freezing process is usually used due to cost instead. There have been continuous optimization of the freezing rate in mechanical freezing to minimize ice crystal size.[9]
The results have important implications in climate control research. One of the current debates is whether the formation of ice occurs near the surface or within the micrometre-sized droplets suspended in clouds. If it is the former, effective engineering approaches may be able to be taken to tune the surface tension of water so that the ice crystallization rate can be controlled.[2]
How water freezes
There are phenomena like supercooling, in which the water is cooled below its freezing point, but the water remains liquid, if there are too few defects to seed crystallization. One can therefore observe a delay until the water adjusts to the new, below-freezing temperature.[4] Supercooled liquid water must become ice at minus 48 C (minus 55 F) not just because of the extreme cold, but because the molecular structure of water changes physically to form tetrahedron shapes, with each water molecule loosely bonded to four others.[3] This suggests the structural change from liquid to "intermediate ice".[3] The crystallization of ice from supercooled water is generally initiated by a process called nucleation. The speed and size of nucleation occurs within nanoseconds and nanometers.[2]
The surface environment does not play a decisive role in the formation of ice and snow.[10] The density fluctuations inside drops result in that the possible freezing regions cover the middle and the surface regions.[11] The freezing from the surface or from within may be random.[11] However, in the strange world of water, tiny amounts of liquid water theoretically still are present, even as temperatures go below −48 °C (−54 °F) and almost all the water has turned solid, either into crystalline ice or amorphous water. Below −48 °C (−54 °F), ice is crystallizing too fast for any property of the remaining liquid to be measured.[3] The freezing speed directly influences the nucleation process and ice crystal size. A supercooled liquid will stay in a liquid state below the normal freezing point when it has little opportunity for nucleation; that is, if it is pure enough and has a smooth enough container. Once agitated it will rapidly become a solid. During the final stage of freezing, an ice drop develops a pointy tip, which is not observed for most other liquids, arises because water expands as it freezes.[10] Once the liquid is completely frozen, the sharp tip of the drop attracts water vapor in the air, much like a sharp metal lightning rod attracts electrical charges.[10] The water vapor collects on the tip and a tree of small ice crystals starts to grow.[10] An opposite effect has been shown to preferentially extract water molecules from the sharp edge of potato wedges in the oven.[10]
If a microscopic droplet of water is cooled very fast, it forms what is called a glass (low-density amorphous ice) in which all the tetrahedrons of water molecules are not lined up, but amorphous.[3] The change in structure of water controls the rate at which ice forms.[3] Depending on its temperature and pressure, water ice has 16 different crystalline forms in which water molecules cling to each other with hydrogen bonds.[3] When water is cooled, its structure becomes closer to the structure of ice, which is why the density goes down, and this should be reflected in an increased crystallization rate showing these crystalline forms.[3]
Related quantities
For the understanding of flash freezing, various related quantities might be useful.
Crystal growth or nucleation is the formation of a new thermodynamic phase or a new structure via self-assembly. Nucleation is often found to be very sensitive to impurities in the system. For nucleation of a new thermodynamic phase, such as the formation of ice in water below 0 °C (32 °F), if the system is not evolving with time and nucleation occurs in one step, then the probability that nucleation has not occurred should undergo exponential decay. This can also be observed in the nucleation of ice in supercooled small water droplets.[12] The decay rate of the exponential gives the nucleation rate and is given by
[math]\displaystyle{ R\ =\ N_S Zj\exp \left( \frac{-\Delta G^*}{k_BT} \right) }[/math]
Where
- [math]\displaystyle{ {\displaystyle \Delta G^{*}} }[/math] is the free energy cost of the nucleus at the top of the nucleation barrier, and kBT is the thermal energy with T the absolute temperature and kB is the Boltzmann constant.
- [math]\displaystyle{ {\displaystyle N_{S}} }[/math] is the number of nucleation sites.
- [math]\displaystyle{ {\displaystyle j} }[/math] is the rate at which molecules attach to the nucleus causing it to grow.
- [math]\displaystyle{ {\displaystyle Z} }[/math] is what is called the Zeldovich factor Z. Essentially the Zeldovich factor is the probability that a nucleus at the top of the barrier will go on to form the new phase, not dissolve.
Classical nucleation theory is a widely used approximate theory for estimating these rates, and how they vary with variables such as temperature. It correctly predicts that the time needed for nucleation decreases extremely rapidly when supersaturated.[13][14]
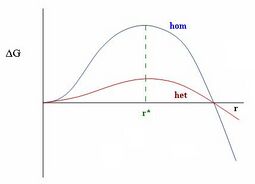
Nucleation can be divided into homogeneous nucleation and heterogeneous nucleation. First comes homogeneous nucleation, because this is much simpler. Classical nucleation theory assumes that for a microscopic nucleus of a new phase, the free energy of a droplet can be written as the sum of a bulk term, proportional to a volume and surface term.
[math]\displaystyle{ {\displaystyle \Delta G={\frac {4}{3}}\pi r^{3}\Delta g+4\pi r^{2}\sigma } }[/math]
The first term is the volume term, and, assuming that the nucleus is spherical, this is the volume of a sphere of radius [math]\displaystyle{ {\displaystyle r} }[/math]. [math]\displaystyle{ {\displaystyle \Delta g} }[/math] is the difference in free energy per unit volume between the thermodynamic phase nucleation is occurring in, and the phase that is nucleating.
critical nucleus radius, at some intermediate value of [math]\displaystyle{ {\displaystyle r} }[/math], the free energy goes through a maximum, and so the probability of formation of a nucleus goes through a minimum. There is a least-probable nucleus occurs, i.e., the one with the highest value of [math]\displaystyle{ {\displaystyle \Delta G} }[/math] where
[math]\displaystyle{ {\displaystyle {\frac {dG}{dr}}=0} }[/math]
This is called the critical nucleus and occurs at a critical nucleus radius
[math]\displaystyle{ {\displaystyle r^{*}=-{\frac {2\sigma }{\Delta g}}} }[/math]
Addition of new molecules to nuclei larger than this critical radius decreases the free energy, so these nuclei are more probable.
Heterogeneous nucleation, nucleation with the nucleus at a surface, is much more common than homogeneous nucleation. Heterogeneous nucleation is typically much faster than homogeneous nucleation because the nucleation barrier [math]\displaystyle{ {\displaystyle \Delta G^{*}} }[/math] is much lower at a surface. This is because the nucleation barrier comes from the positive term in the free energy [math]\displaystyle{ {\displaystyle \Delta G} }[/math], which is the surface term. Thus, in conclusion, the nucleation probability is highest at a surface instead of the centre of a liquid.
The Laplace pressure is the pressure difference between the inside and the outside of a curved surface between a gas region and a liquid region. The Laplace pressure is determined from the Young–Laplace equation given as
[math]\displaystyle{ \Delta P \equiv P_\text{inside} - P_\text{outside} = \gamma\left(\frac{1}{R_1}+\frac{1}{R_2}\right) }[/math].
where [math]\displaystyle{ {\displaystyle R_{1}} }[/math] and [math]\displaystyle{ {\displaystyle R_{2}} }[/math] are the principal radii of curvature and [math]\displaystyle{ {\displaystyle \gamma } }[/math] (also denoted as [math]\displaystyle{ {\displaystyle \sigma } }[/math]) is the surface tension.
The surface tension can be defined in terms of force or energy. The surface tension of a liquid is the ratio of the change in the energy of the liquid, and the change in the surface area of the liquid (that led to the change in energy). It can be defined as [math]\displaystyle{ \gamma=\frac{W}{\Delta A} }[/math]. This work W is interpreted as the potential energy.
References
- ↑ "What is Flash Freezing? (with pictures)". http://www.wisegeek.org/what-is-flash-freezing.htm.
- ↑ 2.0 2.1 2.2 "Better understanding of water's freezing behavior at nanoscale". https://www.sciencedaily.com/releases/2013/05/130521152429.htm.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 3.7 "Supercool: Water doesn't have to freeze until -48 C (-55 F)". https://www.sciencedaily.com/releases/2011/11/111123133123.htm.
- ↑ 4.0 4.1 4.2 "Superradiant matter: A new paradigm to explore dynamic phase transitions". https://www.sciencedaily.com/releases/2015/03/150318101355.htm.
- ↑ Da-Wen Sun (2001), Advances in food refrigeration, Yen-Con Hung, Cryogenic Refrigeration, p.318, Leatherhead Food Research Association Publishing, http://www.worldcat.org/title/advances-in-food-refrigeration/oclc/48154735
- ↑ "Freezing Tissue". Biotech.ufl.edu. http://www.biotech.ufl.edu/EM/data/freeze.html.
- ↑ "Preparing Competent E. coli with RF1/RF2 solutions". Personal.psu.edu. http://www.personal.psu.edu/dsg11/labmanual/DNA_manipulations/Comp_bact_by_RF1_RF2.htm.
- ↑ "Quick-Frozen Food Exactly Like Fresh." Popular Science Monthly, September 1930, pp. 26-27.
- ↑ "Freezing of fruits and vegetables". http://www.fao.org/3/y5979e/y5979e03.htm.
- ↑ 10.0 10.1 10.2 10.3 10.4 "Freezing water droplets form sharp ice peaks". https://www.sciencedaily.com/releases/2012/10/121005092911.htm.
- ↑ 11.0 11.1 "How water droplets freeze: The physics of ice and snow". https://www.sciencedaily.com/releases/2016/06/160621115439.htm.
- ↑ Duft, D (2004). Laboratory evidence for volume-dominated nucleation of ice in supercooled water microdroplets. Atmospheric Chemistry and Physics.
- ↑ Pruppacher. Klett, H.R., J.D. (1997). Microphysics of Clouds and Precipitation. Kluwer.
- ↑ Sear, R.P. (2007). Nucleation: theory and applications to protein solutions and colloidal suspensions. Physics Cond. Matt..
 |