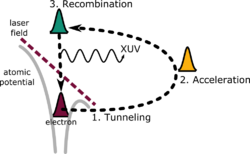Physics:High harmonic generation

Short description: Laser science process

High harmonic generation in an Argon gas jet

High-harmonic generation (HHG) is a non-linear process during which a target (gas, plasma, solid or liquid sample) is illuminated by an intense laser pulse. Under such conditions, the sample will emit the high harmonics of the generation beam (above the fifth harmonic). Due to the coherent nature of the process, high-harmonics generation is a prerequisite of attosecond physics.

Perturbative harmonic generation

Perturbative harmonic generation is a process whereby laser light of frequency ω and photon energy ħω can be used to generate new frequencies of light. The newly generated frequencies are integer multiples nω of the original light's frequency. This process was first discovered in 1961 by Franken et al., using a ruby laser, with crystalline quartz as the nonlinear medium.

Harmonic generation in dielectric solids is well understood and extensively used in modern laser physics (see second-harmonic generation). In 1967 New et al. observed the first third harmonic generation in a gas. In monatomic gases it is only possible to produce odd numbered harmonics for reasons of symmetry. Harmonic generation in the perturbative (weak field) regime is characterised by rapidly decreasing efficiency with increasing harmonic order. This behaviour can be understood by considering an atom absorbing n photons then emitting a single high energy photon. The probability of absorbing n photons decreases as n increases, explaining the rapid decrease in the initial harmonic intensities.

Development

Spectrum of a neon HHG source driven by a Ti-sapphire laser

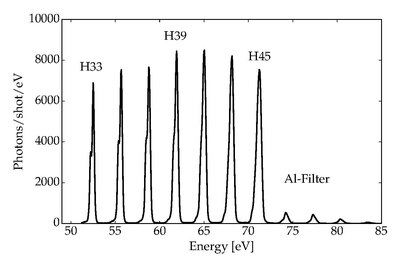
The first high harmonic generation was observed in 1977 in interaction of intense CO₂ laser pulses with plasma generated from solid targets. HHG in gases, far more widespread in application today, was first observed by McPherson and colleagues in 1987, and later by Ferray et al. in 1988, with surprising results: the high harmonics were found to decrease in intensity at low orders, as expected, but then were observed to form a plateau, with the intensity of the harmonics remaining approximately constant over many orders. Plateau harmonics spanning hundreds of eV have been measured which extend into the soft X-ray regime. This plateau ends abruptly at a position called the high harmonic cut-off.

Properties

High harmonics have a number of interesting properties. They are a tunable table-top source of XUV/soft X-rays, synchronised with the driving laser and produced with the same repetition rate. The harmonic cut-off varies linearly with increasing laser intensity up until the saturation intensity I_sat where harmonic generation stops. The saturation intensity can be increased by changing the atomic species to lighter noble gases but these have a lower conversion efficiency so there is a balance to be found depending on the photon energies required.

High harmonic generation strongly depends on the driving laser field and as a result the harmonics have similar temporal and spatial coherence properties. High harmonics are often generated with pulse durations shorter than that of the driving laser. This is due to the nonlinearity of the generation process, phase matching and ionization. Often harmonics are only produced in a very small temporal window when the phase matching condition is met. Depletion of the generating media due to ionization also means that harmonic generation is mainly confined to the leading edge of the driving pulse.

High harmonics are emitted co-linearly with the driving laser and can have a very tight angular confinement, sometimes with less divergence than that of the fundamental field and near Gaussian beam profiles.

Semi-classical approach

The maximum photon energy producible with high harmonic generation is given by the cut-off of the harmonic plateau. This can be calculated classically by examining the maximum energy the ionized electron can gain in the electric field of the laser. The cut-off energy is given by:

[math]\displaystyle{ E_{max}=I_p+3.17U_p }[/math]

where U_p is the ponderomotive energy from the laser field and I_p is the ionization potential.

This derivation of the cut-off energy is derived from a semi-classical calculation. The electron is initially treated quantum mechanically as it tunnel ionizes from the parent atom, but then its subsequent dynamics are treated classically. The electron is assumed to be born into the vacuum with zero initial velocity, and to be subsequently accelerated by the laser beam's electric field.

The three-step model

Half an optical cycle after ionization, the electron will reverse direction as the electric field changes, and will accelerate back towards the parent nucleus. Upon returning to the parent nucleus it can then emit bremsstrahlung-like radiation during a recombination process with the atom as it returns to its ground state. This description has become known as the recollisional model of high harmonic generation.

Electron return energy (full blue curve) and excursion time (blue dashed curve), as a function of the return time

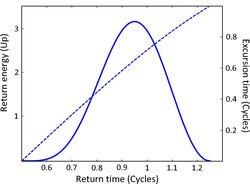
Since the frequency of the emitted radiation depends on both the kinetic energy and on the ionization potential, the different frequencies are emitted at different recombination time (i.e. the emitted pulse is chirped). What is more, for every frequency, there are two corresponding recombination times. We refer to these two trajectories as the short trajectory (which are emitted first), and the long trajectory.

Some interesting limits on the HHG process which are explained by this model show that HHG will only occur if the driving laser field is linearly polarised. Ellipticity on the laser beam causes the returning electron to miss the parent nucleus. Quantum mechanically, the overlap of the returning electron wavepacket with the nuclear wavepacket is reduced. This has been observed experimentally, where the intensity of harmonics decreases rapidly with increasing ellipticity. Another effect which limits the intensity of the driving laser is the Lorentz force. At intensities above 10¹⁶ Wcm⁻² the magnetic component of the laser pulse, which is ignored in weak field optics, can become strong enough to deflect the returning electron. This will cause it to "miss" the parent nucleus and hence prevent HHG.

Phase matching

As in every nonlinear process, phase matching plays an important role in high harmonic generation in gas phase. In free-focusing geometry, the four causes of wave vector mismatch are: neutral dispersion, plasma dispersion, Gouy phase, and dipole phase.

The neutral dispersion is caused by the atoms while the plasma dispersion is due to the ions, and the two have opposite signs. The Gouy phase is due to wavefront phase jump close to the focus, and varies along it. Finally the dipole phase arises from the atomic response in the HHG process. When using a gas jet geometry, the optimal conditions for generating high harmonics emitted from short trajectories are obtained when the generating gas is located after the focus, while generation of high harmonics from long trajectory can be obtained off-axis when the generating gas is located before the focus.

Furthermore, the implementation of loose focusing geometry for the driving field enables a higher number of emitters and photons to contribute to the generation process and thus, enhance the harmonic yield. When using a gas jet geometry, focusing the laser into the Mach disk can increase the efficiency of harmonic generation.

More generally, in the X-ray spectral region, materials have a refractive index that is very close to 1. To balance the phase mismatch, [math]\displaystyle{ \Delta k = k_q - qk_L }[/math], we need to find such parameters in the high dimensional space that will effectively make the combined refractive index at the driving laser wavelength nearly 1.

In order to achieve intensity levels that can distort an atom's binding potential, it is necessary to focus the driving laser beam. This introduces dispersion terms affecting the phase mismatch, depending on the specific geometry (such as plane wave propagation, free focusing, hollow core waveguide, etc.). Additionally, during the high harmonic generation process, electrons are accelerated, and some of them return to their parent ion, resulting in X-ray bursts. However, the majority of these electrons do not return and instead contribute to dispersion for the co-propagating waves. The returning electrons carry phase due to processes like ionization, recombination, and propagation. Furthermore, the ionized atoms can influence the refractive index of the medium, providing another source of dispersion.

The phase mismatch (>0 phase velocity of the laser is faster than that of the X-rays) can be represented as:

[math]\displaystyle{ \Delta k = k_q-qk_L = \underbrace{\Delta k_{neutrals}}_{\lt 0} + \underbrace{\Delta k_{ions}}_{\lt 0} + \underbrace{\Delta k_{electrons}}_{\gt 0} + \underbrace{\Delta k_{geometry}}_{\gt 0} + \underbrace{\Delta k_{intrinsic}}_{\gt 0} + \cdots }[/math]

where [math]\displaystyle{ \Delta k_{neutrals} }[/math] is the neutral atoms contribution, [math]\displaystyle{ \Delta k_{ions} }[/math] is the contribution from ions (when neutrals are ionized, this term can be still sufficiently large in the UV), [math]\displaystyle{ \Delta k_{electrons} }[/math] is the plasma contribution, [math]\displaystyle{ \Delta k_{geometry} }[/math] is the free focusing geometry, plane-wave of waveguiding geometry, [math]\displaystyle{ \Delta k_{intrinsic} }[/math] is the phase accumulated by the electron during the time it spends away from the atom, etc. Each term has a specific sign which allows balancing the mismatch at a particular time and frequency.

The contribution from the electrons scales quadratically with the wavelength: [math]\displaystyle{ \Delta n_{electrons} \sim -\lambda^2 }[/math], while the contribution from atoms scales inversely with wavelength: [math]\displaystyle{ \Delta n_{atoms} \sim 1/\lambda^2 }[/math]. Thus at long IR wavelengths, the term [math]\displaystyle{ \left|\Delta n_{electrons}\right| }[/math] is quite large per electron, while the term [math]\displaystyle{ \Delta n_{atoms} }[/math] is quite small and close to one. To phase-match the process of HHG, very high pressures and low ionization levels are required, thus giving a large number of emitters. In the opposite UV spectral range, the term [math]\displaystyle{ \Delta n_{atoms} }[/math] is large because of the closely located UV resonances, and in addition, the term [math]\displaystyle{ \left|\Delta n_{electrons}\right| }[/math] is small. To phase-match the process, low pressures are needed. Moreover, in the UV, very high ionization levels can be tolerated (much larger than 100%). This gives HHG photon energy scalability with the intensity of the driving UV laser. Plain-wave geometry or loose focusing geometry allows highly collinear phase matching and maximum flux extraction at the driving wavelengths where the [math]\displaystyle{ \vec{v} \times \vec{B} }[/math] term is small. The generation of High-order harmonics in waveguide allows propagation with characteristics close to those of plane wave propagation. Such geometries benefit, especially X-ray spectra generated by IR beams, where long interaction volumes are needed for optimal power extraction. In such geometries, spectra extending to 1.6 keV, have been generated. For UV-VIS driven high harmonics, the waveguide term is small, and the phase-matching picture resembles the plane-wave geometry. In such geometries, narrow bandwidth harmonics extending to the carbon edge (300 eV) have been generated.

See also

• Attosecond physics
• Nonlinear optics
• Photoionization
• Resonant high harmonic generation from laser ablated plasma plumes

External links

• Commercial EUV Laser Systems with Tabletop Scale High Harmonic Generation Sources by KMLabs