Physics:Gaussian network model

From HandWiki
Revision as of 05:41, 5 February 2024 by LinuxGuru (talk | contribs) (over-write)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Figure 1: Gaussian network model (GNM) representation of the nucleosome core particle (PDB id: 1KX4). The beads/nodes represent the residues (amino acids, gray; and nucleotides at their P (orange), C4‘- and C2-atoms (white). The nodes are connected by elastic springs (light-gray for protein intramolecular, yellow for DNA/RNA intramolecular, and cyan (protein-DNA intermolecular).

The Gaussian network model (GNM) is a representation of a biological macromolecule as an elastic mass-and-spring network to study, understand, and characterize the mechanical aspects of its long-time large-scale dynamics. The model has a wide range of applications from small proteins such as enzymes composed of a single domain, to large macromolecular assemblies such as a ribosome or a viral capsid. Protein domain dynamics plays key roles in a multitude of molecular recognition and cell signalling processes. Protein domains, connected by intrinsically disordered flexible linker domains, induce long-range allostery via protein domain dynamics. The resultant dynamic modes cannot be generally predicted from static structures of either the entire protein or individual domains.

The Gaussian network model is a minimalist, coarse-grained approach to study biological molecules. In the model, proteins are represented by nodes corresponding to α-carbons of the amino acid residues. Similarly, DNA and RNA structures are represented with one to three nodes for each nucleotide. The model uses the harmonic approximation to model interactions. This coarse-grained representation makes the calculations computationally inexpensive.

At the molecular level, many biological phenomena, such as catalytic activity of an enzyme, occur within the range of nano- to millisecond timescales. All atom simulation techniques, such as molecular dynamics simulations, rarely reach microsecond trajectory length, depending on the size of the system and accessible computational resources. Normal mode analysis in the context of GNM, or elastic network (EN) models in general, provides insights on the longer-scale functional dynamic behaviors of macromolecules. Here, the model captures native state functional motions of a biomolecule at the cost of atomic detail. The inference obtained from this model is complementary to atomic detail simulation techniques.

Another model for protein dynamics based on elastic mass-and-spring networks is the Anisotropic Network Model.

Gaussian network model theory

Figure 2: Schematic representation of nodes in elastic network of GNM. Every node is connected to its spatial neighbors by uniform springs. Distance vector between two nodes, i and j, is shown by an arrow and labeled Rij. Equilibrium positions of the ith and jth nodes, R0i and R0j, are shown in xyz coordinate system. R0ij is the equilibrium distance between nodes i and j. Instantaneous fluctuation vectors, ΔRi and ΔRj, and instantaneous distance vector, Rij, are shown by the dashed arrows.

The Gaussian network model was proposed by Bahar, Atilgan, Haliloglu and Erman in 1997.[1][2] The GNM is often analyzed using normal mode analysis, which offers an analytical formulation and unique solution for each structure. The GNM normal mode analysis differs from other normal mode analyses in that it is exclusively based on inter-residue contact topology, influenced by the theory of elasticity of Flory [3] and the Rouse model[4] and does not take the three-dimensional directionality of motions into account.

Representation of structure as an elastic network

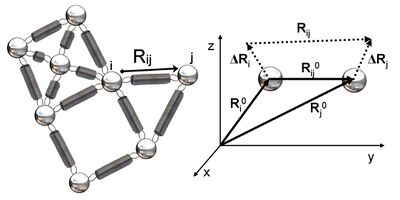
Figure 2 shows a schematic view of elastic network studied in GNM. Metal beads represent the nodes in this Gaussian network (residues of a protein) and springs represent the connections between the nodes (covalent and non-covalent interactions between residues). For nodes i and j, equilibrium position vectors, R0i and R0j, equilibrium distance vector, R0ij, instantaneous fluctuation vectors, ΔRi and ΔRj, and instantaneous distance vector, Rij, are shown in Figure 2. Instantaneous position vectors of these nodes are defined by Ri and Rj. The difference between equilibrium position vector and instantaneous position vector of residue i gives the instantaneous fluctuation vector, ΔRi = Ri - R0i. Hence, the instantaneous fluctuation vector between nodes i and j is expressed as ΔRij = ΔRj - ΔRi = Rij - R0ij.

Potential of the Gaussian network

The potential energy of the network in terms of ΔRi is

[math]\displaystyle{ V_{GNM} = \frac{\gamma}{2}\left[ \sum_{i,j}^{N} (\Delta R_j-\Delta R_i)^2 \right]= \frac{\gamma}{2}\left[ \sum_{i,j}^{N} \Delta R_i \Gamma_{ij} \Delta R_j\right] }[/math]

where γ is a force constant uniform for all springs and Γij is the ijth element of the Kirchhoff (or connectivity) matrix of inter-residue contacts, Γ, defined by

[math]\displaystyle{ \Gamma_{ij} = \left\{\begin{matrix} -1, & \mbox{if } i \ne j & \mbox{and }R_{ij} \le r_c \\ 0, & \mbox{if } i \ne j & \mbox{and }R_{ij} \gt r_c \\ -\sum_{j,j \ne i}^{N} \Gamma_{ij}, & \mbox{if } i = j \end{matrix}\right. }[/math]

rc is a cutoff distance for spatial interactions and taken to be 7 Å for amino acid pairs (represented by their α-carbons).

Expressing the X, Y and Z components of the fluctuation vectors ΔRi as ΔXT = [ΔX1 ΔX2 ..... ΔXN], ΔYT = [ΔY1 ΔY2 ..... ΔYN], and ΔZT = [ΔZ1 ΔZ2 ..... ΔZN], above equation simplifies to

[math]\displaystyle{ V_{GNM} = \frac{\gamma}{2} [\Delta X^T\Gamma \Delta X + \Delta Y^T\Gamma \Delta Y + \Delta Z^T\Gamma \Delta Z] }[/math]

Statistical mechanics foundations

In the GNM, the probability distribution of all fluctuations, P(ΔR) is isotropic

[math]\displaystyle{ P(\Delta R)=P(\Delta X,\Delta Y,\Delta Z)=p(\Delta X)p(\Delta Y)p(\Delta Z) }[/math]

and Gaussian

[math]\displaystyle{ p(\Delta X)\propto \exp\left\{ -\frac{\gamma}{2 k_B T} \Delta X^T\Gamma \Delta X \right\}=\exp\left\{ -\frac{1}{2} \left(\Delta X^T\left( \frac{k_B T}{\gamma} \Gamma^{-1} \right)^{-1} \Delta X \right) \right\} }[/math]

where kB is the Boltzmann constant and T is the absolute temperature. p(ΔY) and p(ΔZ) are expressed similarly. N-dimensional Gaussian probability density function with random variable vector x, mean vector μ and covariance matrix Σ is

[math]\displaystyle{ W(x,\mu ,\Sigma ) = \frac{1}{\sqrt{(2\pi)^N |\Sigma|}} \exp\left\{ -\frac{1}{2} (x - \mu)^T \Sigma^{-1} (x - \mu) \right\} }[/math]

[math]\displaystyle{ \sqrt{(2\pi)^N |\Sigma|} }[/math] normalizes the distribution and |Σ| is the determinant of the covariance matrix.

Similar to Gaussian distribution, normalized distribution for ΔXT = [ΔX1 ΔX2 ..... ΔXN] around the equilibrium positions can be expressed as

[math]\displaystyle{ p(\Delta X ) = \frac{1}{\sqrt{(2\pi)^N \frac{k_B T}{\gamma} |\Gamma^{-1}|}} \exp\left\{ -\frac{1}{2} \left(\Delta X^T\left( \frac{k_B T}{\gamma} \Gamma^{-1} \right)^{-1} \Delta X \right) \right\} }[/math]

The normalization constant, also the partition function ZX, is given by

[math]\displaystyle{ Z_X = \int_0^\infty \exp\left\{ -\frac{1}{2} \left(\Delta X^T\left( \frac{k_B T}{\gamma} \Gamma^{-1} \right)^{-1} \Delta X \right) \right\}d\Delta X }[/math]

where [math]\displaystyle{ \frac{k_B T}{\gamma} \Gamma^{-1} }[/math] is the covariance matrix in this case. ZY and ZZ are expressed similarly. This formulation requires inversion of the Kirchhoff matrix. In the GNM, the determinant of the Kirchhoff matrix is zero, hence calculation of its inverse requires eigenvalue decomposition. Γ−1 is constructed using the N-1 non-zero eigenvalues and associated eigenvectors. Expressions for p(ΔY) and p(ΔZ) are similar to that of p(ΔX). The probability distribution of all fluctuations in GNM becomes

[math]\displaystyle{ P(\Delta R) = p(\Delta X) p(\Delta Y) p(\Delta Z)=\frac{1}{{Z_X}{Z_Y}{Z_Z}} \exp\left\{ -\frac{3}{2} \left(\Delta X^T\left( \frac{k_B T}{\gamma} \Gamma^{-1} \right)^{-1} \Delta X \right) \right\} }[/math]

For this mass and spring system, the normalization constant in the preceding expression is the overall GNM partition function, ZGNM,

[math]\displaystyle{ Z_{GNM} = {Z_X}{Z_Y}{Z_Z} = {(2\pi)^{3N/2} \Biggl|{\frac{k_{B}T}{\gamma}{\Gamma^{-1}}}\Biggr|}^{3/2} }[/math]

Expectation values of fluctuations and correlations

The expectation values of residue fluctuations, <ΔRi2> (also called mean-square fluctuations, MSFs), and their cross-correlations, <ΔRi · ΔRj> can be organized as the diagonal and off-diagonal terms, respectively, of a covariance matrix. Based on statistical mechanics, the covariance matrix for ΔX is given by

[math]\displaystyle{ \lt \Delta X \cdot \Delta X^T \gt = \int \Delta X \cdot \Delta X^T p(\Delta X)d\Delta X=\frac{k_B T}{\gamma}\Gamma^{-1} }[/math]

The last equality is obtained by inserting the above p(ΔX) and taking the (generalized Gaussian) integral. Since,

[math]\displaystyle{ \lt \Delta X \cdot \Delta X^T \gt = \lt \Delta Y \cdot \Delta Y^T \gt = \lt \Delta Z \cdot \Delta Z^T \gt =\frac{1}{3} \lt \Delta R \cdot \Delta R^T \gt }[/math]

<ΔRi2> and <ΔRi · ΔRj> follows

[math]\displaystyle{ \lt \Delta R_i^2 \gt = \frac{3 k_B T}{\gamma}(\Gamma^{-1})_{ii} }[/math]
[math]\displaystyle{ \lt \Delta R_i \cdot \Delta R_j \gt = \frac{3 k_B T}{\gamma}(\Gamma^{-1})_{ij} }[/math]

Mode decomposition

The GNM normal modes are found by diagonalization of the Kirchhoff matrix, Γ = UΛUT. Here, U is a unitary matrix, UT = U−1, of the eigenvectors ui of Γ and Λ is the diagonal matrix of eigenvalues λi. The frequency and shape of a mode is represented by its eigenvalue and eigenvector, respectively. Since the Kirchhoff matrix is positive semi-definite, the first eigenvalue, λ1, is zero and the corresponding eigenvector have all its elements equal to 1/√N. This shows that the network model translationally invariant.

Cross-correlations between residue fluctuations can be written as a sum over the N-1 nonzero modes as

[math]\displaystyle{ \lt \Delta R_i \cdot \Delta R_j\gt = \frac{3 k_B T}{\gamma}[U\Lambda^{-1}U^T]_{ij}=\frac{3 k_B T}{\gamma}\sum_{k=1}^{N-1}\lambda_k^{-1} [u_k u_k^T]_{ij} }[/math]

It follows that, [ΔRi · ΔRj], the contribution of an individual mode is expressed as

[math]\displaystyle{ [\Delta R_i \cdot \Delta R_j]_k = \frac{3 k_B T}{\gamma}\lambda_k^{-1} [u_k]_i [u_k]_j }[/math]

where [uk]i is the ith element of uk.

Influence of local packing density

By definition, a diagonal element of the Kirchhoff matrix, Γii, is equal to the degree of a node in GNM that represents the corresponding residue’s coordination number. This number is a measure of the local packing density around a given residue. The influence of local packing density can be assessed by series expansion of Γ−1 matrix. Γ can be written as a sum of two matrices, Γ = D + O, containing diagonal elements and off-diagonal elements of Γ.

Γ−1 = (D + O)−1 = [ D (I + D−1O) ]−1 = (I + D−1O)−1D−1 = (I - D−1O + ...)−1D−1 = D−1 - D−1O D−1 + ...

This expression shows that local packing density makes a significant contribution to expected fluctuations of residues.[5] The terms that follow inverse of the diagonal matrix, are contributions of positional correlations to expected fluctuations.

GNM applications

Figure 3: Example of theoretical prediction of expected residue fluctuations for the catalytic domain of the protein Cdc25B, a cell division cycle dual-specificity phosphatase. A. Comparison of β-factors from X-ray structure (yellow) and theoretical calculations (red). B. Structure of catalytic domain of Cdc25B colored according to theoretical motility of regions. Light blue regions, e.g. topmost alpha-helix next to the catalytic site of this protein, are expected to be more mobile than the rest of the domain. C. Cross-correlation map i.e. normalized <ΔRi·ΔRj> values. Red-colored regions correspond to collective residue motions and blue-colored regions correspond to uncorrelated motions. The results are retrieved iGNM server. PDB ID of Cdc25B is 1QB0.

Equilibrium fluctuations

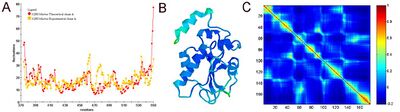
Equilibrium fluctuations of biological molecules can be experimentally measured. In X-ray crystallography the B-factor (also called Debye-Waller or temperature factor) of each atom is a measure of its mean-square fluctuation near its equilibrium position in the native structure. In NMR experiments, this measure can be obtained by calculating root-mean-square differences between different models. In many applications and publications, including the original articles, it has been shown that expected residue fluctuations obtained by the GNM are in good agreement with the experimentally measured native state fluctuations.[6][7] The relation between B-factors, for example, and expected residue fluctuations obtained from GNM is as follows

[math]\displaystyle{ B_i = \frac{8\pi^2}{3}\lt \Delta R_{i} \cdot \Delta R_{i} \gt = \frac{8\pi^2 k_B T}{\gamma}(\Gamma^{-1})_{ii} }[/math]

Figure 3 shows an example of GNM calculation for the catalytic domain of the protein Cdc25B, a cell division cycle dual-specificity phosphatase.

Figure 4: Slow modes obtained from GNM calculations are depicted on Cdc2B catalytic domain. A. Plot of the slowest mode. B. Mapping of the amplitude of motion in the slowest mode onto protein structure. The alpha-helix nearby the catalytic site of this domain is the most mobile region of the protein along the slowest mode. Expected values of fluctuations were also highest at this region, as shown in Figure 3. The results are retrieved iGNM server. PDB ID of Cdc25B is 1QB0.

Physical meanings of slow and fast modes

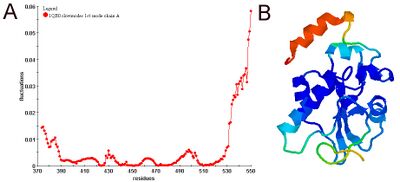
Diagonalization of the Kirchhoff matrix decomposes the conformational motions into a spectrum of collective modes. The expected values of fluctuations and cross-correlations are obtained from linear combinations of fluctuations along these normal modes. The contribution of each mode is scaled with the inverse of that modes frequency. Hence, slow (low frequency) modes contribute most to the expected fluctuations. Along the few slowest modes, motions are shown to be collective and global and potentially relevant to functionality of the biomolecules. Fast (high frequency) modes, on the other hand, describe uncorrelated motions not inducing notable changes in the structure. GNM-based methods do not provide real dynamics but only an approximation based on the combination and interpolation of normal modes.[8] Their applicability strongly depends on how collective the motion is.[8][9]

Other specific applications

There are several major areas in which the Gaussian network model and other elastic network models have proved to be useful.[10] These include:

  • Spring bead based network model: In spring-bead based network model, the springs and beads are used as components in the crosslinked network. Springs are cross-linked to represent mechanical behavior of the material and bridge molecular dynamics (MD) model and finite element (FE) model (see Figure. 5). The beads represent material mass of cluster bonds. Each spring is used to represent a cluster of polymer chains, instead of part of a single polymer chain. This simplification allows to bridge different models at multiple length scales and improves the simulation efficiency significantly. At each iteration step in the simulation, forces in the springs are applied to the nodes at the center of the beads, and the equilibrated nodal displacements throughout the system are calculated. Different from the traditional FE method for obtaining stress and strain, the spring–bead model provides the displacements of the nodes and forces in the springs. The equivalent strain and strain energy of spring–bead based network model can be defined and calculated using the displacements of nodes and the spring characteristics. Furthermore, the results from the network model can be scaled up to obtain the structural response at the macroscale using FE analysis.[11][12]
  • Decomposition of flexible/rigid regions and domains of proteins [13][14][15]
  • Characterization of functional motions and functionally important sites/residues of proteins, enzymes and large macromolecular assemblies [16][11][17][18][19][20][21][22][23][24][25][26]
  • Refinement and dynamics of low-resolution structural data, e.g. Cryo-electron microscopy[27][28][29][30]
  • Molecular replacement for solving X-ray structures, when a conformational change occurred, with respect to a known structure[31]
  • Integration with atomistic models and simulations [32][33]
  • Investigation of folding/unfolding pathways and kinetics.[34][35]
  • Annotation of functional implication in molecular evolution [36][37]

Web servers

In practice, two kinds of calculations can be performed. The first kind (the GNM per se) makes use of the Kirchhoff matrix.[1][2] The second kind (more specifically called either the Elastic Network Model or the Anisotropic Network Model) makes use of the Hessian matrix associated to the corresponding set of harmonic springs.[38] Both kinds of models can be used online, using the following servers.

GNM servers

ENM/ANM servers

Other relevant servers

See also

References

Primary sources

  • Bahar, I.; Atilgan, A. R.; Erman, B. (1997). "Direct evaluation of thermal fluctuations in protein using a single parameter harmonic potential". Folding & Design 2 (3): 173–181. doi:10.1016/s1359-0278(97)00024-2. PMID 9218955. 
  • Haliloglu, T. Bahar; Erman, B. (1997). "Gaussian dynamics of folded proteins". Phys. Rev. Lett. 79 (16): 3090–3093. doi:10.1103/physrevlett.79.3090. Bibcode: 1997PhRvL..79.3090H. 
  • Cui Q, Bahar I, (2006). Normal Mode Analysis: Theory and applications to biological and chemical systems, Chapman & Hall/CRC, London, UK

Specific citations

  1. ↑ 1.0 1.1 Bahar, I.; Atilgan, A. R.; Erman, B. (1997). "Direct evaluation of thermal fluctuations in protein using a single parameter harmonic potential". Folding & Design 2 (3): 173–181. doi:10.1016/s1359-0278(97)00024-2. PMID 9218955. 
  2. ↑ 2.0 2.1 Haliloglu, T. Bahar; Erman, B (1997). "Gaussian dynamics of folded proteins". Phys. Rev. Lett. 79 (16): 3090–3093. doi:10.1103/physrevlett.79.3090. Bibcode: 1997PhRvL..79.3090H. 
  3. ↑ Flory, P.J. (1976). "Statistical thermodynamics of random networks". Proc. R. Soc. Lond. A 351 (1666): 351. doi:10.1098/rspa.1976.0146. Bibcode: 1976RSPSA.351..351F. 
  4. ↑ Rouse, P.E. (1953). "A Theory of the Linear Viscoelastic Properties of Dilute Solutions of Coiling Polymers". J. Chem. Phys. 21 (7): 1272. doi:10.1063/1.1699180. Bibcode: 1953JChPh..21.1272R. 
  5. ↑ Halle, B (2002). "Flexibility and packing in proteins". Proc. Natl. Acad. Sci. U.S.A. 99 (3): 1274–1279. doi:10.1073/pnas.032522499. PMID 11818549. Bibcode: 2002PNAS...99.1274H. 
  6. ↑ Bahar, I.; Wallqvist, A.; Covell, D. G.; Jernigan, R.L. (1998). "Correlation between native state hydrogen exchange and cooperative residue fluctuations from a simple model". Biochemistry 37 (4): 1067–1075. doi:10.1021/bi9720641. PMID 9454598. 
  7. ↑ Bahar, I.; Atilgan, A. R.; Demirel, M. C.; Erman, B. (1998). "Vibrational dynamics of proteins: Significance of slow and fast modes in relation to function and stability". Phys. Rev. Lett. 80 (12): 2733–2736. doi:10.1103/physrevlett.80.2733. Bibcode: 1998PhRvL..80.2733B. 
  8. ↑ 8.0 8.1 Kmiecik, Sebastian; Kouza, Maksim; Badaczewska-Dawid, Aleksandra E.; Kloczkowski, Andrzej; Kolinski, Andrzej (2018). "Modeling of Protein Structural Flexibility and Large-Scale Dynamics: Coarse-Grained Simulations and Elastic Network Models" (in en). International Journal of Molecular Sciences 19 (11): 3496. doi:10.3390/ijms19113496. PMID 30404229. 
  9. ↑ Yang, Lei; Song, Guang; Jernigan, Robert L. (2007-08-01). "How well can we understand large-scale protein motions using normal modes of elastic network models?". Biophysical Journal 93 (3): 920–929. doi:10.1529/biophysj.106.095927. ISSN 0006-3495. PMID 17483178. Bibcode: 2007BpJ....93..920Y. 
  10. ↑ Chennubhotla, C; Rader, AJ; Yang, LW; Bahar, I (2005). "Elastic network models for understanding biomolecular machinery: from enzymes to supramolecular assemblies". Phys. Biol. 2 (4): S173–S180. doi:10.1088/1478-3975/2/4/S12. PMID 16280623. Bibcode: 2005PhBio...2S.173C. 
  11. ↑ 11.0 11.1 Zhang, Jinjun (2015). "An optimized cross-linked network model to simulate the linear elastic material response of a smart polymer". Journal of Intelligent Material Systems and Structures 27 (11): 1461–1475. doi:10.1177/1045389X15595292. https://www.researchgate.net/publication/282062448. 
  12. ↑ Zhang, Jinjun (2015). "A novel statistical spring-bead based network model for self-sensing smart polymer materials". Smart Materials and Structures 24 (8): 085022. doi:10.1088/0964-1726/24/8/085022. Bibcode: 2015SMaS...24h5022Z. https://www.researchgate.net/publication/280222102. 
  13. ↑ Hinsen, K (1999). "Analysis of domain motions by approximate normal mode calculations". Proteins 33 (3): 417–429. doi:10.1002/(sici)1097-0134(19981115)33:3<417::aid-prot10>3.0.co;2-8. PMID 9829700. 
  14. ↑ Rader, AJ.; Anderson, G.; Isin, B.; Khorana, H. G.; Bahar, I.; Klein-Seetharaman, J. (2004). "Identification of core amino acids stabilizing rhodopsin". Proc. Natl. Acad. Sci. U.S.A. 101 (19): 7246–7251. doi:10.1073/pnas.0401429101. PMID 15123809. Bibcode: 2004PNAS..101.7246R. 
  15. ↑ Kundu, S.; Sorensen, D.C.; Phillips, G.N. Jr (2004). "Automatic domain decomposition of proteins by a Gaussian Network Model". Proteins 57 (4): 725–733. doi:10.1002/prot.20268. PMID 15478120. 
  16. ↑ Zhang, Jinjun (2015). "A novel statistical spring-bead based network model for self-sensing smart polymer materials". Smart Materials and Structures 24 (8): 085022. doi:10.1088/0964-1726/24/8/085022. Bibcode: 2015SMaS...24h5022Z. https://www.researchgate.net/publication/280222102. 
  17. ↑ Keskin, O. (2002). "Relating molecular flexibility to function: a case study of tubulin". Biophys. J. 83 (2): 663–80. doi:10.1016/s0006-3495(02)75199-0. PMID 12124255. Bibcode: 2002BpJ....83..663K. 
  18. ↑ Temiz NA & Bahar I, Inhibitor binding alters the directions of domain motions in HIV-1 reverse transcriptase, Proteins: Structure, Function and Genetics 49, 61-70, 2002.
  19. ↑ Xu, C., Tobi, D. and Bahar, I. 2003 Allosteric changes in protein structure computed by a simple mechanical model: hemoglobin T<-> R2 transition, J. Mol. Biol., 333, 153.
  20. ↑ Dror Tobi & Ivet Bahar, Structural Changes Involved in Protein Binding Correlate with intrinsic Motions of Proteins in the Unbound State, Proc Natl Acad Sci (USA) 102, 18908-18913, 2005.
  21. ↑ Shrivastava, Indira H.; Bahar, Ivet (2006). "Common Mechanism of Pore Opening Shared by Five Different Potassium Channels". Biophys J 90 (11): 3929–3940. doi:10.1529/biophysj.105.080093. PMID 16533848. Bibcode: 2006BpJ....90.3929S. 
  22. ↑ Yang, LW; Bahar, I (2005). "Coupling between Catalytic Site and Collective Dynamics: A requirement for Mechanochemical Activity of Enzymes". Structure 13 (6): 893–904. doi:10.1016/j.str.2005.03.015. PMID 15939021. 
  23. ↑ Chennubhotla, Chakra; Bahar, Ivet (2006). "Markov Methods for Hierarchical Coarse-Graining of Large Protein Dynamics". Research in Computational Molecular Biology. Lecture Notes in Computer Science. 3909. pp. 379–393. doi:10.1007/11732990_32. ISBN 978-3-540-33295-4. https://archive.org/details/lccn_2006922626/page/379. 
  24. ↑ Wang, Y. Rader; AJ; Bahar, I.; Jernigan, RL. (2004). "Global Ribosome Motions Revealed with Elastic Network Model". J. Struct. Biol. 147 (3): 302–314. doi:10.1016/j.jsb.2004.01.005. PMID 15450299. 
  25. ↑ Rader, AJ; Vlad, Daniel; Bahar, Ivet (2005). "Maturation Dynamics of Bacteriophage HK97 Capsid". Structure 13 (3): 413–21. doi:10.1016/j.str.2004.12.015. PMID 15766543. 
  26. ↑ Hamacher, K.; Trylska, J.; McCammon, J.A. (2006). "Dependency Map of Proteins in the Small Ribosomal Subunit". PLOS Comput. Biol. 2 (2): e10. doi:10.1371/journal.pcbi.0020010. PMID 16485038. Bibcode: 2006PLSCB...2...10H. 
  27. ↑ Ming, D. (2002). "How to describe protein motion without amino acid sequence and atomic coordinates". Proc. Natl. Acad. Sci. U.S.A. 99 (13): 8620–8625. doi:10.1073/pnas.082148899. PMID 12084922. Bibcode: 2002PNAS...99.8620M. 
  28. ↑ Tama, F.; Wriggers, W.; Brooks III, C.L. (2002). "Exploring global distortions of biological macromolecules and assemblies from low-resolution structural information and elastic network theory". J. Mol. Biol. 321 (2): 297–305. doi:10.1016/s0022-2836(02)00627-7. PMID 12144786. 
  29. ↑ Delarue, M.; Dumas, P. (2004). "On the use of low-frequency normal modes to enforce collective movements in refining macromolecular structural models". Proc. Natl. Acad. Sci. U.S.A. 101 (18): 6957–6962. doi:10.1073/pnas.0400301101. PMID 15096585. Bibcode: 2004PNAS..101.6957D. 
  30. ↑ Micheletti, C.; Carloni, P.; Maritan, A. (2004). ""Accurate and efficient description of protein vibrational dynamics " comparing molecular dynamics and gaussian models". Proteins 55 (3): 635–45. doi:10.1002/prot.20049. PMID 15103627. Bibcode: 2004cond.mat..5145M. 
  31. ↑ Suhre, K.; Sanejouand, Y.H. (2004). "On the potential of normal mode analysis for solving difficult molecular replacement problems". Acta Crystallogr. D 60 (4): 796–9. doi:10.1107/s0907444904001982. PMID 15039589. 
  32. ↑ Zhang, Z.Y.; Shi, Y.Y.; Liu, H.Y. (2003). "Molecular dynamics simulations of peptides and proteins with amplified collective motions". Biophys. J. 84 (6): 3583–93. doi:10.1016/s0006-3495(03)75090-5. PMID 12770868. Bibcode: 2003BpJ....84.3583Z. 
  33. ↑ Micheletti, C.; Lattanzi, G.; Maritan, A. (2002). "Elastic properties of proteins: insight on the folding process and evolutionary selection of native structures". J. Mol. Biol. 321 (5): 909–21. doi:10.1016/s0022-2836(02)00710-6. PMID 12206770. Bibcode: 2002cond.mat..4400M. 
  34. ↑ Micheletti, C. (2002). "Crucial stages of protein folding through a solvable model: predicting target sites for enzyme-inhibiting drugs". Protein Science 11 (8): 1878–87. doi:10.1110/ps.3360102. PMID 12142442. Bibcode: 2002cond.mat..9325M. 
  35. ↑ Portman, J.J.; Takada, S.; Wolynes, P.G. (2001). "Microscopic theory of protein folding rates. I. fine structure of the free energy profile and folding routes from a variational approach". J. Chem. Phys. 114 (11): 5069. doi:10.1063/1.1334662. Bibcode: 2001JChPh.114.5069P. 
  36. ↑ Hamacher, K (2008). "Relating Sequence Evolution of HIV1-Protease to Its Underlying Molecular Mechanics". Gene 422 (1–2): 30–36. doi:10.1016/j.gene.2008.06.007. PMID 18590806. 
  37. ↑ Hamacher, K.; McCammon, J.A. (2006). "Computing the amino acid specificity of fluctuations in biomolecular systems". J. Chem. Theory Comput. 2 (3): 873–8. doi:10.1021/ct050247s. PMID 26626694. 
  38. ↑ Tirion, M.M. (1996). "Large amplitude elastic motions in proteins from a single-parameter, atomic analysis". Phys. Rev. Lett. 77 (9): 1905–1908. doi:10.1103/physrevlett.77.1905. PMID 10063201. Bibcode: 1996PhRvL..77.1905T. 
  39. ↑ Li, H., Chang, Y. Y., Yang, L. W., & Bahar, I. (2016). iGNM 2.0: the Gaussian network model database for biomolecular structural dynamics. Nucleic Acids Research, 44(D1), D415-D422.
  40. ↑ Atilgan, AR; Durrell, SR; Jernigan, RL; Demirel, MC; Keskin, O.; Bahar, I. (2001). "Anisotropy of fluctuation dynamics of proteins with an elastic network model". Biophys. J. 80 (1): 505–515. doi:10.1016/s0006-3495(01)76033-x. PMID 11159421. Bibcode: 2001BpJ....80..505A. 
  41. ↑ Bakan, A.; Meireles, L. M.; Bahar, I. (2011). "ProDy: protein dynamics inferred from theory and experiments". Bioinformatics 27 (11): 1575–1577. doi:10.1093/bioinformatics/btr168. PMID 21471012. 
  42. ↑ Bakan, A.; Dutta, A.; Mao, W.; Liu, Y.; Chennubhotla, C.; Lezon, T. R.; Bahar, I. (2014). "Evol and ProDy for bridging protein sequence evolution and structural dynamics". Bioinformatics 30 (18): 2681–2683. doi:10.1093/bioinformatics/btu336. PMID 24849577. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Gaussian_network_model&oldid=3284234"