Hook length formula

Short description: Mathematical formula for the number of Young tableaux

In combinatorial mathematics, the hook length formula is a formula for the number of standard Young tableaux whose shape is a given Young diagram. It has applications in diverse areas such as representation theory, probability, and algorithm analysis; for example, the problem of longest increasing subsequences. A related formula gives the number of semi-standard Young tableaux, which is a specialization of a Schur polynomial.

Definitions and statement

Let [math]\displaystyle{ \lambda=(\lambda_1\geq \cdots\geq \lambda_k) }[/math] be a partition of [math]\displaystyle{ n=\lambda_1+\cdots+\lambda_k }[/math]. It is customary to interpret [math]\displaystyle{ \lambda }[/math] graphically as a Young diagram, namely a left-justified array of square cells with [math]\displaystyle{ k }[/math] rows of lengths [math]\displaystyle{ \lambda_1,\ldots,\lambda_k }[/math]. A (standard) Young tableau of shape [math]\displaystyle{ \lambda }[/math] is a filling of the [math]\displaystyle{ n }[/math] cells of the Young diagram with all the integers [math]\displaystyle{ \{1,\ldots,n\} }[/math], with no repetition, such that each row and each column form increasing sequences. For the cell in position [math]\displaystyle{ (i,j) }[/math], in the [math]\displaystyle{ i }[/math]th row and [math]\displaystyle{ j }[/math]th column, the hook [math]\displaystyle{ H_\lambda(i,j) }[/math] is the set of cells [math]\displaystyle{ (a,b) }[/math] such that [math]\displaystyle{ a=i }[/math] and [math]\displaystyle{ b \ge j }[/math] or [math]\displaystyle{ a \ge i }[/math] and [math]\displaystyle{ b=j }[/math]. The hook length [math]\displaystyle{ h_\lambda(i,j) }[/math] is the number of cells in [math]\displaystyle{ H_\lambda(i,j) }[/math].

The hook length formula expresses the number of standard Young tableaux of shape [math]\displaystyle{ \lambda }[/math], denoted by [math]\displaystyle{ f^{\lambda} }[/math] or [math]\displaystyle{ d_\lambda }[/math], as

[math]\displaystyle{ f^\lambda = \frac{n!}{\prod h_\lambda (i,j)} , }[/math]

where the product is over all cells [math]\displaystyle{ (i,j) }[/math] of the Young diagram.

Examples

A tableau listing the hook length of each cell in the Young diagram
[math]\displaystyle{ (4, 3, 1, 1) }[/math]

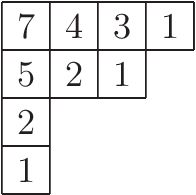
The figure on the right shows hook lengths for the cells in the Young diagram [math]\displaystyle{ \lambda=(4,3,1,1) }[/math], corresponding to the partition 9 = 4 + 3 + 1 + 1. The hook length formula gives the number of standard Young tableaux as:

[math]\displaystyle{ f^\lambda = \frac{9!}{7\cdot 5\cdot 4\cdot 3\cdot 2\cdot 2\cdot 1\cdot 1\cdot 1} = 216. }[/math]

A Catalan number [math]\displaystyle{ C_n }[/math]counts Dyck paths with [math]\displaystyle{ n }[/math] steps going up (U) interspersed with [math]\displaystyle{ n }[/math] steps going down (D), such that at each step there are never more preceding D's than U's. These are in bijection with the Young tableaux of shape [math]\displaystyle{ \lambda=(n,n) }[/math]: a Dyck path corresponds to the tableau whose first row lists the positions of the U-steps, while the second row lists the positions of the D-steps. For example, UUDDUD correspond to the tableaux with rows 125 and 346.

This shows that [math]\displaystyle{ C_n = f^{(n,n)} }[/math], so the hook formula specializes to the well-known product formula

[math]\displaystyle{ C_n = \frac{(2n)!}{(n+1)(n)\cdots(3)(2)(n)(n-1)\cdots(2)(1)} = \frac{(2n)!}{(n+1)!\,n!} = \frac{1}{n{+}1}\binom{2n}{n}. }[/math]

History

There are other formulas for [math]\displaystyle{ f^\lambda }[/math], but the hook length formula is particularly simple and elegant. A less convenient formula expressing [math]\displaystyle{ f^\lambda }[/math] in terms of a determinant was deduced independently by Frobenius and Young in 1900 and 1902 respectively using algebraic methods. MacMahon found an alternate proof for the Young–Frobenius formula in 1916 using difference methods.

The hook length formula itself was discovered in 1953 by Frame, Robinson, and Thrall as an improvement to the Young–Frobenius formula. Sagan describes the discovery as follows.

One Thursday in May of 1953, Robinson was visiting Frame at Michigan State University. Discussing the work of Staal (a student of Robinson), Frame was led to conjecture the hook formula. At first Robinson could not believe that such a simple formula existed, but after trying some examples he became convinced, and together they proved the identity. On Saturday they went to the University of Michigan, where Frame presented their new result after a lecture by Robinson. This surprised Thrall, who was in the audience, because he had just proved the same result on the same day!

Despite the simplicity of the hook length formula, the Frame–Robinson–Thrall proof is not very insightful and does not provide any intuition for the role of the hooks. The search for a short, intuitive explanation befitting such a simple result gave rise to many alternate proofs. Hillman and Grassl gave the first proof that illuminates the role of hooks in 1976 by proving a special case of the Stanley hook-content formula, which is known to imply the hook length formula. Greene, Nijenhuis, and Wilf found a probabilistic proof using the hook walk in which the hook lengths appear naturally in 1979. Remmel adapted the original Frame–Robinson–Thrall proof into the first bijective proof for the hook length formula in 1982. A direct bijective proof was first discovered by Franzblau and Zeilberger in 1982. Zeilberger also converted the Greene–Nijenhuis–Wilf hook walk proof into a bijective proof in 1984. A simpler direct bijection was announced by Pak and Stoyanovskii in 1992, and its complete proof was presented by the pair and Novelli in 1997.

Meanwhile, the hook length formula has been generalized in several ways. R. M. Thrall found the analogue to the hook length formula for shifted Young Tableaux in 1952. Sagan gave a shifted hook walk proof for the hook length formula for shifted Young tableaux in 1980. Sagan and Yeh proved the hook length formula for binary trees using the hook walk in 1989. Proctor gave a poset generalization (see below).

Probabilistic proof

Knuth's heuristic argument

The hook length formula can be understood intuitively using the following heuristic, but incorrect, argument suggested by D. E. Knuth. Given that each element of a tableau is the smallest in its hook and filling the tableau shape at random, the probability that cell [math]\displaystyle{ (i,j) }[/math] will contain the minimum element of the corresponding hook is the reciprocal of the hook length. Multiplying these probabilities over all [math]\displaystyle{ i }[/math] and [math]\displaystyle{ j }[/math] gives the formula. This argument is fallacious since the events are not independent.

Knuth's argument is however correct for the enumeration of labellings on trees satisfying monotonicity properties analogous to those of a Young tableau. In this case, the 'hook' events in question are in fact independent events.

Probabilistic proof using the hook walk

This is a probabilistic proof found by C. Greene, A. Nijenhuis, and H. S. Wilf in 1979. Define

[math]\displaystyle{ e_\lambda = \frac{n!}{\prod_{(i,j)\in Y(\lambda)}h_\lambda(i,j)}. }[/math]

We wish to show that [math]\displaystyle{ f^\lambda = e_\lambda }[/math]. First,

[math]\displaystyle{ f^\lambda = \sum_{\mu\uparrow\lambda}f^\mu, }[/math]

Corners of the Young diagram (5,3,2,1,1)

where the sum runs over all Young diagrams [math]\displaystyle{ \mu }[/math] obtained from [math]\displaystyle{ \lambda }[/math] by deleting one corner cell. (The maximal entry of the Young tableau of shape [math]\displaystyle{ \lambda }[/math] occurs at one of its corner cells, so deleting it gives a Young tableaux of shape [math]\displaystyle{ \mu }[/math].)

We define [math]\displaystyle{ f^\emptyset=1 }[/math]and [math]\displaystyle{ e_{\emptyset}=1 }[/math], so it is enough to show the same recurrence

[math]\displaystyle{ e_\lambda = \sum_{\mu\uparrow\lambda}e_\mu, }[/math]

which would imply [math]\displaystyle{ f^\lambda=e_\lambda }[/math] by induction. The above sum can be viewed as a sum of probabilities by writing it as

[math]\displaystyle{ \sum_{\mu\uparrow\lambda}\frac{e_\mu}{e_\lambda}=1. }[/math]

We therefore need to show that the numbers [math]\displaystyle{ \frac{e_\mu}{e_\lambda} }[/math] define a probability measure on the set of Young diagrams [math]\displaystyle{ \mu }[/math] with [math]\displaystyle{ \mu\uparrow\lambda }[/math]. This is done in a constructive way by defining a random walk, called the hook walk, on the cells of the Young diagram [math]\displaystyle{ \lambda }[/math], which eventually selects one of the corner cells of [math]\displaystyle{ \lambda }[/math] (which are in bijection with diagrams [math]\displaystyle{ \mu }[/math] for which [math]\displaystyle{ \mu\uparrow\lambda }[/math]). The hook walk is defined by the following rules.

1. Pick a cell uniformly at random from [math]\displaystyle{ |\lambda| }[/math] cells. Start the random walk from there.
2. Successor of current cell [math]\displaystyle{ (i,j) }[/math] is chosen uniformly at random from the hook [math]\displaystyle{ H_{\lambda}(i,j)\setminus \{(i,j)\} }[/math].
3. Continue until you reach a corner cell [math]\displaystyle{ \textbf{c} }[/math].

Proposition: For a given corner cell [math]\displaystyle{ (a,b) }[/math] of [math]\displaystyle{ \lambda }[/math], we have

[math]\displaystyle{ \mathbb{P}\left(\textbf{c}=(a,b)\right)=\frac{e_\mu}{e_\lambda}, }[/math]

where [math]\displaystyle{ \mu=\lambda\setminus\{(a,b)\} }[/math].

Given this, summing over all corner cells [math]\displaystyle{ (a,b) }[/math] gives [math]\displaystyle{ \sum_{\mu\uparrow\lambda}\frac{e_{\mu}}{e_{\lambda}}=1 }[/math] as claimed.

Connection to representations of the symmetric group

The hook length formula is of great importance in the representation theory of the symmetric group [math]\displaystyle{ S_n }[/math], where the number [math]\displaystyle{ f^\lambda }[/math] is known to be equal to the dimension of the complex irreducible representation [math]\displaystyle{ V_\lambda }[/math] associated to [math]\displaystyle{ \lambda }[/math].

Detailed discussion

The complex irreducible representations [math]\displaystyle{ V_{\lambda} }[/math] of the symmetric group are indexed by partitions [math]\displaystyle{ \lambda }[/math] of [math]\displaystyle{ n }[/math] (see Specht module) . Their characters are related to the theory of symmetric functions via the Hall inner product:

[math]\displaystyle{ \chi^\lambda(w)=\langle s_\lambda, p_{\tau(w)}\rangle, }[/math]

where [math]\displaystyle{ s_{\lambda} }[/math] is the Schur function associated to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ p_{\tau(w)} }[/math] is the power-sum symmetric function of the partition [math]\displaystyle{ \tau(w) }[/math] associated to the cycle decomposition of [math]\displaystyle{ w }[/math]. For example, if [math]\displaystyle{ w=(154)(238)(6)(79) }[/math] then [math]\displaystyle{ \tau(w) = (3,3,2,1) }[/math].

Since the identity permutation [math]\displaystyle{ e }[/math] has the form [math]\displaystyle{ e=(1)(2)\cdots(n) }[/math] in cycle notation, [math]\displaystyle{ \tau(e) = (1,\ldots,1)=1^{(n)} }[/math], the formula says

[math]\displaystyle{ f^\lambda \,=\, \dim V_\lambda \,=\,\chi^\lambda(e) \,=\, \langle s_\lambda, p_{1^{(n)}}\rangle }[/math]

The expansion of Schur functions in terms of monomial symmetric functions uses the Kostka numbers:

[math]\displaystyle{ s_\lambda= \sum_\mu K_{\lambda\mu}m_\mu, }[/math]

Then the inner product with [math]\displaystyle{ p_{1^{(n)}} = h_{1^{(n)}} }[/math] is [math]\displaystyle{ K_{\lambda 1^{(n)}} }[/math], because [math]\displaystyle{ \langle m_{\mu},h_{\nu} \rangle = \delta_{\mu\nu} }[/math]. Note that [math]\displaystyle{ K_{\lambda 1^{(n)}} }[/math] is equal to [math]\displaystyle{ f^{\lambda}=\dim V_\lambda }[/math], so that [math]\displaystyle{ \textstyle \sum_{\lambda\vdash n} \left(f^{\lambda}\right)^2 = n! }[/math] from considering the regular representation of [math]\displaystyle{ S_n }[/math], or combinatorially from the Robinson–Schensted–Knuth correspondence.

The computation also shows that:

[math]\displaystyle{ (x_1+x_2+\cdots+x_k)^n = \sum_{\lambda\vdash n} s_\lambda f^\lambda. }[/math]

This is the expansion of [math]\displaystyle{ p_{1^{(n)}} }[/math] in terms of Schur functions using the coefficients given by the inner product, since [math]\displaystyle{ \langle s_{\mu},s_{\nu}\rangle = \delta_{\mu\nu} }[/math]. The above equality can be proven also checking the coefficients of each monomial at both sides and using the Robinson–Schensted–Knuth correspondence or, more conceptually, looking at the decomposition of [math]\displaystyle{ V^{\otimes n} }[/math] by irreducible [math]\displaystyle{ GL(V) }[/math] modules, and taking characters. See Schur–Weyl duality.

Proof of hook formula using Frobenius formula

By the above considerations

[math]\displaystyle{ p_{1^{(n)}} = \sum_{\lambda\vdash n} s_{\lambda}f^{\lambda} }[/math]

so that

[math]\displaystyle{ \Delta(x)p_{1^{(n)}} = \sum_{\lambda\vdash n} \Delta(x)s_{\lambda}f^{\lambda} }[/math]

where [math]\displaystyle{ \Delta(x) = \prod_{i\lt j} (x_i-x_j) }[/math] is the Vandermonde determinant.

For the partition [math]\displaystyle{ \lambda = (\lambda_1\geq\cdots\geq\lambda_k) }[/math], define [math]\displaystyle{ l_i = \lambda_i+k-i }[/math] for [math]\displaystyle{ i=1,\ldots,k }[/math]. For the following we need at least as many variables as rows in the partition, so from now on we work with [math]\displaystyle{ n }[/math] variables [math]\displaystyle{ x_1,\cdots,x_n }[/math].

Each term [math]\displaystyle{ \Delta(x)s_{\lambda} }[/math] is equal to

[math]\displaystyle{ a_{(\lambda_1+k-1, \lambda_2+k-2, \dots , \lambda_k)} (x_1, x_2, \dots , x_k) \ =\ \det\! \left[ \begin{matrix} x_1^{l_1} & x_2^{l_1} & \dots & x_k^{l_1} \\ x_1^{l_2} & x_2^{l_2} & \dots & x_k^{l_2} \\ \vdots & \vdots & \ddots & \vdots \\ x_1^{l_k} & x_2^{l_k} & \dots & x_k^{l_k} \end{matrix} \right] }[/math]

(See Schur function.) Since the vector [math]\displaystyle{ (l_1,\ldots, l_k) }[/math] is different for each partition, this means that the coefficient of [math]\displaystyle{ x_1^{l_1}\cdots x_k^{l_k} }[/math] in [math]\displaystyle{ \Delta(x)p_{1^{(n)}} }[/math], denoted [math]\displaystyle{ \left[\Delta(x)p_{1^{(n)}}\right]_{l_1,\cdots,l_k} }[/math], is equal to [math]\displaystyle{ f^{\lambda} }[/math]. This is known as the Frobenius Character Formula, which gives one of the earliest proofs.

It remains only to simplify this coefficient. Multiplying

[math]\displaystyle{ \Delta(x) \ =\ \sum_{w\in S_n} \sgn(w) x_1^{w(1)-1}x_2^{w(2)-1}\cdots x_k^{w(k)-1} }[/math]

and

[math]\displaystyle{ p_{1^{(n)}} \ =\ (x_1+x_2+\cdots+x_k)^n \ =\ \sum \frac{n!}{d_1!d_2!\cdots d_k!} x_1^{d_1}x_2^{d_2}\cdots x_k^{d_k} }[/math]

we conclude that our coefficient as

[math]\displaystyle{ \sum_{w\in S_n} \sgn(w)\frac{n!}{(l_1-w(1)+1)!\cdots (l_k-w(k)+1)!} }[/math]

which can be written as

[math]\displaystyle{ \frac{n!}{l_1!l_2!\cdots l_k!} \sum_{w\in S_n} \sgn(w)\left[(l_1)(l_1-1)\cdots(l_1-w(1)+2)\right] \left[(l_2)(l_2-1)\cdots(l_2-w(2)+2)\right]\left[(l_k)(l_k-1)\cdots(l_k-w(k)+2)\right] }[/math]

The latter sum is equal to the following determinant

[math]\displaystyle{ \det \left[ \begin{matrix} 1 & l_1 & l_1(l_1-1) & \dots & \prod_{i=0}^{k-2} (l_1-i) \\ 1 & l_2 & l_2(l_2-1) & \dots & \prod_{i=0}^{k-2} (l_2-i)\\ \vdots & \vdots & \vdots& \ddots & \vdots \\ 1 & l_k & l_k(l_k-1) & \dots & \prod_{i=0}^{k-2} (l_k-i) \end{matrix} \right] }[/math]

which column-reduces to a Vandermonde determinant, and we obtain the formula

[math]\displaystyle{ f^\lambda = \frac{n!}{l_1!\,l_2!\cdots l_k!} \prod_{i\lt j} (l_i-l_j). }[/math]

Note that [math]\displaystyle{ l_i }[/math] is the hook length of the first box in each row of the Young diagram, and this expression is easily transformed into the desired form [math]\displaystyle{ \frac{n!}{\prod h_\lambda (i,j)} }[/math]: one shows [math]\displaystyle{ \textstyle l_i! = \prod_{j \gt i} (l_i - l_j) \cdot \prod_{j\leq\lambda_i} h_\lambda(i,j) }[/math], where the latter product runs over the [math]\displaystyle{ i }[/math]th row of the Young diagram.

Connection to longest increasing subsequences

The hook length formula also has important applications to the analysis of longest increasing subsequences in random permutations. If [math]\displaystyle{ \sigma_n }[/math] denotes a uniformly random permutation of order [math]\displaystyle{ n }[/math], [math]\displaystyle{ L(\sigma_n) }[/math] denotes the maximal length of an increasing subsequence of [math]\displaystyle{ \sigma_n }[/math], and [math]\displaystyle{ \ell_n }[/math] denotes the expected (average) value of [math]\displaystyle{ L(\sigma_n) }[/math], Anatoly Vershik and Sergei Kerov and independently Benjamin F. Logan and Lawrence A. Shepp showed that when [math]\displaystyle{ n }[/math] is large, [math]\displaystyle{ \ell_n }[/math] is approximately equal to [math]\displaystyle{ 2 \sqrt{n} }[/math]. This answers a question originally posed by Stanislaw Ulam. The proof is based on translating the question via the Robinson–Schensted correspondence to a problem about the limiting shape of a random Young tableau chosen according to Plancherel measure. Since the definition of Plancherel measure involves the quantity [math]\displaystyle{ f^\lambda }[/math], the hook length formula can then be used to perform an asymptotic analysis of the limit shape and thereby also answer the original question.

The ideas of Vershik–Kerov and Logan–Shepp were later refined by Jinho Baik, Percy Deift and Kurt Johansson, who were able to achieve a much more precise analysis of the limiting behavior of the maximal increasing subsequence length, proving an important result now known as the Baik–Deift–Johansson theorem. Their analysis again makes crucial use of the fact that [math]\displaystyle{ f^\lambda }[/math] has a number of good formulas, although instead of the hook length formula it made use of one of the determinantal expressions.

Related formulas

The formula for the number of Young tableaux of shape [math]\displaystyle{ \lambda }[/math] was originally derived from the Frobenius determinant formula in connection to representation theory:

[math]\displaystyle{ f(\lambda_1,\ldots,\lambda_k) = \frac{n! \,\Delta(\lambda_k,\lambda_{k-1}+1,\ldots,\lambda_1 + k - 1)}{\lambda_k ! \,(\lambda_{k-1} + 1)! \cdots (\lambda_1 + k - 1)!}. }[/math]

Hook lengths can also be used to give a product representation to the generating function for the number of reverse plane partitions of a given shape. If λ is a partition of some integer p, a reverse plane partition of n with shape λ is obtained by filling in the boxes in the Young diagram with non-negative integers such that the entries add to n and are non-decreasing along each row and down each column. The hook lengths [math]\displaystyle{ h_1,\dots,h_p }[/math] can be defined as with Young tableaux. If π_n denotes the number of reverse plane partitions of n with shape λ, then the generating function can be written as

[math]\displaystyle{ \sum_{n=0}^\infty \pi_n x^n = \prod_{k=1}^p (1-x^{h_k})^{-1} }[/math]

Stanley discovered another formula for the same generating function. In general, if [math]\displaystyle{ A }[/math] is any poset with [math]\displaystyle{ n }[/math] elements, the generating function for reverse [math]\displaystyle{ A }[/math]-partitions is

[math]\displaystyle{ \frac{P(x)}{(1-x)(1-x^2)\cdots(1-x^n)} }[/math]

where [math]\displaystyle{ P(x) }[/math] is a polynomial such that [math]\displaystyle{ P(1) }[/math] is the number of linear extensions of [math]\displaystyle{ A }[/math].

In the case of a partition [math]\displaystyle{ \lambda }[/math], we are considering the poset in its cells given by the relation

[math]\displaystyle{ (i,j) \leq (i',j') \iff i\leq i' \qquad \textrm{and} \qquad j\leq j' }[/math].

So a linear extension is simply a standard Young tableau, i.e. [math]\displaystyle{ P(1) = f^{\lambda} }[/math]

Proof of hook formula using Stanley's formula

Combining the two formulas for the generating functions we have

[math]\displaystyle{ \frac{P(x)}{(1-x)(1-x^2)\cdots(1-x^n)} = \prod_{(i,j)\in \lambda} (1-x^{h_{(i,j)}})^{-1} }[/math]

Both sides converge inside the disk of radius one and the following expression makes sense for [math]\displaystyle{ |x| \lt 1 }[/math]

[math]\displaystyle{ P(x) = \frac{\prod_{k=1}^n (1-x^k)}{\prod_{(i,j)\in \lambda} (1-x^{h_{(i,j)}})}. }[/math]

It would be violent to plug in 1, but the right hand side is a continuous function inside the unit disk and a polynomial is continuous everywhere so at least we can say

[math]\displaystyle{ P(1) = \lim_{x\to 1} \frac{\prod_{k=1}^n (1-x^k)}{\prod_{(i,j)\in \lambda} (1-x^{h_{(i,j)}})}. }[/math]

Applying L'Hôpital's rule [math]\displaystyle{ n }[/math] times yields the hook length formula

[math]\displaystyle{ P(1) = \frac{n!}{\prod_{(i,j)\in \lambda}h_{(i,j)}}. }[/math]

Semi-standard tableaux hook length formula

The Schur polynomial [math]\displaystyle{ s_\lambda(x_1,\ldots,x_k) }[/math] is the generating function of semistandard Young tableaux with shape [math]\displaystyle{ \lambda }[/math] and entries in [math]\displaystyle{ \{1,\ldots,k\} }[/math]. Specializing this to [math]\displaystyle{ x_i = 1 }[/math] gives the number of semi-standard tableaux, which can be written in terms of hook lengths:

[math]\displaystyle{ s_\lambda(1,\ldots,1)\ =\ \prod_{(i,j)\in \mathrm{Y}(\lambda)}\frac{k-i+j}{h_\lambda(i,j)}. }[/math]

The Young diagram [math]\displaystyle{ \lambda }[/math] corresponds to an irreducible representation of the special linear group [math]\displaystyle{ \mathrm{SL}_k(\mathbb C) }[/math], and the Schur polynomial is also the character of the diagonal matrix [math]\displaystyle{ \mathrm{diag}(x_1,\ldots,x_k) }[/math] acting on this representation. The above specialization is thus the dimension of the irreducible representation, and the formula is an alternative to the more general Weyl dimension formula.

We may refine this by taking the principal specialization of the Schur function in the variables [math]\displaystyle{ 1,t,t^2\!,t^3\!, \ldots }[/math] :

[math]\displaystyle{ s_{\lambda}(1,t,t^2,\ldots) \ =\ \frac{t^{n\left( \lambda\right)}}{\prod_{(i,j)\in Y(\lambda)}(1-t^{h_{\lambda}(i,j)})} , }[/math]

where [math]\displaystyle{ n(\lambda) = \sum_i (i{-}1)\lambda_i = \sum_i \tbinom{\lambda_i'}{2} }[/math] for the conjugate partition [math]\displaystyle{ \lambda' }[/math].

Skew shape formula

There is a generalization of this formula for skew shapes,

[math]\displaystyle{ s_{\lambda/\mu}(1,t,t^2,\cdots) = \sum_{S \in E(\lambda/\mu)} \prod_{(i,j) \in \lambda\setminus S} \frac{t^{\lambda_j'-i}}{1-t^{h(i,j)}} }[/math]

where the sum is taken over excited diagrams of shape [math]\displaystyle{ \lambda }[/math] and boxes distributed according to [math]\displaystyle{ \mu }[/math].

A variation on the same theme is given by Okounkov and Olshanski of the form

[math]\displaystyle{ \frac{\dim\lambda/\mu}{\dim\lambda}=\frac{s^*_\mu(\lambda)}{|\lambda|!/|\mu|!}, }[/math]

where [math]\displaystyle{ s^*_\mu }[/math] is the so-called shifted Schur function [math]\displaystyle{ s^*_\mu(x_1,\dots,x_n)=\frac{\det[(x_i+n-1)!/(\mu_j+n-j)!]}{\det[(x_i+n-i)!/(n-j)!]} }[/math].

Generalization to d-complete posets

Young diagrams can be considered as finite order ideals in the poset [math]\displaystyle{ \mathbb{N}\times\mathbb{N} }[/math], and standard Young tableaux are their linear extensions. Robert Proctor has given a generalization of the hook length formula to count linear extensions of a larger class of posets generalizing both trees and skew diagrams.

External links

• The Surprising Mathematics of Longest Increasing Subsequences by Dan Romik. Contains discussions of the hook length formula and several of its variants, with applications to the mathematics of longest increasing subsequences.