Triangulation (topology)
thumb|250px|Another triangulation of the torus
In mathematics, triangulation describes the replacement of topological spaces by piecewise linear spaces, i.e. the choice of a homeomorphism in a suitable simplicial complex. Spaces being homeomorphic to a simplicial complex are called triangulable. Triangulation has various uses in different branches of mathematics, for instance in algebraic topology, in complex analysis or in modeling.
Motivation
On the one hand, it is sometimes useful to forget about superfluous information of topological spaces: The replacement of the original spaces with simplicial complexes may help to recognize crucial properties and to gain a better understanding of the considered object.
On the other hand, simplicial complexes are objects of combinatorial character and therefore one can assign them quantities rising from their combinatorial pattern, for instance, the Euler characteristic. Triangulation allows now to assign such quantities to topological spaces.
Investigations concerning the existence and uniqueness of triangulations established a new branch in topology, namely the piecewise-linear-topology (short PL- topology). Its main purpose is topological properties of simplicial complexes and its generalization, cell-complexes.
Simplicial complexes
Abstract simplicial complexes
An abstract simplicial complex above a set [math]\displaystyle{ V }[/math] is a system [math]\displaystyle{ \mathcal{T} \subset \mathcal{P} (V) }[/math] of non-empty subsets such that:
- [math]\displaystyle{ \{v_0\} \in \mathcal{T} }[/math] for each [math]\displaystyle{ v_0\in V }[/math];
- if [math]\displaystyle{ E \in \mathcal{T} }[/math] and [math]\displaystyle{ \emptyset \neq F\subset E }[/math] [math]\displaystyle{ \Rightarrow }[/math] [math]\displaystyle{ F \in \mathcal{T} }[/math].
The elements of [math]\displaystyle{ \mathcal{T} }[/math] are called simplices, the elements of [math]\displaystyle{ V }[/math] are called vertices. A simplex with [math]\displaystyle{ n+1 }[/math] vertices has dimension [math]\displaystyle{ n }[/math] by definition. The dimension of an abstract simplicial complex is defined as [math]\displaystyle{ \text{dim}(\mathcal{T})= \text{sup}\;\{\text{dim}(F):F \in \mathcal{T}\} \in \mathbb{N}\cup \infty }[/math].[1]
Abstract simplicial complexes can be thought of as geometrical objects too. This requires the term of geometric simplex.
Geometric simplices
Let [math]\displaystyle{ p_0,...p_n }[/math] be [math]\displaystyle{ n+1 }[/math] affinely independent points in [math]\displaystyle{ \mathbb{R}^n }[/math], i.e. the vectors [math]\displaystyle{ (p_1-p_0), (p_2-p_0),\dots (p_n-p_0) }[/math]are linearly independent. The set [math]\displaystyle{ \Delta = \Bigl\{x \in \mathbb{R}^n \;\Big|\; x= \sum_{i=0}^n t_ip_i\; with \; 0\leq t_i\leq 1\; and \; \sum_{i=0}^n t_i =1 \Bigr\} }[/math] is said to be the simplex spanned by [math]\displaystyle{ p_0,...p_n }[/math]. It has dimension [math]\displaystyle{ n }[/math] by definition. The points [math]\displaystyle{ p_0,...p_n }[/math] are called the vertices of [math]\displaystyle{ \Delta }[/math], the simplices spanned by [math]\displaystyle{ n }[/math] of the [math]\displaystyle{ n+1 }[/math] vertices are called faces and the boundary [math]\displaystyle{ \partial \Delta }[/math] is defined to be the union of its faces.
The [math]\displaystyle{ n }[/math]-dimensional standard-simplex is the simplex spanned by the unit vectors [math]\displaystyle{ e_0,...e_n }[/math][2]
Geometric simplicial complexes
A geometric simplicial complex [math]\displaystyle{ \mathcal{S}\subset \mathbb{R}^n }[/math] is a union of geometric simplices such that
- If [math]\displaystyle{ S }[/math] is a simplex in [math]\displaystyle{ \mathcal{S} }[/math], then all its faces are in [math]\displaystyle{ \mathcal{S} }[/math].
- If [math]\displaystyle{ S, T }[/math] are two distinct simplices in [math]\displaystyle{ \mathcal{S} }[/math], their interiors are disjoint.
The set [math]\displaystyle{ \mathcal{S} }[/math] can be realized as a topological space [math]\displaystyle{ |\mathcal{S}| }[/math] by choosing the closed sets to be [math]\displaystyle{ \Bigl\{A \subset |\mathcal{S}|\; \Big| \; A\cap \Delta }[/math] is closed for all [math]\displaystyle{ \Delta \in \mathcal{S} \Bigr\} }[/math]. It should be mentioned, that in general, the simplicial complex won't provide the natural topology of [math]\displaystyle{ \mathbb{R}^n }[/math]. In the case that each point in the complex lies only in finetly many simplices, both topologies coincide[2]
Each geometric complex can be associated with an abstract complex by choosing as a ground set [math]\displaystyle{ V }[/math] the set of vertices that appear in any simplex of [math]\displaystyle{ \mathcal{S} }[/math] and as system of subsets the subsets of [math]\displaystyle{ V }[/math] which correspond to vertex sets of simplices in [math]\displaystyle{ \mathcal{S} }[/math].
A natural question is if vice versa, any abstract simplicial complex corresponds to a geometric complex. In general, the geometric construction as mentioned here is not flexible enough: Consider for instance abstract simplicial complex of infinite dimension. However, the following more abstract construction provides a topological space for any kind of abstract simplicial complex:
Let [math]\displaystyle{ \mathcal{T} }[/math] be an abstract simplicial complex above a set [math]\displaystyle{ V }[/math]. Choose a union of simplices [math]\displaystyle{ (\Delta_F)_{F \in \mathcal{T}} }[/math], but each in [math]\displaystyle{ \mathbb {R}^N }[/math] of dimension sufficiently large, such that the geometric simplex [math]\displaystyle{ \Delta_F }[/math] is of dimension [math]\displaystyle{ n }[/math] if the abstract geometric simplex [math]\displaystyle{ F }[/math] has dimension [math]\displaystyle{ n }[/math]. If [math]\displaystyle{ E\subset F }[/math], [math]\displaystyle{ \Delta_E\subset \mathbb{R}^N }[/math]can be identified with a face of [math]\displaystyle{ \Delta_F\subset\mathbb{R}^M }[/math] and the resulting topological space is the gluing [math]\displaystyle{ \Delta_E \cup_{i}\Delta_F }[/math] Effectuating the gluing for each inclusion, one ends up with the desired topological space.
As in the previous construction, by the topology induced by gluing, the closed sets in this space are the subsets being closed in the subspace topology of each simplex [math]\displaystyle{ \Delta_F }[/math].
The simplicial complex [math]\displaystyle{ \mathcal{T_n} }[/math], which consists of all simplices [math]\displaystyle{ \mathcal{T} }[/math] of dimension [math]\displaystyle{ \leq n }[/math] is called the [math]\displaystyle{ n }[/math]-th skeleton of [math]\displaystyle{ \mathcal{T} }[/math].
A natural neighborhood of a vertex [math]\displaystyle{ V }[/math] of a simplicial complex [math]\displaystyle{ \mathcal{S} }[/math] is considered to be the star [math]\displaystyle{ star(K)= \Big \{ L \in \mathcal{S} \; |\; K \subset L \Big\} }[/math] of a simplex, its boundary is the link
[math]\displaystyle{ lk(K)= \Big\{ M \in \mathcal{S} \; | \; M \cap K = \empty \Big\} }[/math].
Simplicial maps
The maps considered in this category are simplicial maps: Let [math]\displaystyle{ \mathcal{K} }[/math], [math]\displaystyle{ \mathcal{L} }[/math] be abstract simplicial complexes above sets [math]\displaystyle{ V_K }[/math], [math]\displaystyle{ V_L }[/math]. A simplicial map is a function [math]\displaystyle{ f:V_K \rightarrow V_L }[/math] which maps each simplex in [math]\displaystyle{ \mathcal{K} }[/math] onto a simplex in [math]\displaystyle{ \mathcal{L} }[/math]. By affine-linear extension on the simplices, [math]\displaystyle{ f }[/math] induces a map between the geometric realizations of the complexes.[2]
Examples
- Let [math]\displaystyle{ W =\{a,b,c,d,e,f\} }[/math] and let [math]\displaystyle{ \mathcal{T} = \Big\{ \{a\}, \{b\},\{c\},\{d\},\{e\},\{f\}, \{a,b\},\{a,c\},\{a,d\},\{a,e\},\{a,f\}\Big\} }[/math]. The associated geometric complex is a star with center [math]\displaystyle{ \{a\} }[/math].
- Let [math]\displaystyle{ V= \{A,B,C,D\} }[/math] and let [math]\displaystyle{ \mathcal{S} = \mathcal{P}(V) }[/math]. Its geometric realization [math]\displaystyle{ |\mathcal{S}| }[/math] is a tetrahedron.
- Let [math]\displaystyle{ V }[/math] as above and let [math]\displaystyle{ \mathcal{S}' =\; \mathcal{P}(\mathcal{V})\setminus \{A,B,C,D\} }[/math]. The geometric simplicial complex is the boundary of a tetrahedron [math]\displaystyle{ |\mathcal{S'}| = \partial |\mathcal{S}| }[/math].
Definition
A triangulation of a topological space [math]\displaystyle{ X }[/math] is a homeomorphism [math]\displaystyle{ t: |\mathcal{T}|\rightarrow X }[/math] where [math]\displaystyle{ \mathcal{T} }[/math] is a simplicial complex. Topological spaces do not necessarily admit a triangulation and if they do, it is not necessarily unique.
Examples
- Simplicial complexes can be triangulated by identity.
- Let [math]\displaystyle{ \mathcal{S}, \mathcal{S'} }[/math] be as in the examples seen above. The closed unit ball [math]\displaystyle{ \mathbb{D}^3 }[/math] is homeomorphic to a tetrahedron so it admits a triangulation, namely the homeomorphism [math]\displaystyle{ t:|\mathcal{S}| \rightarrow \mathbb{D}^3 }[/math]. Restricting [math]\displaystyle{ t }[/math] to [math]\displaystyle{ |\mathcal{S}'| }[/math] yields a homeomorphism [math]\displaystyle{ t':|\mathcal{S}'| \rightarrow \mathbb{S}^2 }[/math].
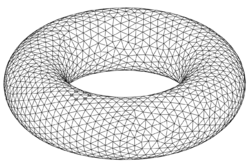
- The torus [math]\displaystyle{ \mathbb{T}^2 = \mathbb{S}^1 \times \mathbb{S}^1 }[/math] admits a triangulation. To see this, consider the torus as a square where the parallel faces are glued together. This square can be triangulated as shown below:
- The projective plane [math]\displaystyle{ \mathbb{P}^2 }[/math] admits a triangulation (see CW-complexes)
- One can show that differentiable manifolds admit triangulations.[3]
Invariants
Triangulations of spaces allow assigning combinatorial invariants rising from their dedicated simplicial complexes to spaces. These are characteristics that equal for complexes that are isomorphic via a simplicial map and thus have the same combinatorial pattern.
This data might be useful to classify topological spaces up to homeomorphism but only given that the characteristics are also topological invariants, meaning, they do not depend on the chosen triangulation. For the data listed here, this is the case.[4] For details and the link to singular homology, see topological invariance
Homology
Via triangulation, one can assign a chain complex to topological spaces that arise from its simplicial complex and compute its simplicial homology. Compact spaces always admit finite triangulations and therefore their homology groups are finitely generated and only finitely many of them do not vanish. Other data as Betti- Numbers or Euler characteristic can be derived from homology.
Betti- numbers and Euler-characteristics
Let [math]\displaystyle{ |\mathcal{S}| }[/math] be a finite simplicial complex. The [math]\displaystyle{ n }[/math]- th Betti- number [math]\displaystyle{ b_n(\mathcal{S}) }[/math] is defined to be the rank of the [math]\displaystyle{ n }[/math]- th simplicial homology- group of the spaces. These numbers encode geometric properties of the spaces: The Betti- Number [math]\displaystyle{ b_0(\mathcal{S}) }[/math] for instance represents the number of connected components. For a triangulated, closed orientable surfaces [math]\displaystyle{ F }[/math], [math]\displaystyle{ b_1(F)= 2g }[/math] holds where [math]\displaystyle{ g }[/math] denotes the genus of the surface: Therefore its first Betti- number represents the doubled number of handles of the surface.[5]
With the comments above, for compact spaces all Betti- numbers are finite and almost all are zero. Therefore, one can form their alternating sum
[math]\displaystyle{ \sum_{k=0}^{\infty} (-1)^{k}b_k(\mathcal{L}) }[/math]
which is called the Euler Charakteristik of the complex, a catchy topological invariant.
Topological invariance
To use these invariants for the classification of topological spaces up to homeomorphism one needs invariance of the characteristics regarding homeomorphism.
A famous approach to the question was at the beginning of the 20th century the attempt to show that any two triangulations of the same topological space admit a common subdivision. This assumption is known as Hauptvermutung ( German: Main assumption). Let [math]\displaystyle{ |\mathcal{L}|\subset \mathbb{R}^N }[/math] be a simplicial complex. A complex [math]\displaystyle{ |\mathcal{L'}|\subset \mathbb{R}^N }[/math] is said to be a subdivision of [math]\displaystyle{ \mathcal{L} }[/math] iff:
- every simplex of [math]\displaystyle{ \mathcal{L'} }[/math] is contained in a simplex of [math]\displaystyle{ \mathcal{L} }[/math] and
- every simplex of [math]\displaystyle{ \mathcal{L} }[/math] is a finite union of simplices in [math]\displaystyle{ \mathcal{L'} }[/math] .[2]
Those conditions ensure that subdivisions does not change the simplicial complex as a set or as a topological space. A map [math]\displaystyle{ f: \mathcal{K} \rightarrow \mathcal{L} }[/math] between simplicial complexes is said to be piecewise linear if there is a refinement [math]\displaystyle{ \mathcal{K'} }[/math] of [math]\displaystyle{ \mathcal{K} }[/math] such that [math]\displaystyle{ f }[/math] is piecewise linear on each simplex of [math]\displaystyle{ \mathcal{K} }[/math]. Two complexes that correspond to another via piecewise linear bijection are said to be combinatorial isomorphic. In particular, two complexes that have a common refinement are combinatorially equivalent. Homology groups are invariant to combinatorial equivalence and therefore the Hauptvermutung would give the topological invariance of simplicial homology groups. In 1918, Alexander introduced the concept of singular homology. Henceforth, most of the invariants arising from triangulation were replaced by invariants arising from singular homology. For those new invariants, it can be shown that they were invariant regarding homeomorphism and even regarding homotopy equivalence.[6] Furthermore it was shown that singular and simplicial homology groups coincide.[6] This workaround has shown the invariance of the data to homeomorphism. Hauptvermutung lost in importance but it was initial for a new branch in topology: The piecewise linear (short PL- topology) topology examines topological properties of topological spaces.[7]
Hauptvermutung
The Hauptvermutung (German for main conjecture) states that two triangulations always admit a common subdivision. Originally, its purpose was to prove invariance of combinatorial invariants regarding homeomorphisms. The assumption that such subdivisions exist in general is intuitive, as subdivision are easy to construct for simple spaces, for instance for low dimensional manifolds. Indeed the assumption was proven for manifolds of dimension [math]\displaystyle{ \leq 3 }[/math] and for differentiable manifolds but it was disproved in general:[8] An important tool to show that triangulations do not admit a common subdivision. i. e their underlying complexes are not combinatorially isomorphic is the combinatorial invariant of Reidemeister Torsion.
Reidemeister-Torsion
To disprove the Hauptvermutung it is helpful to use combinatorial invariants which are not topological invariants. A famous example is Reidemeister-Torsion. It can be assigned to a tuple [math]\displaystyle{ (K,L) }[/math] of CW- complexes: If [math]\displaystyle{ L = \emptyset }[/math] this characteristic will be a topological invariant but if [math]\displaystyle{ L \neq \emptyset }[/math] in general not. An approach to Hauptvermutung was to find homeomorphic spaces with different values of Reidemeister-Torsion. This invariant was used initially to classify lens- spaces and first counterexamples to the Hauptvermutung were built based on lens- spaces:[8]
Classification of lens- spaces
In its original formulation, Lens spaces are 3-manifolds, constructed as quotient spaces of the 3-sphere: Let [math]\displaystyle{ p, q }[/math] be natural numbers, such that [math]\displaystyle{ p, q }[/math] are coprime . The lens space [math]\displaystyle{ L(p,q) }[/math] is defined to be the orbit space of the free group action
[math]\displaystyle{ \Z/p\Z\times S^{3}\to S^{3} }[/math]
[math]\displaystyle{ (k,(z_1,z_2)) \mapsto (z_1 \cdot e^{2\pi i k/p}, z_2 \cdot e^{2\pi i kq/p} ) }[/math].
For different tuples [math]\displaystyle{ (p, q) }[/math], Lens spaces will be homotopy- equivalent but not homeomorphic. Therefore they can't be distinguished with the help of classical invariants as the fundamental group but by the use of Reidemeister-Torsion.
Two Lens spaces [math]\displaystyle{ L(p,q_1), L(p,q_2) }[/math]are homeomorphic, if and only if [math]\displaystyle{ q_1 \equiv \pm q_2^{\pm 1} \pmod{p} }[/math].[9] This is the case iff two Lens spaces are simple-homotopy-equivalent. The fact can be used to construct counterexamples for the Hauptvermutung as follows. Suppose there are spaces [math]\displaystyle{ L'_1, L'_2 }[/math] derived from non-homeomorphic Lens spaces [math]\displaystyle{ L(p,q_1), L(p,q_2) }[/math]having different Reidemeister torsion. Suppose further that the modification into [math]\displaystyle{ L'_1, L'_2 }[/math] does not affect Reidemeister torsion but such that after modification [math]\displaystyle{ L'_1 }[/math] and [math]\displaystyle{ L'_2 }[/math] are homeomorphic. The resulting spaces will disprove the Hauptvermutung.
Existence of triangulation
Besides the question of concrete triangulations for computational issues, there are statements about spaces that are easier to prove given that they are simplicial complexes. Especially manifolds are of interest. Topological manifolds of dimension [math]\displaystyle{ \leq 3 }[/math] are always triangulable[10][11][1] but there are non-triangulable manifolds for dimension [math]\displaystyle{ n }[/math], for [math]\displaystyle{ n }[/math] arbitrary but greater than three.[12][13] Further, differentiable manifolds always admit triangulations.[3]
PL- Structures
Manifolds are an important class of spaces. It is natural to require them not only to be triangulable but moreover to admit a piecewise linear atlas, a PL- structure:
Let [math]\displaystyle{ |X| }[/math] be a simplicial complex such that every point admits an open neighborhood [math]\displaystyle{ U }[/math] such that there is a triangulation of [math]\displaystyle{ U }[/math] and a piecewise linear homeomorphism [math]\displaystyle{ f: U \rightarrow \mathbb{R}^n }[/math]. Then [math]\displaystyle{ |X| }[/math] is said to be a piecewise linear (PL) manifold of dimension [math]\displaystyle{ n }[/math] and the triangulation together with the PL- atlas is said to be a PL- structure on [math]\displaystyle{ |X| }[/math].
An important lemma is the following:
Let [math]\displaystyle{ X }[/math] be a topological space. It is equivalent
- [math]\displaystyle{ X }[/math] is an [math]\displaystyle{ n }[/math]-dimensional manifold and admits a PL- structure.
- There is a triangulation of [math]\displaystyle{ X }[/math] such that the link of each vertex is an [math]\displaystyle{ n-1 }[/math] sphere.
- For each triangulation of [math]\displaystyle{ X }[/math] the link of each vertex is an [math]\displaystyle{ n-1 }[/math] sphere.
The equivalence of the second and the third statement is because that the link of a vertex is independent of the chosen triangulation up to combinatorial isomorphism.[14] One can show that differentiable manifolds admit a PL- structure as well as manifolds of dimension [math]\displaystyle{ \leq 3 }[/math].[15] Counterexamples for the triangulation conjecture are counterexamples for the conjecture of the existence of PL- structure of course.
Moreover, there are examples for triangulated spaces which do not admit a PL- structure. Consider an [math]\displaystyle{ n-2 }[/math]- dimensional PL- Homology-sphere [math]\displaystyle{ X }[/math]. The double suspension [math]\displaystyle{ S^2X }[/math] is a topological [math]\displaystyle{ n }[/math]-sphere. Choosing a triangulation [math]\displaystyle{ t: |\mathcal{S}| \rightarrow S^2 X }[/math] obtained via the suspension operation on triangulations the resulting simplicial complex is not a PL- manifold, because there is a vertex [math]\displaystyle{ v }[/math] such that [math]\displaystyle{ link(v) }[/math] is not a [math]\displaystyle{ n-1 }[/math] sphere.[16]
A question arising with the definition is if PL-structures are always unique: Given two PL- structures for the same space [math]\displaystyle{ Y }[/math], is there a there a homeomorphism [math]\displaystyle{ F:Y\rightarrow Y }[/math] which is piecewise linear with respect to both PL- structures? The assumption is similar to the Hauptvermutung and indeed there are spaces which have different PL-structures which are not equivalent. Triangulation of PL- equivalent spaces can be transformed into one another via Pachner moves:
Pachner Moves
Pachner moves are a way to manipulate triangulations: Let [math]\displaystyle{ \mathcal{S} }[/math] be a simplicial complex. For two simplices [math]\displaystyle{ K, L }[/math] the Join
[math]\displaystyle{ K*L= \Big\{ tk+(1-t)l\;|\;k\in K,l\in L \;t \in [0,1]\Big\} }[/math] are the points lying on straights between points in [math]\displaystyle{ K }[/math] and in [math]\displaystyle{ L }[/math]. Choose [math]\displaystyle{ S \in \mathcal{S} }[/math] such that [math]\displaystyle{ lk(S)= \partial K }[/math] for any [math]\displaystyle{ K }[/math] lying not in [math]\displaystyle{ \mathcal{S} }[/math]. A new complex [math]\displaystyle{ \mathcal{S'} }[/math], can be obtained by replacing [math]\displaystyle{ S * \partial K }[/math] by [math]\displaystyle{ \partial S * K }[/math]. This replacement is called a Pachner move. The theorem of Pachner states that whenever two triangulated manifolds are PL- equivalent, there is a series of Pachner moves transforming both into another.[17]
CW-complexes

A similar but more flexible construction than simplicial complexes is the one of CW-complexes. Its construction is as follows:
An [math]\displaystyle{ n }[/math]- cell is the closed [math]\displaystyle{ n }[/math]- dimensional unit-ball [math]\displaystyle{ B_n= [0,1]^n }[/math], an open [math]\displaystyle{ n }[/math]-cell is its inner [math]\displaystyle{ B_n= [0,1]^n\setminus \mathbb{S}^{n-1} }[/math]. Let [math]\displaystyle{ X }[/math] be a topological space, let [math]\displaystyle{ f: \mathbb{S}^{n-1}\rightarrow X }[/math] be a continuous map. The gluing [math]\displaystyle{ X \cup_{f}B_n }[/math] is said to be obtained by gluing on an [math]\displaystyle{ n }[/math]-cell.
A cell complex is a union [math]\displaystyle{ X=\cup_{n\geq 0} X_n }[/math] of topological spaces such that
- [math]\displaystyle{ X_0 }[/math] is a discrete set
- each [math]\displaystyle{ X_n }[/math] is obtained from [math]\displaystyle{ X_{n-1} }[/math] by gluing on a family of [math]\displaystyle{ n }[/math]-cells.
Each simplicial complex is a CW-complex, the inverse is not true. The construction of CW- complexes can be used to define cellular homology and one can show that cellular homology and simplicial homology coincide.[18] For computational issues, it is sometimes easier to assume spaces to be CW- complexes and determine their homology via cellular decomposition, an example is the projective plane [math]\displaystyle{ \mathbb{P}^2 }[/math]: Its construction as a CW-complex needs three cells, whereas its simplicial complex consists of 54 simplices.
Other Applications
Classification of manifolds
By triangulating 1-dimensional manifolds, one can show that they are always homeomorphic to disjoint copies of the real line and the unit sphere [math]\displaystyle{ \mathbb{S}^1 }[/math]. Moreover, surfaces, i.e. 2-manifolds, can be classified completely: Let [math]\displaystyle{ S }[/math] be a compact surface.
- If [math]\displaystyle{ S }[/math] is orientable, it is homeomorphic to a 2-sphere with [math]\displaystyle{ n }[/math] tori of dimension [math]\displaystyle{ 2 }[/math] attached, for some [math]\displaystyle{ n\geq 0 }[/math].
- If [math]\displaystyle{ S }[/math] is not orientable, it is homeomorphic to a Klein Bottle with [math]\displaystyle{ n }[/math] tori of dimension [math]\displaystyle{ 2 }[/math] attached, for some [math]\displaystyle{ n\geq 0 }[/math].
To prove this theorem one constructs a fundamental polygon of the surface: This can be done by using the simplicial structure obtained by the triangulation.[19]
Maps on simplicial complexes
Giving spaces the structure of a simplicial structure might help to understand maps defined on the spaces. The maps can often be assumed to be simplicial maps via the simplicial approximation theorem:
Simplicial approximation
Let [math]\displaystyle{ \mathcal{K} }[/math], [math]\displaystyle{ \mathcal{L} }[/math] be abstract simplicial complexes above sets [math]\displaystyle{ V_K }[/math], [math]\displaystyle{ V_L }[/math]. A simplicial map is a function [math]\displaystyle{ f:V_K \rightarrow V_L }[/math] which maps each simplex in [math]\displaystyle{ \mathcal{K} }[/math] onto a simplex in [math]\displaystyle{ \mathcal{L} }[/math]. By affin-linear extension on the simplices, [math]\displaystyle{ f }[/math] induces a map between the geometric realizations of the complexes. Each point in a geometric complex lies in the inner of exactly one simplex, its support. Consider now a continuous map [math]\displaystyle{ f:\mathcal{K}\rightarrow \mathcal{L} }[/math]. A simplicial map [math]\displaystyle{ g:\mathcal{K}\rightarrow \mathcal{L} }[/math] is said to be a simplicial approximation of [math]\displaystyle{ f }[/math] if and only if each [math]\displaystyle{ x \in \mathcal{K} }[/math] is mapped by [math]\displaystyle{ g }[/math] onto the support of [math]\displaystyle{ f(x) }[/math] in [math]\displaystyle{ \mathcal{L} }[/math]. If such an approximation exists, one can construct a homotopy [math]\displaystyle{ H }[/math] transforming [math]\displaystyle{ f }[/math] into [math]\displaystyle{ g }[/math] by defining it on each simplex; there it always exists, because simplices are contractible.
The simplicial approximation theorem guarantees for every continuous function [math]\displaystyle{ f:V_K \rightarrow V_L }[/math] the existence of a simplicial approximation at least after refinement of [math]\displaystyle{ \mathcal{K} }[/math], for instance by replacing [math]\displaystyle{ \mathcal{K} }[/math] by its iterated barycentric subdivision.[2] The theorem plays an important role for certain statements in algebraic topology in order to reduce the behavior of continuous maps on those of simplicial maps, for instance in Lefschetz's fixed-point theorem.
Lefschetz's fixed-point theorem
The Lefschetz number is a useful tool to find out whether a continuous function admits fixed-points. This data is computed as follows: Suppose that [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are topological spaces that admit finite triangulations. A continuous map [math]\displaystyle{ f: X\rightarrow Y }[/math] induces homomorphisms [math]\displaystyle{ f_i: H_i(X,K)\rightarrow H_i(Y,K) }[/math] between its simplicial homology groups with coefficients in a field [math]\displaystyle{ K }[/math]. These are linear maps between [math]\displaystyle{ K }[/math]- vectorspaces, so their trace [math]\displaystyle{ tr_i }[/math] can be determined and their alternating sum
[math]\displaystyle{ L_K(f)= \sum_i(-1)^itr_i(f) \in K }[/math]
is called the Lefschetz number of [math]\displaystyle{ f }[/math]. If [math]\displaystyle{ f = id }[/math], this number is the Euler characteristic of [math]\displaystyle{ K }[/math]. The fixpoint theorem states that whenever [math]\displaystyle{ L_K(f)\neq 0 }[/math], [math]\displaystyle{ f }[/math] has a fixed-point. In the proof this is first shown only for simplicial maps and then generalized for any continuous functions via the approximation theorem. Brouwer's fixpoint theorem treats the case where [math]\displaystyle{ f:\mathbb{D}^n \rightarrow \mathbb{D}^n }[/math] is an endomorphism of the unit-ball. For [math]\displaystyle{ k \geq 1 }[/math] all its homology groups [math]\displaystyle{ H_k(\mathbb{D}^n) }[/math] vanishes, and [math]\displaystyle{ f_0 }[/math] is always the identity, so [math]\displaystyle{ L_K(f) = tr_0(f) = 1 \neq 0 }[/math], so [math]\displaystyle{ f }[/math] has a fixpoint.[20]
Formula of Riemann-Hurwitz
The Riemann- Hurwitz formula allows to determine the gender of a compact, connected Riemann surface [math]\displaystyle{ X }[/math] without using explicit triangulation. The proof needs the existence of triangulations for surfaces in an abstract sense: Let [math]\displaystyle{ F:X \rightarrow Y }[/math] be a non-constant holomorphic function on a surface with known gender. The relation between the gender [math]\displaystyle{ g }[/math] of the surfaces [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] is
[math]\displaystyle{ 2g(X)-2= deg(F)(2g(Y)-2) \sum_{x\in X}(ord(F)-1) }[/math]
where [math]\displaystyle{ deg(F) }[/math] denotes the degree of the map. The sum is well defined as it counts only the ramifying points of the function.
The background of this formula is that holomorphic functions on Riemann surfaces are ramified coverings. The formula can be found by examining the image of the simplicial structure near to ramifiying points.[21]
Citations
- ↑ 1.0 1.1 John M. Lee (2000) (in German), Introduction to Topological manifolds, New York/Berlin/Heidelberg: Springer Verlag, p. 92, ISBN 0-387-98759-2
- ↑ 2.0 2.1 2.2 2.3 2.4 James R. Munkres (1984) (in German), Elements of algebraic topology, 1984, Menlo Park, California: Addison Wesley, p. 83, ISBN 0-201-04586-9
- ↑ 3.0 3.1 J. H. C. Whitehead (1940), "On C1-Complexes" (in German), Annals of Mathematics 41 (4): pp. 809–824, doi:10.2307/1968861, ISSN 0003-486X
- ↑ J. W. Alexander (1926), "Combinatorial Analysis Situs" (in German), Transactions of the American Mathematical Society 28 (2): pp. 301–329, doi:10.1090/S0002-9947-1926-1501346-5, ISSN 0002-9947
- ↑ R. Stöcker, H. Zieschang (1994) (in German), Algebraische Topologie (2. überarbeitete ed.), Stuttgart: B.G.Teubner, p. 270, ISBN 3-519-12226-X
- ↑ 6.0 6.1 Allen Hatcher (2006) (in German), Algebraic Topologie, Cambridge/New York/Melbourne: Cambridge University Press, p. 110, ISBN 0-521-79160--X
- ↑ A.A.Ranicki. "One the Hauptvermutung". https://www.maths.ed.ac.uk/~v1ranick/books/haupt.pdf.
- ↑ 8.0 8.1 John Milnor (1961), "Two Complexes Which are Homeomorphic But Combinatorially Distinct" (in German), The Annals of Mathematics 74 (3): p. 575, doi:10.2307/1970299, ISSN 0003-486X
- ↑ Marshall M. Cohen (1973), "A Course in Simple-Homotopy Theory" (in German), Graduate Texts in Mathematics, Graduate Texts in Mathematics 10, doi:10.1007/978-1-4684-9372-6, ISBN 978-0-387-90055-1, ISSN 0072-5285
- ↑ Edwin Moise (1977) (in German), Geometric Topology in Dimensions 2 and 3, New York: Springer Verlag
- ↑ Tibor Rado. "Über den Begriff der Riemannschen Fläche". https://www.maths.ed.ac.uk/~v1ranick/papers/rado.pdf.
- ↑ R. C. Kirby, L. C. Siebenmann (1977-12-31), "Annex B. On The Triangulation of Manifolds and the Hauptvermutung" (in German), Foundational Essays on Topological Manifolds, Smoothings, and Triangulations. (AM-88) (Princeton University Press): pp. 299–306
- ↑ "Chapter IV; Casson's Invariant for Oriented Homology 3-spheres" (in German), Casson's Invariant for Oriented Homology Three-Spheres (Princeton University Press): pp. 63–79, 1990-12-31
- ↑ Toenniessen, Fridtjof (2017) (in German), Topologie, doi:10.1007/978-3-662-54964-3, ISBN 978-3-662-54963-6, https://link.springer.com/content/pdf/10.1007/978-3-662-54964-3.pdf, retrieved 2022-04-20
- ↑ Edwin E. Moise (1952), "Affine Structures in 3-Manifolds: V. The Triangulation Theorem and Hauptvermutung" (in German), The Annals of Mathematics 56 (1): p. 96, doi:10.2307/1969769, ISSN 0003-486X
- ↑ Robert D. Edwards (2006-10-18), "Suspensions of homology spheres" (in German), arXiv:math/0610573, Bibcode: 2006math.....10573E
- ↑ W B R Lickorish (1999-11-20), "Simplicial moves on complexes and manifolds" (in German), Proceedings of the Kirbyfest (Mathematical Sciences Publishers), doi:10.2140/gtm.1999.2.299
- ↑ Toenniessen, Fridtjof (2017) (in German), Topologie, p. 315, doi:10.1007/978-3-662-54964-3, ISBN 978-3-662-54963-6, https://link.springer.com/content/pdf/10.1007/978-3-662-54964-3.pdf, retrieved 2022-04-20
- ↑ Seifert, H. (Herbert), 1907-1996. (2003) (in German), Lehrbuch der Topologie, AMS Chelsea Pub., ISBN 0-8218-3595-5
- ↑ Bredon, Glen E. (1993) (in German), Topology and Geometry, Berlin/ Heidelberg/ New York, pp. 254 f, ISBN 3-540-97926-3
- ↑ Otto Forster (1977), "Kompakte Riemannsche Flächen" (in German), Heidelberger Taschenbücher (Berlin, Heidelberg: Springer Berlin Heidelberg): pp. 88–154, ISBN 978-3-540-08034-3
See also
Literature
- Allen Hatcher: Algebraic Topology, Cambridge University Press, Cambridge/New York/Melbourne 2006, ISBN 0-521-79160-X
- James R. Munkres: . Band 1984. Addison Wesley, Menlo Park, California 1984, ISBN 0-201-04586-9
- Marshall M. Cohen: A course in Simple-Homotopy Theory . In: Graduate Texts in Mathematics. 1973, ISSN 0072-5285, doi:10.1007/978-1-4684-9372-6.
 |