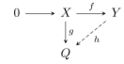Glossary of module theory
From HandWiki
Short description: none
Module theory is the branch of mathematics in which modules are studied. This is a glossary of some terms of the subject.
See also: Glossary of linear algebra, Glossary of ring theory, Glossary of representation theory.
A
- algebraically compact
- algebraically compact module (also called pure injective module) is a module in which all systems of equations can be decided by finitary means. Alternatively, those modules which leave pure-exact sequence exact after applying Hom.
- annihilator
- 1. The annihilator of a left [math]\displaystyle{ R }[/math]-module [math]\displaystyle{ M }[/math] is the set [math]\displaystyle{ \textrm{Ann}(M) := \{ r \in R ~|~ rm = 0 \, \forall m \in M \} }[/math] . It is a (left) ideal of [math]\displaystyle{ R }[/math].
- 2. The annihilator of an element [math]\displaystyle{ m \in M }[/math] is the set [math]\displaystyle{ \textrm{Ann}(m) := \{ r \in R ~|~ rm = 0 \} }[/math].
- Artinian
- An Artinian module is a module in which every decreasing chain of submodules becomes stationary after finitely many steps.
- associated prime
- 1. associated prime
- automorphism
- An automorphism is an endomorphism that is also an isomorphism.
- Azumaya
- Azumaya's theorem says that two decompositions into modules with local endomorphism rings are equivalent.
B
- balanced
- balanced module
- basis
- A basis of a module [math]\displaystyle{ M }[/math] is a set of elements in [math]\displaystyle{ M }[/math] such that every element in the module can be expressed as a finite sum of elements in the basis in a unique way.
- Beauville–Laszlo
- Beauville–Laszlo theorem
- big
- "big" usually means "not-necessarily finitely generated".
- bimodule
- bimodule
C
- canonical module
- canonical module (the term "canonical" comes from canonical divisor)
- category
- The category of modules over a ring is the category where the objects are all the (say) left modules over the given ring and the morphisms module homomorphisms.
- character
- character module
- chain complex
- chain complex (frequently just complex)
- closed submodule
- A module is called a closed submodule if it does not contain any essential extension.
- Cohen–Macaulay
- Cohen–Macaulay module
- coherent
- A coherent module is a finitely generated module whose finitely generated submodules are finitely presented.
- cokernel
- The cokernel of a module homomorphism is the codomain quotiented by the image.
- compact
- A compact module
- completely reducible
- Synonymous to "semisimple module".
- completion
- completion of a module
- composition
- Jordan Hölder composition series
- continuous
- continuous module
- countably generated
- A countably generated module is a module that admits a generating set whose cardinality is at most countable.
- cyclic
- A module is called a cyclic module if it is generated by one element.
D
- D
- A D-module is a module over a ring of differential operators.
- decomposition
- A decomposition of a module is a way to express a module as a direct sum of submodules.
- dense
- dense submodule
- determinant
- The determinant of a finite free module over a commutative ring is the r-th exterior power of the module when r is the rank of the module.
- differential
- A differential graded module or dg-module is a graded module with a differential.
- direct sum
- A direct sum of modules is a module that is the direct sum of the underlying abelian group together with component-wise scalar multiplication.
- dual module
- The dual module of a module M over a commutative ring R is the module [math]\displaystyle{ \operatorname{Hom}_R(M, R) }[/math].
- dualizing
- dualizing module
- Drinfeld
- A Drinfeld module is a module over a ring of functions on algebraic curve with coefficients from a finite field.
E
- Eilenberg–Mazur
- Eilenberg–Mazur swindle
- elementary
- elementary divisor
- endomorphism
- 1. An endomorphism is a module homomorphism from a module to itself.
- 2. The endomorphism ring is the set of all module homomorphisms with addition as addition of functions and multiplication composition of functions.
- enough
- enough injectives
- enough projectives
- essential
- Given a module M, an essential submodule N of M is a submodule that every nonzero submodule of M intersects non-trivially.
- exact
- exact sequence
- Ext functor
- Ext functor
- extension
- Extension of scalars uses a ring homomorphism from R to S to convert R-modules to S-modules.
F
- faithful
- A faithful module [math]\displaystyle{ M }[/math] is one where the action of each nonzero [math]\displaystyle{ r \in R }[/math] on [math]\displaystyle{ M }[/math] is nontrivial (i.e. [math]\displaystyle{ rx \ne 0 }[/math] for some [math]\displaystyle{ x }[/math] in [math]\displaystyle{ M }[/math]). Equivalently, [math]\displaystyle{ \textrm{Ann}(M) }[/math] is the zero ideal.
- finite
- The term "finite module" is another name for a finitely generated module.
- finite length
- A module of finite length is a module that admits a (finite) composition series.
- finite presentation
- 1. A finite free presentation of a module M is an exact sequence [math]\displaystyle{ F_1 \to F_0 \to M }[/math] where [math]\displaystyle{ F_i }[/math] are finitely generated free modules.
- 2. A finitely presented module is a module that admits a finite free presentation.
- finitely generated
- A module [math]\displaystyle{ M }[/math] is finitely generated if there exist finitely many elements [math]\displaystyle{ x_1,...,x_n }[/math] in [math]\displaystyle{ M }[/math] such that every element of [math]\displaystyle{ M }[/math] is a finite linear combination of those elements with coefficients from the scalar ring [math]\displaystyle{ R }[/math].
- fitting
- 1. fitting ideal
- 2. Fitting's lemma
- five
- Five lemma
- flat
- A [math]\displaystyle{ R }[/math]-module [math]\displaystyle{ F }[/math] is called a flat module if the tensor product functor [math]\displaystyle{ - \otimes_R F }[/math] is exact.In particular, every projective module is flat.
- free
- A free module is a module that has a basis, or equivalently, one that is isomorphic to a direct sum of copies of the scalar ring [math]\displaystyle{ R }[/math].
- Frobenius reciprocity
- Frobenius reciprocity.
G
- Galois
- A Galois module is a module over the group ring of a Galois group.
- generating set
- A subset of a module is called a generating set of the module if the submodule generated by the set (i.e., the smallest subset containing the set) is the entire module itself.
- global
- global dimension
- graded
- A module [math]\displaystyle{ M }[/math] over a graded ring [math]\displaystyle{ A = \bigoplus_{n\in \mathbb N}A_n }[/math] is a graded module if [math]\displaystyle{ M }[/math] can be expressed as a direct sum [math]\displaystyle{ \bigoplus_{i\in \mathbb N}M_i }[/math] and [math]\displaystyle{ A_i M_j \subseteq M_{i+j} }[/math].
H
- Herbrand quotient
- A Herbrand quotient of a module homomorphism is another term for index.
- Hilbert
- 1. Hilbert's syzygy theorem
- 2. The Hilbert–Poincaré series of a graded module.
- 3. The Hilbert–Serre theorem tells when a Hilbert–Poincaré series is a rational function.
- homological dimension
- homological dimension
- homomorphism
- For two left [math]\displaystyle{ R }[/math]-modules [math]\displaystyle{ M_1, M_2 }[/math], a group homomorphism [math]\displaystyle{ \phi: M_1 \to M_2 }[/math] is called homomorphism of [math]\displaystyle{ R }[/math]-modules if [math]\displaystyle{ r \phi(m) = \phi (r m) \, \forall r \in R, m \in M_1 }[/math] .
- Hom
- Hom functor
I
- idempotent
- An idempotent is an endomorphism whose square is itself.
- indecomposable
- An indecomposable module is a non-zero module that cannot be written as a direct sum of two non-zero submodules. Every simple module is indecomposable (but not conversely).
- index
- The index of an endomorphism [math]\displaystyle{ f : M \to M }[/math] is the difference [math]\displaystyle{ \operatorname{length}(\operatorname{coker}(f)) - \operatorname{length}(\operatorname{ker}(f)) }[/math], when the cokernel and kernel of [math]\displaystyle{ f }[/math] have finite length.
- injective
- 1. A [math]\displaystyle{ R }[/math]-module [math]\displaystyle{ Q }[/math] is called an injective module if given a [math]\displaystyle{ R }[/math]-module homomorphism [math]\displaystyle{ g:
X \to Q }[/math], and an injective [math]\displaystyle{ R }[/math]-module homomorphism [math]\displaystyle{ f: X \to Y }[/math], there exists a
[math]\displaystyle{ R }[/math]-module homomorphism [math]\displaystyle{ h : Y \to Q }[/math] such that [math]\displaystyle{ f \circ h = g }[/math].
- The following conditions are equivalent:
- The contravariant functor [math]\displaystyle{ \textrm{Hom}_R( - , I) }[/math] is exact.
- [math]\displaystyle{ I }[/math] is a injective module.
- Every short exact sequence [math]\displaystyle{ 0 \to I \to L \to L' \to 0 }[/math] is split.
- The following conditions are equivalent:
J
- Jacobson
- density theorem
K
- Kähler differentials
- Kähler differentials
- Kaplansky
- Kaplansky's theorem on a projective module says that a projective module over a local ring is free.
- kernel
- The kernel of a module homomorphism is the pre-image of the zero element.
- Koszul complex
- Koszul complex
- Krull–Schmidt
- The Krull–Schmidt theorem says that (1) a finite-length module admits an indecomposable decomposition and (2) any two indecomposable decompositions of it are equivalent.
L
- length
- The length of a module is the common length of any composition series of the module; the length is infinite if there is no composition series. Over a field, the length is more commonly known as the dimension.
- linear
- 1. A linear map is another term for a module homomorphism.
- 2. Linear topology
- localization
- Localization of a module converts R modules to S modules, where S is a localization of R.
M
- Matlis module
- Matlis module
- Mitchell's embedding theorem
- Mitchell's embedding theorem
- Mittag-Leffler
- Mittag-Leffler condition (ML)
- module
- 1. A left module [math]\displaystyle{ M }[/math] over the ring [math]\displaystyle{ R }[/math] is an abelian group [math]\displaystyle{ (M, +) }[/math] with an operation [math]\displaystyle{ R \times M \to M }[/math] (called scalar multipliction) satisfies the following condition:
- [math]\displaystyle{ \forall r,s \in R, \forall m,n \in M }[/math],
- [math]\displaystyle{ r (m + n) = rm + rn }[/math]
- [math]\displaystyle{ r (s m) = (r s) m }[/math]
- [math]\displaystyle{ 1_R \, m = m }[/math]
- [math]\displaystyle{ \forall r,s \in R, \forall m,n \in M }[/math],
- [math]\displaystyle{ (m + n) r = m r + n r }[/math]
- [math]\displaystyle{ (m s) r = r (s m) }[/math]
- [math]\displaystyle{ m 1_R = m }[/math]
N
- nilpotent
- A nilpotent endomorphism is an endomorphism, some power of which is zero.
- Noetherian
- A Noetherian module is a module such that every submodule is finitely generated. Equivalently, every increasing chain of submodules becomes stationary after finitely many steps.
- normal
- normal forms for matrices
P
- perfect
- 1. perfect complex
- 2. perfect module
- principal
- A principal indecomposable module is a cyclic indecomposable projective module.
- primary
- primary submodule
- projective
- A [math]\displaystyle{ R }[/math]-module [math]\displaystyle{ P }[/math] is called a projective module if given a [math]\displaystyle{ R }[/math]-module homomorphism [math]\displaystyle{ g: P \to M }[/math], and a surjective [math]\displaystyle{ R }[/math]-module homomorphism [math]\displaystyle{ f: N \to M }[/math], there exists a [math]\displaystyle{ R }[/math]-module homomorphism [math]\displaystyle{ h : P \to N }[/math] such that [math]\displaystyle{ f \circ h = g }[/math].
 The characteristic property of projective modules is called lifting.
The characteristic property of projective modules is called lifting.- The following conditions are equivalent:
- The covariant functor [math]\displaystyle{ \textrm{Hom}_R(P, - ) }[/math] is exact.
- [math]\displaystyle{ M }[/math] is a projective module.
- Every short exact sequence [math]\displaystyle{ 0 \to L \to L' \to P \to 0 }[/math] is split.
- [math]\displaystyle{ M }[/math] is a direct summand of free modules.
- In particular, every free module is projective.
- The following conditions are equivalent:
Q
- Quillen–Suslin theorem
- The Quillen–Suslin theorem states that a finite projective module over a polynomial ring is free.
- quotient
- Given a left [math]\displaystyle{ R }[/math]-module [math]\displaystyle{ M }[/math] and a submodule [math]\displaystyle{ N }[/math], the quotient group [math]\displaystyle{ M/N }[/math] can be made to be a left [math]\displaystyle{ R }[/math]-module by [math]\displaystyle{ r(m+N) = rm + N }[/math] for [math]\displaystyle{ r \in R, \, m \in M }[/math]. It is called a quotient module or factor module.
R
- radical
- The radical of a module is the intersection of the maximal submodules. For Artinian modules, the smallest submodule with semisimple quotient.
- rational
- rational canonical form
- reflexive
- A reflexive module is a module that is isomorphic via the natural map to its second dual.
- resolution
- resolution
- restriction
- Restriction of scalars uses a ring homomorphism from R to S to convert S-modules to R-modules.
S
- Schanuel
- Schanuel's lemma
- Schur
- Schur's lemma says that the endomorphism ring of a simple module is a division ring.
- Shapiro
- Shapiro's lemma
- sheaf of modules
- sheaf of modules
- snake
- snake lemma
- socle
- The socle is the largest semisimple submodule.
- semisimple
- A semisimple module is a direct sum of simple modules.
- simple
- A simple module is a nonzero module whose only submodules are zero and itself.
- Smith
- Smith normal form
- stably free
- A stably free module
- structure theorem
- The structure theorem for finitely generated modules over a principal ideal domain says that a finitely generated modules over PIDs are finite direct sums of primary cyclic modules.
- submodule
- Given a [math]\displaystyle{ R }[/math]-module [math]\displaystyle{ M }[/math], an additive subgroup [math]\displaystyle{ N }[/math] of [math]\displaystyle{ M }[/math] is a submodule if [math]\displaystyle{ RN \subset N }[/math].
- support
- The support of a module over a commutative ring is the set of prime ideals at which the localizations of the module are nonzero.
T
- tensor
- Tensor product of modules
- topological
- A topological module
- Tor
- Tor functor
- torsion-free
- torsion-free module
- torsionless
- torsionless module
U
- uniform
- A uniform module is a module in which every two non-zero submodules have a non-zero intersection.
W
- weak
- weak dimension
Z
- zero
- 1. The zero module is a module consisting of only zero element.
- 2. The zero module homomorphism is a module homomorphism that maps every element to zero.
References
- John A. Beachy (1999). Introductory Lectures on Rings and Modules (1st ed.). Addison-Wesley. ISBN 0-521-64407-0. https://archive.org/details/introductorylect0000beac.
- Golan, Jonathan S.; Head, Tom (1991), Modules and the structure of rings, Monographs and Textbooks in Pure and Applied Mathematics, 147, Marcel Dekker, ISBN 978-0-8247-8555-0, https://archive.org/details/modulesstructure0000gola
- Lam, Tsit-Yuen (1999), Lectures on modules and rings, Graduate Texts in Mathematics No. 189, Berlin, New York: Springer-Verlag, ISBN 978-0-387-98428-5
- Serge Lang (1993). Algebra (3rd ed.). Addison-Wesley. ISBN 0-201-55540-9.
- Passman, Donald S. (1991), A course in ring theory, The Wadsworth & Brooks/Cole Mathematics Series, Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software, ISBN 978-0-534-13776-2
 |