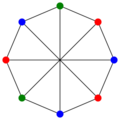
Wagner graph
| Wagner graph | |
|---|---|
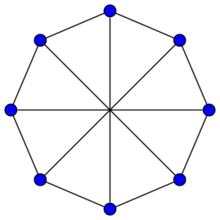 The Wagner graph | |
| Named after | Klaus Wagner |
| Vertices | 8 |
| Edges | 12 |
| Radius | 2 |
| Diameter | 2 |
| Girth | 4 |
| Automorphisms | 16 (D8) |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Genus | 1 |
| Spectrum | [math]\displaystyle{ \begin{pmatrix}3 & 1 & \sqrt{2}-1 & -1 & -\sqrt{2}-1 \\1 & 2 & 2 & 1 & 2 \end{pmatrix} }[/math] |
| Properties | Cubic Hamiltonian Triangle-free Vertex-transitive Toroidal Apex |
| Notation | M8 |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Wagner graph is a 3-regular graph with 8 vertices and 12 edges.[1] It is the 8-vertex Möbius ladder graph.
Properties
As a Möbius ladder, the Wagner graph is nonplanar but has crossing number one, making it an apex graph. It can be embedded without crossings on a torus or projective plane, so it is also a toroidal graph. It has girth 4, diameter 2, radius 2, chromatic number 3, chromatic index 3 and is both 3-vertex-connected and 3-edge-connected.
The Wagner graph has 392 spanning trees; it and the complete bipartite graph K3,3 have the most spanning trees among all cubic graphs with the same number of vertices.[2]
The Wagner graph is a vertex-transitive graph but is not edge-transitive. Its full automorphism group is isomorphic to the dihedral group D8 of order 16, the group of symmetries of an octagon, including both rotations and reflections.
The characteristic polynomial of the Wagner graph is
- [math]\displaystyle{ (x-3)(x-1)^2(x+1)(x^2+2x-1)^2. }[/math]
It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
The Wagner graph is triangle-free and has independence number three, providing one half of the proof that the Ramsey number R(3,4) (the least number n such that any n-vertex graph contains either a triangle or a four-vertex independent set) is 9.[3]
Graph minors
Möbius ladders play an important role in the theory of graph minors. The earliest result of this type is a 1937 theorem of Klaus Wagner (part of a cluster of results known as Wagner's theorem) that graphs with no K5 minor can be formed by using clique-sum operations to combine planar graphs and the Möbius ladder M8.[4] For this reason M8 is called the Wagner graph.
The Wagner graph is also one of four minimal forbidden minors for the graphs of treewidth at most three (the other three being the complete graph K5, the graph of the regular octahedron, and the graph of the pentagonal prism) and one of four minimal forbidden minors for the graphs of branchwidth at most three (the other three being K5, the graph of the octahedron, and the cube graph).[5][6]
Construction
The Wagner graph is a cubic Hamiltonian graph and can be defined by the LCF notation [4]8. It is an instance of an Andrásfai graph, a type of circulant graph in which the vertices can be arranged in a cycle and each vertex is connected to the other vertices whose positions differ by a number that is 1 (mod 3). It is also isomorphic to the circular clique K8/3.
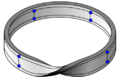
It can be drawn as a ladder graph with 4 rungs made cyclic on a topological Möbius strip.
Gallery
The chromatic number of the Wagner graph is 3.
References
- ↑ Bondy, J. A.; Murty, U. S. R. (2007). Graph Theory. Springer. pp. 275–276. ISBN 978-1-84628-969-9.
- ↑ Jakobson, Dmitry; Rivin, Igor (1999). "On some extremal problems in graph theory". arXiv:math.CO/9907050.
- ↑ Soifer, Alexander (2008). The Mathematical Coloring Book. Springer-Verlag. p. 245. ISBN 978-0-387-74640-1.
- ↑ Wagner, K. (1937). "Über eine Eigenschaft der ebenen Komplexe" (in German). Mathematische Annalen 114 (1): 570–590. doi:10.1007/BF01594196.
- ↑ Bodlaender, Hans L. (1998). "A partial k-arboretum of graphs with bounded treewidth". Theoretical Computer Science 209 (1–2): 1–45. doi:10.1016/S0304-3975(97)00228-4.
- ↑ Bodlaender, Hans L.; Thilikos, Dimitrios M. (1999). "Graphs with branchwidth at most three". Journal of Algorithms 32 (2): 167–194. doi:10.1006/jagm.1999.1011.
 |