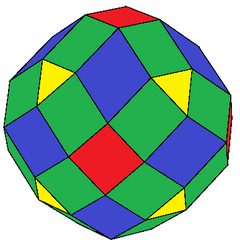
Expanded cuboctahedron
| Expanded cuboctahedron | |
|---|---|
| |
| Schläfli symbol | rr[math]\displaystyle{ \begin{Bmatrix} 4 \\ 3 \end{Bmatrix} }[/math] = rrr{4,3} |
| Conway notation | edaC = aaaC |
| Faces | 50: 8 {3} 6+24 {4} 12 rhombs |
| Edges | 96 |
| Vertices | 48 |
| Symmetry group | Oh, [4,3], (*432) order 48 |
| Rotation group | O, [4,3]+, (432), order 24 |
| Dual polyhedron | Deltoidal tetracontaoctahedron
|
| Properties | convex |
 Net | |
The expanded cuboctahedron is a polyhedron constructed by expansion of the cuboctahedron. It has 50 faces: 8 triangles, 30 squares, and 12 rhombs. The 48 vertices exist at two sets of 24, with a slightly different distance from its center.
It can also be constructed as a rectified rhombicuboctahedron.
Other names
- Expanded rhombic dodecahedron
- Rectified rhombicuboctahedron
- Rectified small rhombicuboctahedron
- Rhombirhombicuboctahedron
- Expanded expanded tetrahedron
Expansion
The expansion operation from the rhombic dodecahedron can be seen in this animation:
Honeycomb
The expanded cuboctahedron can fill space along with a cuboctahedron, octahedron, and triangular prism.
Dissection
| Excavated expanded cuboctahedron | |
|---|---|
| Faces | 86: 8 {3} 6+24+48 {4} |
| Edges | 168 |
| Vertices | 62 |
| Euler characteristic | -20 |
| genus | 11 |
| Symmetry group | Oh, [4,3], (*432) order 48 |
This polyhedron can be dissected into a central rhombic dodecahedron surrounded by: 12 rhombic prisms, 8 tetrahedra, 6 square pyramids, and 24 triangular prisms.
If the central rhombic dodecahedron and the 12 rhombic prisms are removed, you can create a toroidal polyhedron with all regular polygon faces.[1] This toroid has 86 faces (8 triangles and 78 squares), 168 edges, and 62 vertices. 14 of the 62 vertices are on the interior, defining the removed central rhombic dodecahedron. With Euler characteristic χ = f + v - e = -20, its genus, g = (2-χ)/2 is 11.
Related polyhedra
| Name | Cube | Cubocta- hedron |
Rhombi- cuboctahedron |
Expanded cuboctahedron |
|---|---|---|---|---|
| Coxeter[2] | C | CO = rC | rCO = rrC | rrCO = rrrC |
| Conway | aC = aO | eC | eaC | |
| Image | 
|

|

|

|
| Conway | O = dC | jC | oC | oaC |
| Dual | 
|
|

|

|
See also
References
- Coxeter Regular Polytopes, Third edition, (1973), Dover edition, ISBN:0-486-61480-8 (pp. 145–154 Chapter 8: Truncation)
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN:978-1-56881-220-5
External links
- George Hart's Conway interpreter: generates polyhedra in VRML, taking Conway notation as input
- Variations on a Rhombic Theme
- www.software3d.com: Prism-Expanded Dissected Cuboctahedron
 |




