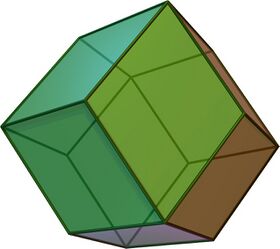
Rhombic dodecahedron

Short description: Catalan solid with 12 faces

Rhombic dodecahedron
(Click here for rotating model)
Type	Catalan solid
Coxeter diagram
Conway notation	jC
Face type	V3.4.3.4 rhombus
Faces	12
Edges	24
Vertices	14
Vertices by type	8{3}+6{4}
Symmetry group	O_h, B₃, [4,3], (*432)
Rotation group	O, [4,3]⁺, (432)
Dihedral angle	120°
Properties	convex, face-transitive isohedral, isotoxal, parallelohedron
Cuboctahedron (dual polyhedron)	Net

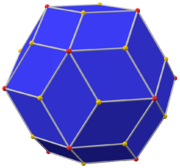
File:Rhombic dodecahedron.stl In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron.

Properties

The rhombic dodecahedron is a zonohedron. Its polyhedral dual is the cuboctahedron. The long face-diagonal length is exactly √2 times the short face-diagonal length; thus, the acute angles on each face measure arccos(1/3), or approximately 70.53°.

Being the dual of an Archimedean polyhedron, the rhombic dodecahedron is face-transitive, meaning the symmetry group of the solid acts transitively on its set of faces. In elementary terms, this means that for any two faces A and B, there is a rotation or reflection of the solid that leaves it occupying the same region of space while moving face A to face B.

The rhombic dodecahedron can be viewed as the convex hull of the union of the vertices of a cube and an octahedron. The 6 vertices where 4 rhombi meet correspond to the vertices of the octahedron, while the 8 vertices where 3 rhombi meet correspond to the vertices of the cube.

The rhombic dodecahedron is one of the nine edge-transitive convex polyhedra, the others being the five Platonic solids, the cuboctahedron, the icosidodecahedron, and the rhombic triacontahedron.

The rhombic dodecahedron can be used to tessellate three-dimensional space: it can be stacked to fill a space, much like hexagons fill a plane.

This polyhedron in a space-filling tessellation can be seen as the Voronoi tessellation of the face-centered cubic lattice. It is the Brillouin zone of body centered cubic (bcc) crystals. Some minerals such as garnet form a rhombic dodecahedral crystal habit. As Johannes Kepler noted in his 1611 book on snowflakes (Strena seu de Nive Sexangula), honey bees use the geometry of rhombic dodecahedra to form honeycombs from a tessellation of cells each of which is a hexagonal prism capped with half a rhombic dodecahedron. The rhombic dodecahedron also appears in the unit cells of diamond and diamondoids. In these cases, four vertices (alternate threefold ones) are absent, but the chemical bonds lie on the remaining edges.^[1]

The graph of the rhombic dodecahedron is nonhamiltonian.

A rhombic dodecahedron can be dissected into 4 obtuse trigonal trapezohedra around its center. These rhombohedra are the cells of a trigonal trapezohedral honeycomb. Analogy: a regular hexagon can be dissected into 3 rhombi around its center. These rhombi are the tiles of a rhombille.

The collections of the Louvre include a die in the shape of a rhombic dodecahedron dating from Ptolemaic Egypt. The faces are inscribed with Greek letters representing the numbers 1 through 12: Α Β Γ Δ Ε Ϛ Z Η Θ Ι ΙΑ ΙΒ. The function of the die is unknown.^[2]

Rhombic dodecahedron dissected into 4 rhombohedra
Hexagon dissected into 3 rhombi
A garnet crystal
This animation shows the construction of a rhombic dodecahedron from a cube, by inverting the center-face-pyramids of a cube.

Dimensions

Denoting by a the edge length of a rhombic dodecahedron,

the radius of its inscribed sphere (tangent to each of the rhombic dodecahedron's faces) is

[math]\displaystyle{ r_\mathrm{i} = \frac{\sqrt{6}}{3}~a \approx 0.816\,496\,5809~a\quad }[/math] (OEIS: A157697),

the radius of its midsphere is

[math]\displaystyle{ r_\mathrm{m} = \frac{2\sqrt{2}}{3}~a \approx 0.942\,809\,041\,58~a\quad }[/math] (OEIS: A179587),

the radius of the sphere passing through the six order 4 vertices, but not through the eight order 3 vertices, is

[math]\displaystyle{ r_\mathrm{o} = \frac{2\sqrt{3}}{3}~a \approx 1.154\,700\,538~a\quad }[/math] (OEIS: A020832),

the radius of the sphere passing through the eight order 3 vertices is exactly equal to the length of the sides

[math]\displaystyle{ r_\mathrm{t} = a }[/math]

Area and volume

The surface area A and the volume V of the rhombic dodecahedron with edge length a are:

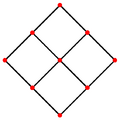
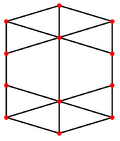
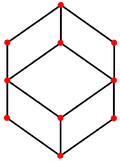
[math]\displaystyle{ A = 8\sqrt{2}~a^2 \approx 11.313\,7085~a^2 }[/math]

[math]\displaystyle{ V = \frac{16\sqrt{3}}{9}~a^3 \approx 3.079\,201\,44~a^3 }[/math]

Orthogonal projections

The rhombic dodecahedron has four special orthogonal projections along its axes of symmetry, centered on a face, an edge, and the two types of vertex, threefold and fourfold. The last two correspond to the B₂ and A₂ Coxeter planes.

Orthogonal projections
Projective symmetry	[4]	[6]	[2]	[2]
Rhombic dodecahedron
Cuboctahedron (dual)

Cartesian coordinates

Pyritohedron variations between a cube and rhombic dodecahedron	Expansion of a rhombic dodecahedron

For edge length √3, the eight vertices where three faces meet at their obtuse angles have Cartesian coordinates:

(±1, ±1, ±1)

The coordinates of the six vertices where four faces meet at their acute angles are:

(±2, 0, 0), (0, ±2, 0) and (0, 0, ±2)

The rhombic dodecahedron can be seen as a degenerate limiting case of a pyritohedron, with permutation of coordinates (±1, ±1, ±1) and (0, 1 + h, 1 − h²) with parameter h = 1.

These coordinates illustrate that a rhombic dodecahedron can be seen as a cube with a square pyramid attached to each face, and that the six square pyramids could fit together to a cube of the same size, i.e the rhombic dodecahedron has twice the volume of the inscribed cube with edges equal to the short diagonals of the rhombi.^[3]

Topologically equivalent forms

A topological rhombic dodecahedron can be seen inside of a hexagonal prism, with hexagons dissected into rhombi in complementary ways between top and bottom.

Parallelohedron

The rhombic dodecahedron is a parallelohedron, a space-filling polyhedron, dodecahedrille, being the dual to the tetroctahedrille or half cubic honeycomb, and described by two Coxeter diagrams: and . With D_3d symmetry, it can be seen as an elongated trigonal trapezohedron.

The rhombic dodecahedron can tessellate space by translational copies of itself, as can the stellated rhombic dodecahedron.	The rhombic dodecahedron can be constructed with 4 sets of 6 parallel edges.

Dihedral rhombic dodecahedron

Other symmetry constructions of the rhombic dodecahedron are also space-filling, and as parallelotopes they are similar to variations of space-filling truncated octahedra.^[4]

For example, with 4 square faces, and 60-degree rhombic faces, and D_4h dihedral symmetry, order 16. It can be seen as a cuboctahedron with square pyramids augmented on the top and bottom.

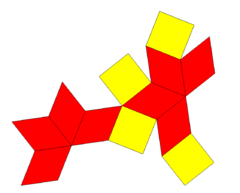	Net	Coordinates (0, 0, ±2) (±1, ±1, 0) (±1, 0, ±1) (0, ±1, ±1)

Bilinski dodecahedron

Main page: Bilinski dodecahedron

Bilinski dodecahedron with edges and front faces colored by their symmetry positions.	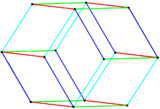Bilinski dodecahedron colored by parallel edges

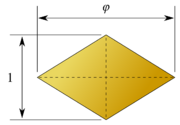
In 1960 Stanko Bilinski discovered a second rhombic dodecahedron with 12 congruent rhombus faces, the Bilinski dodecahedron. It has the same topology but different geometry. The rhombic faces in this form have the golden ratio.^[5]^[6]

Faces
First form	Second form

√2:1	√5 + 1/2:1

Deltoidal dodecahedron

Drawing and crystal model of deltoidal dodecahedron

Another topologically equivalent variation, sometimes called a deltoidal dodecahedron,^[7] is isohedral with tetrahedral symmetry order 24, distorting rhombic faces into kites (deltoids). It has 8 vertices adjusted in or out in alternate sets of 4, with the limiting case a tetrahedral envelope. Variations can be parametrized by (a,b), where b and a depend on each other such that the tetrahedron defined by the four vertices of a face has volume zero, i.e. is a planar face. (1,1) is the rhombic solution. As a approaches 1/2, b approaches infinity. It always holds that 1/a + 1/b = 2, with a, b > 1/2.

(±2, 0, 0), (0, ±2, 0), (0, 0, ±2)

(a, a, a), (−a, −a, a), (−a, a, −a), (a, −a, −a)

(−b, −b, −b), (−b, b, b), (b, −b, b), (b, b, −b)

(1,1)	(7/8,7/6)	(3/4,3/2)	(2/3,2)	(5/8,5/2)	(9/16,9/2)

Related polyhedra

Spherical rhombic dodecahedron

When projected onto a sphere (see right), it can be seen that the edges make up the edges of two tetrahedra arranged in their dual positions (the stella octangula). This trend continues on with the deltoidal icositetrahedron and deltoidal hexecontahedron for the dual pairings of the other regular polyhedra (alongside the triangular bipyramid if improper tilings are to be considered), giving this shape the alternative systematic name of deltoidal dodecahedron.

This polyhedron is a part of a sequence of rhombic polyhedra and tilings with [n,3] Coxeter group symmetry. The cube can be seen as a rhombic hexahedron where the rhombi are squares.

Similarly it relates to the infinite series of tilings with the face configurations V3.2n.3.2n, the first in the Euclidean plane, and the rest in the hyperbolic plane.

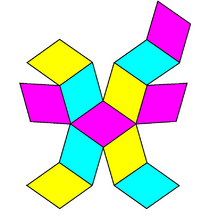V3.4.3.4 (Drawn as a net)	V3.6.3.6 Euclidean plane tiling Rhombille tiling	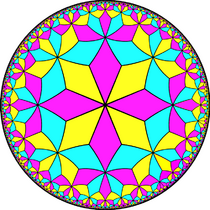V3.8.3.8 Hyperbolic plane tiling (Drawn in a Poincaré disk model)

Stellations

Like many convex polyhedra, the rhombic dodecahedron can be stellated by extending the faces or edges until they meet to form a new polyhedron. Several such stellations have been described by Dorman Luke.^[8]

This animation shows the construction of a stellated rhombic dodecahedron by inverting the center-face pyramids of a rhombic dodecahedron.

The first stellation, often simply called the stellated rhombic dodecahedron, is well known. It can be seen as a rhombic dodecahedron with each face augmented by attaching a rhombic-based pyramid to it, with a pyramid height such that the sides lie in the face planes of the neighbouring faces:

The first stellation of the rhombic dodecahedron
3D model of decomposition into 12 pyramids and 4 half-cubes

Luke describes four more stellations: the second and third stellations (expanding outwards), one formed by removing the second from the third, and another by adding the original rhombic dodecahedron back to the previous one.

Second	Third
Great stellated rhombic dodecahedron	Stellated rhombic dodecahedron

Related polytopes

In a perfect vertex-first projection two of the tesseract's vertices (marked in pale green) are projected exactly in the center of the rhombic dodecahedron

The rhombic dodecahedron forms the hull of the vertex-first projection of a tesseract to three dimensions. There are exactly two ways of decomposing a rhombic dodecahedron into four congruent rhombohedra, giving eight possible rhombohedra as projections of the tesseracts 8 cubic cells. One set of projective vectors are: u = (1,1,−1,−1), v = (−1,1,−1,1), w = (1,−1,−1,1).

The rhombic dodecahedron forms the maximal cross-section of a 24-cell, and also forms the hull of its vertex-first parallel projection into three dimensions. The rhombic dodecahedron can be decomposed into six congruent (but non-regular) square dipyramids meeting at a single vertex in the center; these form the images of six pairs of the 24-cell's octahedral cells. The remaining 12 octahedral cells project onto the faces of the rhombic dodecahedron. The non-regularity of these images are due to projective distortion; the facets of the 24-cell are regular octahedra in 4-space.

This decomposition gives an interesting method for constructing the rhombic dodecahedron: cut a cube into six congruent square pyramids, and attach them to the faces of a second cube. The triangular faces of each pair of adjacent pyramids lie on the same plane, and so merge into rhombuses. The 24-cell may also be constructed in an analogous way using two tesseracts.^[9]

Practical usage

In spacecraft reaction wheel layout, a tetrahedral configuration of four wheels is commonly used. For wheels that perform equally (from a peak torque and max angular momentum standpoint) in both spin directions and across all four wheels, the maximum torque and maximum momentum envelopes for the 3-axis attitude control system (considering idealized actuators) are given by projecting the tesseract representing the limits of each wheel's torque or momentum into 3D space via the 3 × 4 matrix of wheel axes; the resulting 3D polyhedron is a rhombic dodecahedron.^[10] Such an arrangement of reaction wheels is not the only possible configuration (a simpler arrangement consists of three wheels mounted to spin about orthogonal axes), but it is advantageous in providing redundancy to mitigate the failure of one of the four wheels (with degraded overall performance available from the remaining three active wheels) and in providing a more convex envelope than a cube, which leads to less agility dependence on axis direction (from an actuator/plant standpoint). Spacecraft mass properties influence overall system momentum and agility, so decreased variance in envelope boundary does not necessarily lead to increased uniformity in preferred axis biases (that is, even with a perfectly distributed performance limit within the actuator subsystem, preferred rotation axes are not necessarily arbitrary at the system level).

The polyhedron is also the basis for the HEALPix grid, used in cosmology for storing and manipulating maps of the cosmic microwave background, and in computer graphics for storing environment maps.