Quadrature of the Parabola

A parabolic segment.

Quadrature of the Parabola (Greek: Τετραγωνισμὸς παραβολῆς) is a treatise on geometry, written by Archimedes in the 3rd century BC and addressed to his Alexandrian acquaintance Dositheus. It contains 24 propositions regarding parabolas, culminating in two proofs showing that the area of a parabolic segment (the region enclosed by a parabola and a line) is [math]\displaystyle{ \tfrac43 }[/math] that of a certain inscribed triangle.

It is one of the best-known works of Archimedes, in particular for its ingenious use of the method of exhaustion and in the second part of a geometric series. Archimedes dissects the area into infinitely many triangles whose areas form a geometric progression. He then computes the sum of the resulting geometric series, and proves that this is the area of the parabolic segment. This represents the most sophisticated use of a reductio ad absurdum argument in ancient Greek mathematics, and Archimedes' solution remained unsurpassed until the development of integral calculus in the 17th century, being succeeded by Cavalieri's quadrature formula.

Main theorem

A parabolic segment is the region bounded by a parabola and line. To find the area of a parabolic segment, Archimedes considers a certain inscribed triangle. The base of this triangle is the given chord of the parabola, and the third vertex is the point on the parabola such that the tangent to the parabola at that point is parallel to the chord. Proposition 1 of the work states that a line from the third vertex drawn parallel to the axis divides the chord into equal segments. The main theorem claims that the area of the parabolic segment is [math]\displaystyle{ \tfrac43 }[/math] that of the inscribed triangle.

Structure of the text

Archimedes' first proof of the area of a parabolic segment.

Conic sections such as the parabola were already well known in Archimedes' time thanks to Menaechmus a century earlier. However, before the advent of the differential and integral calculus, there were no easy means to find the area of a conic section. Archimedes provides the first attested solution to this problem by focusing specifically on the area bounded by a parabola and a chord.

Archimedes gives two proofs of the main theorem: one using abstract mechanics and the other one by pure geometry. In the first proof, Archimedes considers a lever in equilibrium under the action of gravity, with weighted segments of a parabola and a triangle suspended along the arms of a lever at specific distances from the fulcrum. When the center of gravity of the triangle is known, the equilibrium of the lever yields the area of the parabola in terms of the area of the triangle which has the same base and equal height. Archimedes here deviates from the procedure found in On the Equilibrium of Planes in that he has the centers of gravity at a level below that of the balance. The second and more famous proof uses pure geometry, particularly the sum of a geometric series.

Of the twenty-four propositions, the first three are quoted without proof from Euclid's Elements of Conics (a lost work by Euclid on conic sections). Propositions 4 and 5 establish elementary properties of the parabola. Propositions 6–17 give the mechanical proof of the main theorem; propositions 18–24 present the geometric proof.

Geometric proof

Archimedes' second proof dissects the area using an arbitrary number of triangles.

Dissection of the parabolic segment

The main idea of the proof is the dissection of the parabolic segment into infinitely many triangles, as shown in the figure to the right. Each of these triangles is inscribed in its own parabolic segment in the same way that the blue triangle is inscribed in the large segment.

Areas of the triangles

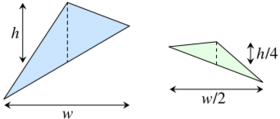
In propositions eighteen through twenty-one, Archimedes proves that the area of each green triangle is [math]\displaystyle{ \tfrac18 }[/math] the area of the blue triangle, so that both green triangles together sum to [math]\displaystyle{ \tfrac14 }[/math] the area of the blue triangle. From a modern point of view, this is because the green triangle has [math]\displaystyle{ \tfrac12 }[/math] the width and [math]\displaystyle{ \tfrac14 }[/math] the height of the blue triangle:

Following the same argument, each of the [math]\displaystyle{ 4 }[/math] yellow triangles has [math]\displaystyle{ \tfrac18 }[/math] the area of a green triangle or [math]\displaystyle{ \tfrac1{64} }[/math] the area of the blue triangle, summing to [math]\displaystyle{ \tfrac4{64} = \tfrac1{16} }[/math] the area of the blue triangle; each of the [math]\displaystyle{ 2^3 = 8 }[/math] red triangles has [math]\displaystyle{ \tfrac18 }[/math] the area of a yellow triangle, summing to [math]\displaystyle{ \tfrac{2^3}{8^3} = \tfrac1{64} }[/math] the area of the blue triangle; etc. Using the method of exhaustion, it follows that the total area of the parabolic segment is given by

[math]\displaystyle{ \text{Area}\;=\;T \,+\, \frac14T \,+\, \frac1{4^2}T \,+\, \frac1{4^3}T \,+\, \cdots. }[/math]

Here T represents the area of the large blue triangle, the second term represents the total area of the two green triangles, the third term represents the total area of the four yellow triangles, and so forth. This simplifies to give

[math]\displaystyle{ \text{Area}\;=\;\left(1 \,+\, \frac{1}{4} \,+\, \frac{1}{16} \,+\, \frac{1}{64} \,+\, \cdots\right)T. }[/math]

Sum of the series

Archimedes' proof that 1/4 + 1/16 + 1/64 + ⋯ = 1/3

To complete the proof, Archimedes shows that

[math]\displaystyle{ 1 \,+\, \frac{1}{4} \,+\, \frac{1}{16} \,+\, \frac{1}{64} \,+\, \cdots\;=\; \frac{4}{3}. }[/math]

The formula above is a geometric series—each successive term is one fourth of the previous term. In modern mathematics, that formula is a special case of the sum formula for a geometric series.

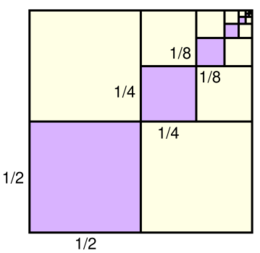
Archimedes evaluates the sum using an entirely geometric method, illustrated in the adjacent picture. This picture shows a unit square which has been dissected into an infinity of smaller squares. Each successive purple square has one fourth the area of the previous square, with the total purple area being the sum

[math]\displaystyle{ \frac{1}{4} \,+\, \frac{1}{16} \,+\, \frac{1}{64} \,+\, \cdots. }[/math]

However, the purple squares are congruent to either set of yellow squares, and so cover [math]\displaystyle{ \tfrac13 }[/math] of the area of the unit square. It follows that the series above sums to [math]\displaystyle{ \tfrac43 }[/math] (since [math]\displaystyle{ 1 + \tfrac13 = \tfrac43 }[/math]).

See also

• Quadrature (geometry)
• History of calculus

Further reading

• Ajose, Sunday and Roger Nelsen (June 1994). "Proof without Words: Geometric Series". Mathematics Magazine 67 (3): 230. doi:10.2307/2690617. 
• Ancora, Luciano (2014). "Quadrature of the parabola with the square pyramidal number". Archimede 66 (3). https://www.zentralblatt-math.org/matheduc/en/?q=an%3A2016f.01058. 
• Bressoud, David M. (2006). A Radical Approach to Real Analysis (2nd ed.). Mathematical Association of America. ISBN 0-88385-747-2. .
• Dijksterhuis, E.J. (1987) "Archimedes", Princeton U. Press ISBN 0-691-08421-1
• Edwards Jr., C. H. (1994). The Historical Development of the Calculus (3rd ed.). Springer. ISBN 0-387-94313-7. .
• Heath, Thomas L. (2011). The Works of Archimedes (2nd ed.). CreateSpace. ISBN 978-1-4637-4473-1. 
• Simmons, George F. (2007). Calculus Gems. Mathematical Association of America. ISBN 978-0-88385-561-4. https://archive.org/details/calculusgemsbrie0000simm. .
• Stein, Sherman K. (1999). Archimedes: What Did He Do Besides Cry Eureka?. Mathematical Association of America. ISBN 0-88385-718-9. https://archive.org/details/archimedeswhatdi00stei. 
• Stillwell, John (2004). Mathematics and its History (2nd ed.). Springer. ISBN 0-387-95336-1. .
• Swain, Gordon and Thomas Dence (April 1998). "Archimedes' Quadrature of the Parabola Revisited". Mathematics Magazine 71 (2): 123–30. doi:10.2307/2691014. 
• Wilson, Alistair Macintosh (1995). The Infinite in the Finite. Oxford University Press. ISBN 0-19-853950-9. .

External links

• Casselman, Bill. "Archimedes' quadrature of the parabola". http://www.math.ubc.ca/~cass/archimedes/parabola.html.  Full text, as translated by T.L. Heath.
• Xavier University Department of Mathematics and Computer Science. "Archimedes of Syracuse". Archived from the original on 2016-01-13. https://web.archive.org/web/20160113100044/http://www.cs.xu.edu/math/math147/02f/archimedes/archpartext.html. . Text of propositions 1–3 and 20–24, with commentary.
• http://planetmath.org/ArchimedesCalculus