Astronomy:On the Sizes and Distances (Aristarchus)

Short description: Work by Aristarchus of Samos, Greek astronomer

Aristarchus's 3rd century BCE calculations on the relative sizes of, from left, the Sun, Earth and Moon, from a 10th-century CE Greek copy

On the Sizes and Distances (of the Sun and Moon) (Ancient Greek:) is widely accepted as the only extant work written by Aristarchus of Samos, an ancient Greek astronomer who lived circa 310–230 BCE. This work calculates the sizes of the Sun and Moon, as well as their distances from the Earth in terms of Earth's radius.

The book was presumably preserved by students of Pappus of Alexandria's course in mathematics, although there is no evidence of this. The editio princeps was published by John Wallis in 1688, using several medieval manuscripts compiled by Sir Henry Savile. The earliest Latin translation was made by Giorgio Valla in 1488. There is also a 1572 Latin translation and commentary by Frederico Commandino.

Symbols

The work's method relied on several observations:

• The apparent size of the Sun and the Moon in the sky.
• The size of the Earth's shadow in relation to the Moon during a lunar eclipse
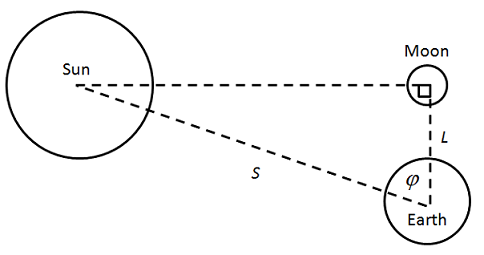
• The angle between the Sun and Moon during a half moon is 90°.

The rest of the article details a reconstruction of Aristarchus' method and results. The reconstruction uses the following variables:

Symbol	Meaning
φ	Angle between the Moon and the Sun during a half moon (directly measurable)
L	Distance from the Earth to the Moon
S	Distance from the Earth to the Sun
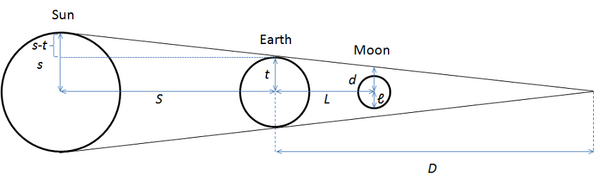
ℓ	Radius of the Moon
s	Radius of the Sun
t	Radius of the Earth
D	Distance from the center of Earth to the vertex of Earth's shadow cone
d	Radius of the Earth's shadow at the location of the Moon
n	Ratio, d/ℓ (a directly observable quantity during a lunar eclipse)
x	Ratio, S/L = s/ℓ (which is calculated from φ)

Half Moon

Aristarchus began with the premise that, during a half moon, the moon forms a right triangle with the Sun and Earth. By observing the angle between the Sun and Moon, φ, the ratio of the distances to the Sun and Moon could be deduced using a form of trigonometry.

From the diagram and trigonometry, we can calculate that

[math]\displaystyle{ \frac{S}{L} = \frac{1}{\cos \varphi} = \sec \varphi. }[/math]

The diagram is greatly exaggerated, because in reality, S = 390 L, and φ is extremely close to 90°. Aristarchus determined φ to be a thirtieth of a quadrant (in modern terms, 3°) less than a right angle: in current terminology, 87°. Trigonometric functions had not yet been invented, but using geometrical analysis in the style of Euclid, Aristarchus determined that

[math]\displaystyle{ 18 \lt \frac{S}{L} \lt 20. }[/math]

In other words, the distance to the Sun was somewhere between 18 and 20 times greater than the distance to the Moon. This value (or values close to it) was accepted by astronomers for the next two thousand years, until the invention of the telescope permitted a more precise estimate of solar parallax.

Aristarchus also reasoned that as the angular size of the Sun and the Moon were the same, but the distance to the Sun was between 18 and 20 times further than the Moon, the Sun must therefore be 18–20 times larger.

Lunar eclipse

Aristarchus then used another construction based on a lunar eclipse:

By similarity of the triangles, [math]\displaystyle{ \frac{D}{L} = \frac{t}{t-d} \quad }[/math] and [math]\displaystyle{ \quad \frac{D}{S} = \frac{t}{s-t}. }[/math]

Dividing these two equations and using the observation that the Sun and Moon appear the same size to people on Earth, [math]\displaystyle{ s/S = \ell/L }[/math], yields

[math]\displaystyle{ \frac{\ell}{s} = \frac{t-d}{s-t} \ \ \implies \ \ \frac{s-t}{s} = \frac{t-d}{\ell} \ \ \implies \ \ \frac{t}{\ell} + \frac{t}{s} = 1 + \frac{d}{\ell}. }[/math]

The rightmost equation can either be solved for [math]\displaystyle{ \ell/t }[/math] or [math]\displaystyle{ s/t }[/math]

[math]\displaystyle{ \frac{\ell}{t} = \frac{1+\dfrac{\ell}{s}}{1 + \dfrac{d}{\ell}},\qquad \frac{s}{t} = \frac{1+\dfrac{s}{\ell}}{1 + \dfrac{d}{\ell}}. }[/math]

These equations can be made to appear simpler by expressing the lengths [math]\displaystyle{ d }[/math] and [math]\displaystyle{ s }[/math] in terms of the moon's radius [math]\displaystyle{ \ell }[/math] as a unit, defining [math]\displaystyle{ \hat{d} = d/\ell }[/math] and [math]\displaystyle{ \hat{s} = s/\ell. }[/math] Then

[math]\displaystyle{ \frac{\ell}{t} = \frac{1+\hat{s}}{\hat{s}(1+\hat{d})},\qquad \frac{s}{t} = \frac{1+\hat{s}}{1+\hat{d}} }[/math]

The above equations give the radii of the Moon and Sun entirely in terms of observable quantities.

The following formulae give the distances to the Sun and Moon in terrestrial units:

[math]\displaystyle{ \frac{L}{t} = \left( \frac{\ell}{t} \right) \left( \frac{180}{\pi \theta} \right) }[/math]

[math]\displaystyle{ \frac{S}{t} = \biggl( \frac{s}{t} \biggr) \left( \frac{180}{\pi \theta} \right) }[/math]

where θ is the apparent radius of the Moon and Sun measured in degrees.

It is unlikely that Aristarchus used these exact formulae, yet these formulae are likely a good approximation for those of Aristarchus.

Results

The above formulae can be used to reconstruct the results of Aristarchus. The following table shows the results of a long-standing (but dubious) reconstruction using n = 2, x = 19.1 (φ = 87°) and θ = 1°, alongside the modern day accepted values.

Quantity	Relation	Reconstruction	Modern
s/t	Sun's radius in Earth radii	6.7	109
t/ℓ	Earth's radius in Moon radii	2.85	3.67
L/t	Earth-Moon distance in Earth radii	20	60.34
S/t	Earth-Sun distance in Earth radii	380	23,481 The error in this calculation comes primarily from the poor values for x and θ. The poor value for θ is especially surprising, since Archimedes writes that Aristarchus was the first to determine that the Sun and Moon had an apparent diameter of half a degree. This would give a value of θ = 0.25, and a corresponding distance to the Moon of 80 Earth radii, a much better estimate. The disagreement of the work with Archimedes seems to be due to its taking an Aristarchus statement that the lunisolar diameter is 1/15 of a "meros" of the zodiac to mean 1/15 of a zodiacal sign (30°), unaware that the Greek word "meros" meant either "portion" or 7°1/2; and 1/15 of the latter amount is 1°/2, in agreement with Archimedes' testimony. A similar procedure was later used by Hipparchus, who estimated the mean distance to the Moon as 67 Earth radii, and Ptolemy, who took 59 Earth radii for this value. Illustrations Some interactive illustrations of the propositions in On Sizes can be found here: Hypothesis 4 states that when the Moon appears to us halved, its distance from the Sun is then less than a quadrant by one-thirtieth of a quadrant [that is, it is less than 90° by 1/30th of 90° or 3°, and is therefore equal to 87°] (Heath 1913:353). Proposition 1 states that two equal spheres are comprehended by one and the same cylinder, and two unequal spheres by one and the same cone which has its vertex in the direction of the lesser sphere; and the straight line drawn through the centres of the spheres is at right angles to each of the circles in which the surface of the cylinder, or of the cone, touches the spheres (Heath 1913:354). Proposition 2 states that if a sphere be illuminated by a sphere greater than itself, the illuminated portion of the former sphere will be greater than a hemisphere (Heath 1913:358). Proposition 3 states that the circle in the Moon which divides the dark and the bright portions is least when the cone comprehending both the Sun and the Moon has its vertex at our eye (Heath 1913:362). Proposition 4 states that the circle which divides the dark and the bright portions in the Moon is not perceptibly different from a great circle in the Moon (Heath 1913:365). Proposition 6 states that the Moon moves [in an orbit] lower than [that of] the Sun, and, when it is halved, is distant less than a quadrant from the Sun (Heath 1913:372). Proposition 7 states that the distance of the Sun from the Earth is greater than 18 times, but less than 20 times, the distance of the Moon from the Earth (Heath 1913:377). In other words, the Sun is 18 to 20 times farther away and wider than the Moon. Proposition 13 states that the straight line subtending the portion intercepted within the earth's shadow of the circumference of the circle in which the extremities of the diameter of the circle dividing the dark and the bright portions in the Moon move is less than double of the diameter of the Moon, but has to it a ratio greater than that which 88 has to 45; and it is less than 1/9th part of the diameter of the Sun, but has to it a ratio greater than that which 21 has to 225. But it has to the straight line drawn from the centre of the Sun at right angles to the axis and meeting the sides of the cone a ratio greater than that which 979 has to 10 125 (Heath 1913:394). Proposition 14 states that the straight line joined from the centre of the Earth to the centre of the Moon has to the straight line cut off from the axis towards the centre of the Moon by the straight line subtending the [circumference] within the Earth's shadow a ratio greater than that which 675 has to 1 (Heath 1913:400). Proposition 15 states that the diameter of the Sun has to the diameter of the Earth a ratio greater than 19/3, but less than 43/6 (Heath 1913:403). This means that the Sun is (a mean of) ​6 3⁄4 times wider than the Earth, or that the Sun is ​13 1⁄2 Earth-radii wide. The Moon and Sun must then be ​20 1⁄4 and 387 Earth-radii away from us in order to subtend an angular size of 2º. Proposition 17a in al-Tusi's medieval Arabic version of the book On Sizes states that the ratio of the distance of the vertex of the shadow cone from the center of the Moon (when the Moon is on the axis [that is, at the middle of an eclipse] of the cone containing the Earth and the Sun) to the distance of the center of the Moon from the center of the Earth is greater than the ratio 71 to 37 and less than the ratio 3 to one (Berggren & Sidoli 2007:218). In other words, that the tip of the Earth's shadow cone is between 108/37 and four times farther away than the Moon. Known copies Library of Congress Vatican Exhibit. See also Aristarchus of Samos Eratosthenes (c. 276 – c. 194/195 BC), a Greek mathematician who calculated the circumference of the Earth and also the distance from the Earth to the Sun. Hipparchus (c. 190 – c. 120 BC), a Greek mathematician who measured the radii of the Sun and the Moon as well as their distances from the Earth. On the Sizes and Distances (Hipparchus) Posidonius (c. 135 – c. 51 BC), a Greek astronomer and mathematician who calculated the circumference of the Earth. Notes Bibliography Gomez, Alberto (2023). Decoding Aristarchus. Berlin: Peter Lang Verlag. ISBN 9783631892619. https://www.peterlang.com/document/1288830.  Heath, Thomas (1913). Aristarchus of Samos, the Ancient Copernicus. Oxford: Clarendon. https://archive.org/details/aristarchusofsam00heat.  This was later reprinted, see (ISBN:0-486-43886-4). van Helden, A. Measuring the Universe: Cosmic Dimensions from Aristarchus to Halley. Chicago: Univ. of Chicago Pr., 1985. ISBN:0-226-84882-5.