Condorcet's jury theorem

Short description: Political science theorem

Graph of cumulative probabilities of success (y axis) for a few binomial distributions with given individual chance of success (x axis) and number of “jurors” (color).

Condorcet's jury theorem is a political science theorem about the relative probability of a given group of individuals arriving at a correct decision. The theorem was first expressed by the Marquis de Condorcet in his 1785 work Essay on the Application of Analysis to the Probability of Majority Decisions.

Proof 1: Calculating the probability that two additional voters change the outcome

To avoid the need for a tie-breaking rule, we assume n is odd. Essentially the same argument works for even n if ties are broken by adding a single voter.

Now suppose we start with n voters, and let m of these voters vote correctly.

Consider what happens when we add two more voters (to keep the total number odd). The majority vote changes in only two cases:

• m was one vote too small to get a majority of the n votes, but both new voters voted correctly.
• m was just equal to a majority of the n votes, but both new voters voted incorrectly.

The rest of the time, either the new votes cancel out, only increase the gap, or don't make enough of a difference. So we only care what happens when a single vote (among the first n) separates a correct from an incorrect majority.

Restricting our attention to this case, we can imagine that the first n-1 votes cancel out and that the deciding vote is cast by the n-th voter. In this case the probability of getting a correct majority is just p. Now suppose we send in the two extra voters. The probability that they change an incorrect majority to a correct majority is (1-p)p², while the probability that they change a correct majority to an incorrect majority is p(1-p)(1-p). The first of these probabilities is greater than the second if and only if p > 1/2, proving the theorem.

Proof 2: Calculating the probability that the decision is correct

This proof is direct; it just sums up the probabilities of the majorities. Each term of the sum multiplies the number of combinations of a majority by the probability of that majority. Each majority is counted using a combination, n items taken k at a time, where n is the jury size, and k is the size of the majority. Probabilities range from 0 (= the vote is always wrong) to 1 (= always right). Each person decides independently, so the probabilities of their decisions multiply. The probability of each correct decision is p. The probability of an incorrect decision, q, is the opposite of p, i.e. 1 − p. The power notation, i.e. [math]\displaystyle{ p^x }[/math] is a shorthand for x multiplications of p.

Committee or jury accuracies can be easily estimated by using this approach in computer spreadsheets or programs.

As an example, let us take the simplest case of n = 3, p = 0.8. We need to show that 3 people have higher than 0.8 chance of being right. Indeed:

0.8 × 0.8 × 0.8 + 0.8 × 0.8 × 0.2 + 0.8 × 0.2 × 0.8 + 0.2 × 0.8 × 0.8 = 0.896.

Asymptotics

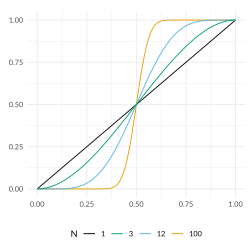
The probability of a correct majority decision P(n, p), when the individual probability p is close to 1/2 grows linearly in terms of p − 1/2. For n voters each one having probability p of deciding correctly and for odd n (where there are no possible ties):

[math]\displaystyle{ P(n, p) = 1/2 + c_1 (p - 1/2) + c_3 (p - 1/2)^3 + O\left( (p - 1/2)^5 \right), }[/math]

where

[math]\displaystyle{ c_1 = {n \choose {\lfloor n/2 \rfloor}} \frac{\lfloor n/2 \rfloor + 1}{4^{\lfloor n/2 \rfloor}} = \sqrt{\frac{2n + 1}{\pi}} \left(1 + \frac{1}{16n^2} + O(n^{-3})\right), }[/math]

and the asymptotic approximation in terms of n is very accurate. The expansion is only in odd powers and [math]\displaystyle{ c_3 \lt 0 }[/math]. In simple terms, this says that when the decision is difficult (p close to 1/2), the gain by having n voters grows proportionally to [math]\displaystyle{ \sqrt{n} }[/math].

The theorem in other disciplines

The Condorcet jury theorem has recently been used to conceptualize score integration when several physician readers (radiologists, endoscopists, etc.) independently evaluate images for disease activity. This task arises in central reading performed during clinical trials and has similarities to voting. According to the authors, the application of the theorem can translate individual reader scores into a final score in a fashion that is both mathematically sound (by avoiding averaging of ordinal data), mathematically tractable for further analysis, and in a manner that is consistent with the scoring task at hand (based on decisions about the presence or absence of features, a subjective classification task)

The Condorcet jury theorem is also used in ensemble learning in the field of machine learning. An ensemble method combines the predictions of many individual classifiers by majority voting. Assuming that each of the individual classifiers predict with slightly greater than 50% accuracy and their predictions are independent, then the ensemble of their predictions will be far greater than their individual predictive scores.

Applicability to democratic processes

Many political theorists and philosophers use the Condorcet’s Jury Theorem (CJT) to defend democracy, see Brennan and references therein. Nevertheless, it is an empirical question whether the theorem holds in real life or not. Note that the CJT is a double-edged sword: it can either prove that majority rule is an (almost) perfect mechanism to aggregate information, when [math]\displaystyle{ p\gt 1/2 }[/math], or an (almost) perfect disaster, when [math]\displaystyle{ p\lt 1/2 }[/math]. A disaster would mean that the wrong option is chosen systematically. Some authors have argued that we are in the latter scenario. For instance, Bryan Caplan has extensively argued that voters' knowledge is systematically biased toward (probably) wrong options. In the CJT setup, this could be interpreted as evidence for [math]\displaystyle{ p\lt 1/2 }[/math].

Recently, another approach to study the applicability of the CJT was taken. Instead of considering the homogeneous case, each voter is allowed to have a probability [math]\displaystyle{ p_i\in[0,1] }[/math], possibly different from other voters. This case was previously studied by Daniel Berend and Jacob Paroush and includes the classical theorem of Condorcet (when [math]\displaystyle{ p_i=p~~ \forall~i\in\mathbb{N} }[/math]) and other results, like the Miracle of Aggregation (when [math]\displaystyle{ p_i=1/2 }[/math] for most voters and [math]\displaystyle{ p_i=1 }[/math] for a small proportion of them). Then, following a Bayesian approach, the prior probability (in this case, a priori) of the thesis predicted by the theorem is estimated. That is, if we choose an arbitrary sequence of voters (i.e., a sequence [math]\displaystyle{ (p_i)_{i\in\mathbb{N}} }[/math] ), will the thesis of the CJT hold? The answer is no. More precisely, if a random sequence of [math]\displaystyle{ p_i }[/math] is taken following an unbiased distribution that does not favor competence, [math]\displaystyle{ p_i\gt 1/2 }[/math], or incompetence, [math]\displaystyle{ p_i\lt 1/2 }[/math], then the thesis predicted by the theorem will not hold almost surely. With this new approach, proponents of the CJT should present strong evidence of competence, to overcome the low prior probability. That is, it is not only the case that there is evidence against competence (posterior probability), but also that we cannot expect the CJT to hold in the absence of any evidence (prior probability).

Further reading

• Condorcet method
• Condorcet paradox
• Jury theorem
• Wisdom of the crowd