Biology:Physical oncology
Physical oncology (PO) is defined as the study of the role of mechanical signals in a cancerous tumor. The mechanical signals can be forces, pressures ("pull", "push" and "shear" designating the forces / pressures that push, pull or are tangential). If we generalize we will speak of "stress field" and "stress tensor".[1][2][3] A cancerous tumor (or "solid tumor" in the jargon of oncologists to differentiate them from hematological malignancies) is an organ consisting of two tissues: in the center the cancerous tumor proper and around the ExtraCellular Matrix (ECM), sometimes called stroma, chorion or connective tissue. The concept of connective tissue is interesting because it defines a tissue that travels the entire organism (except the brain) and is a preferred transmitter of mechanical signals. But for the cancer organ - isolated from this connective system - we prefer the term ECM.
The cancerous tissue is derived from a normal tissue of the body: breast cancer arises from a cancerous transformation of the normal mammary glandular tissue. It looks more or less like the original tissue: it is said that it is more or less differentiated; poorly differentiated it has a microscopic appearance that is far from normal tissue and is then "poorly prognostic", will make more metastases and will be more difficult to treat.
We are only considering cancers derived from "epithelia", that is to say the tissue that covers the organs in their interfaces with air, liquids ... or the outside world. Epithelial cells are contiguous and polarized. More than 90% of cancers (breast, prostate, colon / rectum, bronchi, pancreas, etc.) arise from these epithelia after a long process of cancerization.
Both tissues of the cancer organ
The ECM
ECM is a mixture of cells (immune, fibroblasts, etc.) dispersed in proteins, most of them collagen. It surrounds the tumor.
It is analogous to connective tissue and basal membrane, which is a local condensation, located below normal epithelia. This connective tissue allows oxygen and nutrients to diffuse to the epithelia, which are not vascularized.
In the tumor ECM, rapidly, beyond one mm3 of tumor is formed a network of blood vessels, the "neovascularization" (induced by "neoangiogenesis") around the tumor and which will allow the diffusion of oxygen and nutrients in the cancer tissue itself, which is not vascularized.[4]
The cancerous tissue
The cancerous tissue itself, derived from the cancerous transformation of an epithelium.
Cancerization
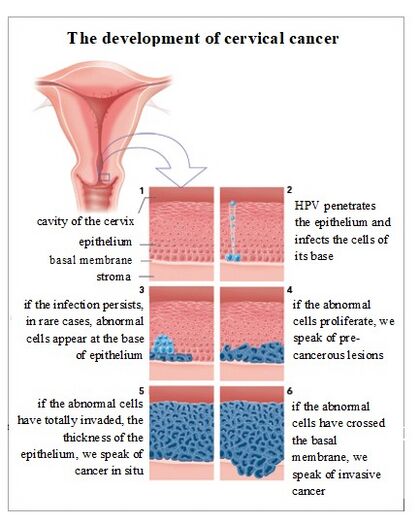
It's a multi-year process. The appearance of cancer is signified by the crossing of the basement membrane to the underlying connective tissue by one or more cancer cells.
The rediscovery of the importance of mechanical signals in biology of living organisms
Several teams, in the USA in particular, had maintained an expertise in the study of non-biological signals in oncology (Donald Ingber, Mina Bissell then Valerie Weaver, Rakesh J Jain among others).[5][6][7]
But the absolute dominance of genetics and molecular biology since the middle of the 20th century had marginalized this approach until its revival at the beginning of the 21st century. This renewal takes into account the immense gains of genetics and molecular biology in the mechanobiological approach. On the other hand, the PO validates results thanks to these achievements but does not use the concepts.
To properly locate the PO and the mechanical signals
Biology / Mechanics comparison
| Input Signal | Output Signal | |
| Biology | Biological | Biological |
| Mechanobiology | Mechanical | Biological |
| Physical Oncology | Mechanical | Mechanical |
Some differences between biological and physical signals
| Support | Transmission of the signal | Modulation of the signal | Nature of the Signal | Action | Reversibility in space | |
| Biological | Liquid | Slow | Difficult | Biochemical | Slow | No |
| Incompressible | Step by step | Unidirectional | ||||
| Physical | Semisolid
(20% of cell volume) Compressible |
Fast
Almost instantaneous |
Easy | Mechanical | Fast | Yes
Bidirectional |
The use of mechanical signals is therefore also the support of mechanobiology whose objective is very different from the PO. Indeed, as shown in the table above, the study of mechanotransduction, which is the support of mechanobiology, uses a mechanical "input" (signal input) but the signal collected at the output (the "output") is biological. As a result, many of the articles published in mechanobiology end with the phrase "we have defined a target to find a therapeutic molecule", which precludes any therapeutic approach by the mechanical signals themselves.
But this shift from the physical sciences to the biological sciences is problematic, in the absence of any bridge between these two sciences, one quantitative, physics based on mathematical language and the other qualitative, based on the laws of genetics and molecular biology.
OP aims to study the effect of a mechanical input on a mechanical output. We will see that this output can be synthesized in tissue architecture.
Definition of the tissue phenotype
The diagnosis of cancer is made by looking under the microscope a fragment of the tumor (biopsy). The tissue phenotype - here cancerous tissue - is the sum of the cellular and tissue phenotype. The phenotype of the cell is supposed to be the translation of the genotype (and of the environment: epigenetics) expressed in a given cell: thus, a liver cell does not look like a pancreas cell at all because it does not express the same genes (yet all present in the genome of all cells).
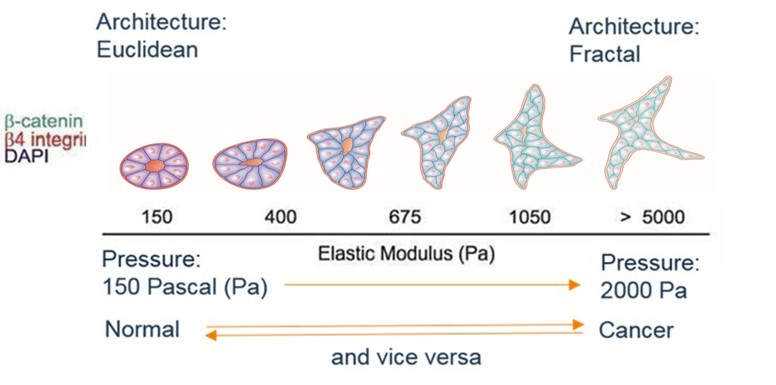
These characteristics are summarized by: differentiation, cell division (mitosis), apoptosis (or "cell suicide") and cell death. The doctor in charge of the diagnosis under the microscope (the pathologist) will describe the biopsy based on these criteria. The tissue phenotype is centered on architecture: the normal tissue is Euclidean (hexagons, trapezes, circles ...) familiar to our brains; the cancerous is fractal, less familiar. It can be summed up in a coefficient of fractality very strongly correlated with the prognosis and the components of the cellular phenotype. Thus, a high coefficient of fractality is correlated with a poorly differentiated tumor, with many mitoses, little apoptosis and a poor prognosis.
And here we have to mention Mina Bissell: "in oncology the tissue phenotype is dominant over the cellular genotype".[6][8]
The quiet revolution: three-dimensional models (3D) and other models (spheroids, animal xenograft ...)
OP was made possible by apparently minor technical changes that allowed in vitro and then in vivo models to be closer to the reality of the cancerous tumor in the patient.
For a very long time, two-dimensional (2D) cell cultures have been used in glass and then plastic boxes. The cultured cells thus adhered to the bottom, in very rigid material, rigidity measured by the Young's modulus, very high for these supports.
Young's module
The Young modulus or modulus of elasticity is the constant that relates the tensile / compressive stress and the beginning of the deformation of an isotropic elastic material.
It is expressed in Pascal (Pa), unit of pressure.
Then appeared the three-dimensional (3D) cultures with cells which constituted multicellular spheres by dividing and were surrounded by a gel-like culture medium at the Young's modulus close to those of the living and variable tissues, for example depending on the amount of collagen surrounding these cultures in 3D. Organoids, spheroids are variants of this type of culture.[9]
At the same time the animal models evolved there also towards more similarity with the clinical reality. The human tumor xenograft is today the standard and the orthotopic transplant - for example human cancer of the pancreas in the mouse pancreas - is one of the best experimental models.[10]
The link between the clinic and the experiment becomes more realistic since these 3D cultures make it possible to use the culture medium surrounding the growing tumor tissue as a "virtual ECM", which can be varied, for example, to increase the pressure around the tumor grown.
Similarly, xenograft can constitute a cancer organ with both tissues even if the ECM is of animal origin.
What is hard in cancer
It's the ECM. So, when a doctor or a patient feels "a hard lump in the breast" and it is a cancer, what is hard is the ECM while the tumor itself is softer than the normal breast tissue. This has been demonstrated in vitro and more recently ex vivo and will soon be in vivo.[citation needed]
In vitro
The role of stress on the growth of a spheroid in vitro had already been shown (G Helminger already cited), but the experiment of Matthew Paszek (last signatory of the article: Valerie Weaver) in 2005 will give a new dimension to this use of mechanical signals in vitro by showing the passage from a normal architecture of a breast acinus - the elementary unit of the mammary gland - to a cancerous architecture under the influence of a single variable, mechanical, here the surface tension caused by an increasing concentration of collagen in the culture medium surrounding the tumor.
We clearly see the transition from one architecture to another, progressive and reversible if the constraint is relaxed. Changes in the concentration of biological markers of cancerization (catenins, integrins, etc.), with the disappearance of the central cavity, highlight the shift in tissue phenotype.
In addition, this experiment opens the way to the reversibility of cancer, the royal way of treatment, which is intended to replace conventional destructive approaches.
Another experiment is equally spectacular:
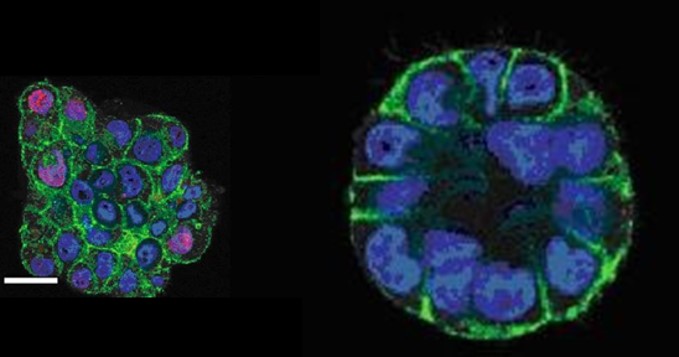
According to Gautham Venugopalan ASCB 2012
Malignant breast cells cultured in vitro in 3D form a "disorganized" mass (translate fractal) on the left in the photo.
But after a few minutes of compression, they form an acinus, Euclidean, on the right.
Other authors have extended this work on different models with different mechanical signals. F Montel et al., in particular, has demonstrated on spheroids of human cancer origin the very significant increase in apoptosis in the response to stress.
These 3D cultures have also shown the organization of collagen fibers within the ECM and beyond, allowing remote transmission of mechanical signals and a 'tensor dialogue' between the tumor, ECM and normal environment.[11][12][13][14][15]
But these experiments have in common to apply physical variables (surface tension, osmotic pressure ...) that cannot be used in vivo.
Ex vivo
M Plodinec et al. extended this work using breast cancer biopsies kept alive ex vivo and then passed to an Atomic Force Microscope (AFM) to measure the Young's moduli of the different tissue components of these normal breast biopsies, tumors benign and malignant.
This team finds the results already widely explored on isolated cells and 2D cultures: the cancerous tissues have a Young's modulus around 0.8 kPa, normal tissues have a modulus around 1.1 kPa. The ECM has a module greater than 2 kPa.
This difference - the cancerous tissue is softer than its normal counterpart - crosses all oncology, all cancers combined and from the dysplastic cell to the tumor and metastatic cells.[16][17][18][19][20]
All measurements, cell and tissue, converge towards the same conclusion: the modulus of the cancerous tissue is inversely correlated with the 'dangerousness' of the cancer: the softer the tumor, the more it is undifferentiated, the more it will give metastases, the less it will respond to current treatments...
In vivo
In OP for therapeutic purposes, we find only the article by R Brossel et al. (2016)[21] which shows the possibility of acting on a tumor grafted subcutaneously in the rodent by applying a constraint.
It is validated in this Proof of Concept. There is a significant difference between the treated group and the control groups. This difference concerns the volume of the tumor measured in vivo which is very significantly decreased (p = 0.015) in the treated group compared to the 3 control groups (with particles and without gradient, with gradient and without particles, without gradient or particles). There is also a significant difference in favor of the treated group when measuring the surface of the living tumor, ex vivo, on digitized histological sections (p = 0.001).
Results
| Groups of grafted mice | Median Tumor Volume (mm3) | p (Significance of the difference) |
| Groups treated | 529 | p = 0.015 |
| Control groups* | 1 334 | |
| Mean
(mm2) |
Tumor area on histological sections digitized ex vivo | |
| Treated Group | 7.7 | p = 0.001 |
| Control Groups * | 23.1 ; 21.4 ; 26.8 |
* Three groups of mice: with particles only; with gradient alone; without particles or gradient
This field imposed on the ECM is superimposed on that already present in the tumor tissue. Note the difference with in vitro: there is no confinement by the ECM in vitro or anchoring by the integrins which ensure the physical continuity between the ECM and the tumor tissue and thus allow the propagation to distance of mechanical signals.
In this perspective the "field of stress" becomes the therapeutic agent.
This stress is exerted via ferric nanoparticles, therefore magnetizable, located around the tumor (and not in the tumor) and subjected from outside the animal to a magnetic field gradient generated by fixed magnets. The nanoparticles then act as '‘BioActuators’ transforming part of the magnetic energy into mechanical energy.
To this work we can link the European project "Imaging Force of Cancer" which as its name indicates aims to measure, voxel by voxel, the constraints involved within the tumoral tissue. This program focuses on the breast, the primitive liver and the brain.
This project is based on MRI elastography, which is the reference method for in vivo, in situ and non-perturbative measurement of the strain, that is to say the very small elastic strain caused in the tissue will give access to the measure of "stress" that is to say of the constraint. It should therefore make it possible to construct the stress tensor of the tumor tissue in vivo, in situ, without significant disturbance intra-tumoral, obligatory starting base to hope to modify it.[22][23][24][25]
There is also an in vivo experiment which demonstrates the increase of the signals coming from the integrins, induced by the increase of the rigidity of the matrix[26]
The isolated cell
Micropatterning
The cellular patterning allowed to show the dependence of the cellular architecture on the tensions generated by the support, variable according to the rigidity of these supports. This made it possible to hypothesize about the transmission of mechanical signals between the "outside", here the support (glass then plastic then gel), and the CytoSKeleton (CSK) and the nucleus.
The equilibrium, in the CSK of each cell, is between contractile microfilaments and microtubules resistant to compression; it is also done in the membership of the ECM by a game of pressure and tension that cancel out in a situation of equilibrium. Energy is given by actin.
Micropatterning has clearly shown these phenomena on the scale of a cell fixed on a support.
Increased stiffness of the ECM: the spreading of the cell - on the support, representation of the ECM - is necessary for the cell division (thus the growth).
Decrease of the rigidity of the ECM: when the ECM is deformed, the cell traction causes the stop of the growth and a differentiation of the cell or an apoptosis.
The soft material that transmits the mechanical signals is therefore pre-stressed and this allows the transmission of forces in the body with a quantitative distribution according to the scale: the skeleton, a macroscopic structure, will transmit much greater forces than an isolated organ.
On the scale of a tissue of an organ, the entire mechanical signal transmission network, including integrins, cadherins, focal adhesions (all intercellular junctions and ETM / cells), membrane, CSK, etc. also support the production of energy. Indeed, mitochondria are an integral part of this network and semi-solid (non-liquid) phase biochemistry is an important part of tissue metabolism.
Here we find a principle of treatment by the mechanical signals.[27][28][29]
The circulating cell
Circulating Tumor Cells (CTCs) are isolable and their rigidity can be measured quite easily. Numerous articles have been able to verify what was already known for cells in 2D culture: the Young's modulus of CTC is very strongly correlated with the severity of cancer in all its parameters: differentiation, metastatic potential, prognostic and predictive correlation...
And these correlations are valid for metaplastic, dysplastic, in situ and cancerous cells.[17]
The journey of the metastatic cell
These CTCs must first cross the ECM, enter the bloodstream or lymphatic vessels, and then leave the circulation to attach to a tissue for metastasis. Many articles have recently commented on this "journey" and the many physical elements that punctuate it.[30][31][32]
The different components of the constraint
The tumor accumulates mechanical energy during its growth. In an article by Stylianopoulos, the author uses a simple technique to highlight tumor constraints: an ex vivo tumor laser cutting frees the accumulated constraints. They are expressed as bulges that can be measured and related to the underlying stress. In the center of the tumor the radial and circumferential stresses are compressive; in the periphery of the tumor the radial stress is compressive, and the circumferential stress is a linear traction along the outer limit of the tumor.[33]
Tumor growth causes stress on the healthy tissues around it.[34]
The ExtraCellular Matrix (ECM) and the cells in contact with the ECM exert mutual tensions.
The cells of the tumor tissue exert tensions between themselves.
This results in a change in fluid flow in the tumor with an increase in intratumoral interstitial pressure.
The internal tension present in the excised tumor can be called "residual stress": when we cut it we clearly see an expansion of the volume which shows this residual tension.[33][35]
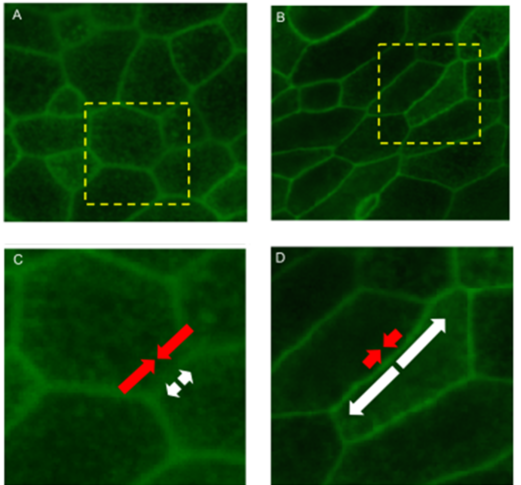
Another track was opened by J Fredberg, in two dimensions:
As the intercellular adhesion stress increases, there is a histological architecture change and a solid to liquid phase transition.
The mechanical energy, cellular cohesion of the tumor tissue, is attributable, in large part, intercellular junctions and can be expressed in linear traction that has two components:
- Contraction energy in red, positive, which comes from the CSK and which minimizes the intercellular surface (Euclidean, pseudo solid when it dominates);
- Energy of adhesion, in white, negative and which maximizes the surface (fractal, pseudo liquid when it dominates).
Soft matter
Popularized by Pierre Gilles de Gennes the term soft matter refers to the study of materials between solid and liquid; at ambient temperature, that of biology, thermal energy (kT) is of the same order of magnitude as the interaction energies between the various components. Due to this entropy / enthalpy balance these biological systems can be organized in a radically different way under the influence of small variations of the outside.
The physics of PO is a soft matter physics.
The stress tensor
This is the generalization of the concept of constraint field. It summarizes in a mathematical expression all the pressures involved in a volume. Here, it is the volume of the tumor with a solid sphere, the tumor tissue, predominantly viscoelastic and a hollow sphere, the ECM, predominantly elastic. The solid sphere is embedded in the hollow sphere.
Organization of CSK and continuity of structures transmitting mechanical signals
The mechanical signals travel through the organs, without any break in continuity. At the tissue level, it is the connective tissue or the ECM that ensures this continuity. At the cellular level, it is the continuity between the connective tissue, the cell membrane, the CSK and the nucleus that ensures this transmission.[36][37]
At what scale? The laws of biology / physics
A hitherto dominant approach is the "bottom up": the understanding of the biological mechanisms (mechanoreceptors, actin and other components of CSK, intracellular signaling, gene effectors, etc.) must lead to an understanding of the phenomena at scale, above be here mesoscopic, tissue.[38]
There are success stories of this approach when one can identify a faulty gene with a mutation and it is possible to act by a drug on the outcome of the mutation: a receptor or an enzyme.
This "one-to-one and first-degree equation" allowed Chronic Myeloid Leukemia to be controlled by imatinib. The defective BCR-ABL gene makes it possible to manufacture an abnormal version of an enzyme of the Tyrosine Kinase type present in leukemic cells. Imatinib inhibits this enzyme and the manufacture of these cells.[39][40]
These few exceptions have led one to believe that this reasoning could be applied to cancers as a whole.
But the "equation" of cancer is much more complex. And the massive failure of "targeted therapies" to cure cancer is the illustration. These targeted therapies have cured only 50% of HER2 positive breast cancers treated with adjuvant therapy after local cancer treatment. That is 3% of breast cancers. That's all. Moreover, their participation in the "chronicization" of the breast and prostate - even some colon or rectum - is very minor compared to chemo / hormonotherapy, much better used today.
The other approach, "top down", takes into account the emergence of unpredictable phenomena through the reductionist approach. Thus, the experimental evidence showing that carcinogenesis is a process bound to emerge a break geometry of the tissue architecture requires abandoning the genetic level or above genetics to get into systems biology and put the matter to cell/tissue level.
In fact, cell phenotypes are emergent phenomena that result from intercellular nonlinear interactions and interaction with the environment that is to say the ECM. This is usually described in a phase space where attractors dot the landscape and are points of stability or instability.[41]
Fractality
The cancer is fractal and this in all its components and at different scales micro/meso and macroscopic.
This geometry is recent and still little integrated in our mental representations.[42]
The first observation was the fractal nature of microcalcifications linked to breast cancer on a mammogram.[43]
Then the fractality of the cancer has been demonstrated on different structures of the organ cancer - neoangiogenesis, tumor growth zone, tumor tissue ... - and at the microscopic scale: cell nucleus, cell surface.[44][45][46]
Synergy
A synergy between immunotherapy and the use of mechanical signals is highly likely as shown by two recent papers that describe the control of PDL-1 expression and immunocompetent cells by extracellular matrix stiffness.[47][48]
Thermodynamics
Fractality is a means that evolution has found to minimize the energy used to distribute resources. Remember that cancer uses a source of energy different from other tissues, less efficient in yield.[49][50][51][52][53]
The death of the patient
What is a cancer patient dying of?
There are several possibilities: the infectious complications related to the immunodepression due to the disease and the treatments, the attack of a vital organ like the lungs invaded by so many metastases that the breathing becomes impossible, the thrombotic complications like a pulmonary embolism, an end of life precipitated by analgesic treatments whose doses are increased. But behind all these causes is the diversion of energy by cancer that behaves like a parasite that kills its host. In some particularly local cancers, such as pancreatic cancer, this is particularly noticeable: the patient dies of cachexia, that is to say of great malnutrition.
The big ancestors and the dust under the carpet
The brilliant intuitions of D'Arcy Thompson are now accepted by all: the shape that organs (including cancer) and organisms take depends on the variations in time and space of the mechanical properties of the tissues. But he describes, without making any assumptions about why and how.
J Wolff described the histological variations of the bone according to the load which weighs on him.
This is well known to thoracic surgeons: a vein removed to bypass a coronary artery and grafted into the artery position changes histology and becomes an artery due to this new pressure regime.[54][55][56]
The same conclusion can be drawn from studies on the transformation of bone and cartilage tissue under different pressure regimes.
Since the 1950s, the genetic paradigm has emerged. Cancers arise from one (or some) mutated cell(s) and progression results from the sequential accumulation of tumor-free random mutations of all homeostatic controls.
The discovery of oncogenes, suppressor genes, stability genes (caretaker) is a coherent and reliable set to track the birth and progression of cancer.
But the contradictory experimental facts are not lacking: the carcinogens are not all mutagens (hormones...); the target of carcinogens may be the ECM and not the cell; an ECM exposed to a carcinogen brought into contact with a non-cancerous tissue will cause cancer of this tissue, but not vice versa; a cancerous tissue in close contact with a normal ECM may become normal tissue again.[57][58]
Other authors have shown that it is possible to return to a normal architecture a cancerous tissue when it was taken in charge by an embryonic environment then by somatic tissue.[59][60][61][62]
These last examples plead for the reality of the possible reversion of the cancerous to the non-cancerous.
Finally, more cancers are due to infectious "causes" than to genetic "causes".
These last examples plead for the reality of the possible reversion of the cancerous to the non-cancerous.
Towards a global approach to cancer
Any theory of carcinogenesis must explain cancerization since its onset, dysplasia, in situ, then crossing of the basement membrane, the growth of the primary tumor and the appearance of metastases.
Let us quote DW Smithers (1962): "cancer is no more a disease of the cells than a traffic jam is a disease of cars".
We therefore see a global approach taking into account both the mechanical and biological signals in this long process that goes from dysplasia to metastases.
This new branch of biology has consequences beyond oncology, in embryology, tissue engineering, etc.[63][64][65][66]
It is only time for Physical Oncology to become visible. Visible because now integrable into an imagery that can measure mechanical signals, and visible in the scientific field as a full component of carcinogenesis.
References
- ↑ Jonietz, Erika (2012-11-21). "Mechanics: The forces of cancer" (in en). Nature 491 (7425): S56–S57. doi:10.1038/491s56a. PMID 23320288.
- ↑ "The Forces of Cancer". http://www.the-scientist.com/?articles.view/articleNo/45603/title/The-Forces-of-Cancer/.
- ↑ Wang, Karin; Cai, Li-Heng; Lan, Bo; Fredberg, Jeffrey J (2016-01-28). "Hidden in the mist no more: physical force in cell biology" (in en). Nature Methods 13 (2): 124–125. doi:10.1038/nmeth.3744. ISSN 1548-7105. PMID 26820546.
- ↑ Pickup, Michael W.; Mouw, Janna K.; Weaver, Valerie M. (2014-12-01). "The extracellular matrix modulates the hallmarks of cancer" (in en). EMBO Reports 15 (12): 1243–1253. doi:10.15252/embr.201439246. ISSN 1469-221X. PMID 25381661.
- ↑ Bissell, Mina J.; Hall, H.Glenn; Parry, Gordon (1982). "How does the extracellular matrix direct gene expression?". Journal of Theoretical Biology 99 (1): 31–68. doi:10.1016/0022-5193(82)90388-5. PMID 6892044. Bibcode: 1982JThBi..99...31B.
- ↑ 6.0 6.1 Gene expression during normal and malignant differentiation. Andersson, Leif C., Gahmberg, C. G., Ekblom, P., Sigrid Jusélius stiftelse.. London: Academic Press. 1985. ISBN 978-0120594900. OCLC 11972757. https://archive.org/details/geneexpressiondu0000sigr.
- ↑ Helmlinger, Gabriel; Netti, Paolo A.; Lichtenbeld, Hera C.; Melder, Robert J.; Jain, Rakesh K. (1997-08-01). "Solid stress inhibits the growth of multicellular tumor spheroids" (in en). Nature Biotechnology 15 (8): 778–783. doi:10.1038/nbt0897-778. ISSN 1546-1696. PMID 9255794.
- ↑ Nelson, Celeste M.; Bissell, Mina J. (2006-10-09). "Of Extracellular Matrix, Scaffolds, and Signaling: Tissue Architecture Regulates Development, Homeostasis, and Cancer". Annual Review of Cell and Developmental Biology 22 (1): 287–309. doi:10.1146/annurev.cellbio.22.010305.104315. ISSN 1081-0706. PMID 16824016.
- ↑ Lancaster, Madeline A.; Knoblich, Juergen A. (2014-07-18). "Organogenesis in a dish: Modeling development and disease using organoid technologies" (in en). Science 345 (6194): 1247125. doi:10.1126/science.1247125. ISSN 0036-8075. PMID 25035496.
- ↑ Jin, Ketao; Teng, Lisong; Shen, Yanping; He, Kuifeng; Xu, Zhenzhen; Li, Guangliang (2010-07-01). "Patient-derived human tumour tissue xenografts in immunodeficient mice: a systematic review" (in en). Clinical and Translational Oncology 12 (7): 473–480. doi:10.1007/s12094-010-0540-6. ISSN 1699-048X. PMID 20615824.
- ↑ Paszek, Matthew J.; Zahir, Nastaran; Johnson, Kandice R.; Lakins, Johnathon N.; Rozenberg, Gabriela I.; Gefen, Amit; Reinhart-King, Cynthia A.; Margulies, Susan S. et al. (September 2005). "Tensional homeostasis and the malignant phenotype". Cancer Cell 8 (3): 241–254. doi:10.1016/j.ccr.2005.08.010. PMID 16169468.
- ↑ Trepat, Xavier (2011-10-24). "Viewpoint: Forcing Tumor Arrest" (in en-US). Physics 4: 85. doi:10.1103/physics.4.85.
- ↑ Montel, Fabien (2011). "Stress Clamp Experiments on Multicellular Tumor Spheroids". Physical Review Letters 107 (18): 188102. doi:10.1103/physrevlett.107.188102. PMID 22107677. Bibcode: 2011PhRvL.107r8102M.
- ↑ Cheng, Gang; Tse, Janet; Jain, Rakesh K.; Munn, Lance L. (2009-02-27). "Micro-Environmental Mechanical Stress Controls Tumor Spheroid Size and Morphology by Suppressing Proliferation and Inducing Apoptosis in Cancer Cells". PLOS ONE 4 (2): e4632. doi:10.1371/journal.pone.0004632. ISSN 1932-6203. PMID 19247489. Bibcode: 2009PLoSO...4.4632C.
- ↑ Olcum, Melis; Ozcivici, Engin (2014-10-14). "Daily application of low magnitude mechanical stimulus inhibits the growth of MDA-MB-231 breast cancer cells in vitro". Cancer Cell International 14 (1): 102. doi:10.1186/s12935-014-0102-z. ISSN 1475-2867. PMID 25349533.
- ↑ Plodinec, Marija; Loparic, Marko; Monnier, Christophe A.; Obermann, Ellen C.; Zanetti-Dallenbach, Rosanna; Oertle, Philipp; Hyotyla, Janne T.; Aebi, Ueli et al. (2013-01-29). "The Nanomechanical Signature of Breast Cancer". Biophysical Journal 104 (2): 321a. doi:10.1016/j.bpj.2012.11.1779. Bibcode: 2013BpJ...104..321P.
- ↑ 17.0 17.1 Fuhrmann, A; Staunton, J R; Nandakumar, V; Banyai, N; Davies, P C W; Ros, R (2011). "AFM stiffness nanotomography of normal, metaplastic and dysplastic human esophageal cells". Physical Biology 8 (1): 015007. doi:10.1088/1478-3975/8/1/015007. PMID 21301067. Bibcode: 2011PhBio...8a5007F.
- ↑ Lekka, Małgorzata; Pogoda, Katarzyna; Gostek, Justyna; Klymenko, Olesya; Prauzner-Bechcicki, Szymon; Wiltowska-Zuber, Joanna; Jaczewska, Justyna; Lekki, Janusz et al. (2012). "Cancer cell recognition – Mechanical phenotype". Micron 43 (12): 1259–1266. doi:10.1016/j.micron.2012.01.019. PMID 22436422.
- ↑ Cross, Sarah E; Jin, Yu-Sheng; Tondre, Julianne; Wong, Roger; Rao, JianYu; Gimzewski, James K (2008). "AFM-based analysis of human metastatic cancer cells". Nanotechnology 19 (38): 384003. doi:10.1088/0957-4484/19/38/384003. PMID 21832563. Bibcode: 2008Nanot..19L4003C.
- ↑ Xu, Wenwei; Mezencev, Roman; Kim, Byungkyu; Wang, Lijuan; McDonald, John; Sulchek, Todd (2012-10-04). "Cell Stiffness Is a Biomarker of the Metastatic Potential of Ovarian Cancer Cells". PLOS ONE 7 (10): e46609. doi:10.1371/journal.pone.0046609. ISSN 1932-6203. PMID 23056368. Bibcode: 2012PLoSO...746609X.
- ↑ Brossel, Rémy; Yahi, Alexandre; David, Stéphane; Velasquez, Laura Moreno; Guinebretière, Jean-Marc (2016-04-21). "Mechanical Signals Inhibit Growth of a Grafted Tumor In Vivo: Proof of Concept". PLOS ONE 11 (4): e0152885. doi:10.1371/journal.pone.0152885. ISSN 1932-6203. PMID 27100674. Bibcode: 2016PLoSO..1152885B.
- ↑ "Commission européenne : CORDIS : Projets et résultats : Imaging the Force of Cancer". http://cordis.europa.eu/project/rcn/199748_fr.html.
- ↑ Serwane, Friedhelm; Mongera, Alessandro; Rowghanian, Payam; Kealhofer, David A.; Lucio, Adam A.; Hockenbery, Zachary M.; Campàs, Otger (2017). "In vivo quantification of spatially-varying mechanical properties in developing tissues". Nature Methods 14 (2): 181–186. doi:10.1038/nmeth.4101. ISSN 1548-7091. PMID 27918540.
- ↑ Mariappan, Yogesh K; Glaser, Kevin J; Ehman, Richard L (2010). "Magnetic resonance elastography: A review". Clinical Anatomy 23 (5): 497–511. doi:10.1002/ca.21006. ISSN 0897-3806. PMID 20544947.
- ↑ Larrat, Benoît (2010). "Méthodes de quantification des déplacements en Imagerie par Résonance Magnétique et leurs applications pour la caractérisation mécanique des tissus mous et le guidage de la thérapie par ultrasons focalisés (Doctoral dissertation, Paris 7).". https://hal-univ-diderot.archives-ouvertes.fr/file/index/docid/560381/filename/benoit_Larrat_-_final.pdf.
- ↑ Levental, Kandice R.; Yu, Hongmei; Kass, Laura; Lakins, Johnathon N.; Egeblad, Mikala; Erler, Janine T.; Fong, Sheri F.T.; Csiszar, Katalin et al. (2009-11-25). "Matrix Crosslinking Forces Tumor Progression by Enhancing Integrin Signaling" (in en). Cell 139 (5): 891–906. doi:10.1016/j.cell.2009.10.027. ISSN 0092-8674. PMID 19931152.
- ↑ Ingber, Donald E. (2006-05-01). "Cellular mechanotransduction: putting all the pieces together again" (in en). The FASEB Journal 20 (7): 811–827. doi:10.1096/fj.05-5424rev. ISSN 0892-6638. PMID 16675838.
- ↑ Engler, Adam J.; Griffin, Maureen A.; Sen, Shamik; Bönnemann, Carsten G.; Sweeney, H. Lee; Discher, Dennis E. (2004-09-13). "Myotubes differentiate optimally on substrates with tissue-like stiffness: pathological implications for soft or stiff microenvironments" (in en). J Cell Biol 166 (6): 877–887. doi:10.1083/jcb.200405004. ISSN 0021-9525. PMID 15364962.
- ↑ Georges, Penelope C.; Janmey, Paul A. (2005-04-01). "Cell type-specific response to growth on soft materials" (in en). Journal of Applied Physiology 98 (4): 1547–1553. doi:10.1152/japplphysiol.01121.2004. ISSN 8750-7587. PMID 15772065.
- ↑ Kumar, Sanjay; Weaver, Valerie M. (2009-06-01). "Mechanics, malignancy, and metastasis: The force journey of a tumor cell" (in en). Cancer and Metastasis Reviews 28 (1–2): 113–127. doi:10.1007/s10555-008-9173-4. ISSN 0167-7659. PMID 19153673.
- ↑ Denais, Celine; Lammerding, Jan (2014). "Nuclear Mechanics in Cancer" (in en). Cancer Biology and the Nuclear Envelope. Advances in Experimental Medicine and Biology. 773. Springer, New York, NY. pp. 435–470. doi:10.1007/978-1-4899-8032-8_20. ISBN 9781489980311.
- ↑ Irons, Linda; Xie, Leike; Owen, Markus; Hill, Michael A.; Martinez-Lemus, Luis A.; Glinski, Olga; Glinsky, Vladislav V.; O’Dea, Reuben et al. (2017-04-01). "Utilization of mechano-biological models to predict cell adhesion interactions between bone marrow endothelial cells and breast cancer cells." (in en). The FASEB Journal 31 (1 Supplement): 860.1. ISSN 0892-6638. http://www.fasebj.org/content/31/1_Supplement/860.1.
- ↑ 33.0 33.1 Stylianopoulos, Triantafyllos (2017-02-01). "The Solid Mechanics of Cancer and Strategies for Improved Therapy". Journal of Biomechanical Engineering 139 (2): 021004. doi:10.1115/1.4034991. ISSN 0148-0731. PMID 27760260.
- ↑ "Cancer : les cellules sous pression, par Emmanuel Farge de l'Institut Curie". http://actucancerpancreas.blogspot.fr/2017/03/cancer-les-cellules-sous-pression-par.html.
- ↑ Koch, Thorsten M.; Münster, Stefan; Bonakdar, Navid; Butler, James P.; Fabry, Ben (2012-03-30). "3D Traction Forces in Cancer Cell Invasion". PLOS ONE 7 (3): e33476. doi:10.1371/journal.pone.0033476. ISSN 1932-6203. PMID 22479403. Bibcode: 2012PLoSO...733476K.
- ↑ Alippi, A.; Bettucci, A.; Biagioni, A.; Conclusio, D.; D'Orazio, A.; Germano, M.; Passeri, D. (2012-05-24). "Non linear behaviour of cell tensegrity models". AIP Conference Proceedings 1433 (1): 329–332. doi:10.1063/1.3703199. ISSN 0094-243X. Bibcode: 2012AIPC.1433..329A.
- ↑ Wang, Ning; Tytell, Jessica D.; Ingber, Donald E. (2009). "Mechanotransduction at a distance: mechanically coupling the extracellular matrix with the nucleus" (in En). Nature Reviews Molecular Cell Biology 10 (1): 75–82. doi:10.1038/nrm2594. ISSN 1471-0080. PMID 19197334.
- ↑ Pegoraro, Adrian F.; Fredberg, Jeffrey J.; Park, Jin-Ah (2016). "Problems in biology with many scales of length: Cell–cell adhesion and cell jamming in collective cellular migration". Experimental Cell Research 343 (1): 54–59. doi:10.1016/j.yexcr.2015.10.036. PMID 26546401.
- ↑ Sawyers, Charles L. (1999-04-29). "Chronic Myeloid Leukemia". New England Journal of Medicine 340 (17): 1330–1340. doi:10.1056/nejm199904293401706. ISSN 0028-4793. PMID 10219069.
- ↑ Cook, Jason R.; Carta, Luca; Bénard, Ludovic; Chemaly, Elie R.; Chiu, Emily; Rao, Satish K.; Hampton, Thomas G.; Yurchenco, Peter et al. (2014-03-03). "Abnormal muscle mechanosignaling triggers cardiomyopathy in mice with Marfan syndrome" (in en). Journal of Clinical Investigation 124 (3): 1329–39. doi:10.1172/jci71059. ISSN 0021-9738. PMID 24531548.
- ↑ Dinicola, Simona; D'Anselmi, Fabrizio; Pasqualato, Alessia; Proietti, Sara; Lisi, Elisabetta; Cucina, Alessandra; Bizzarri, Mariano (2011-02-14). "A Systems Biology Approach to Cancer: Fractals, Attractors, and Nonlinear Dynamics". OMICS: A Journal of Integrative Biology 15 (3): 93–104. doi:10.1089/omi.2010.0091. PMID 21319994.
- ↑ Mandelbrot, Benoit (1967-05-05). "How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension" (in en). Science 156 (3775): 636–638. doi:10.1126/science.156.3775.636. ISSN 0036-8075. PMID 17837158. Bibcode: 1967Sci...156..636M. http://ena.lp.edu.ua:8080/handle/ntb/52473.
- ↑ Lefebvre, Françoise; Benali, Habib; Gilles, René; Kahn, Edmond; Di Paola, Robert (1995-04-01). "A fractal approach to the segmentation of microcalcifications in digital mammograms" (in en). Medical Physics 22 (4): 381–390. doi:10.1118/1.597473. ISSN 2473-4209. PMID 7609718. Bibcode: 1995MedPh..22..381L.
- ↑ Baish, James W.; Jain, Rakesh K. (2000-07-15). "Fractals and Cancer" (in en). Cancer Research 60 (14): 3683–3688. ISSN 0008-5472. PMID 10919633. http://cancerres.aacrjournals.org/content/60/14/3683.
- ↑ Sokolov, Igor; Dokukin, Maxim E. (2017). "Fractal Analysis of Cancer Cell Surface" (in en). Cancer Nanotechnology. Methods in Molecular Biology. 1530. Humana Press, New York, NY. pp. 229–245. doi:10.1007/978-1-4939-6646-2_13. ISBN 9781493966448.
- ↑ Li, H.; Liu, K. J. R.; Lo, S. C. B. (December 1997). "Fractal modeling and segmentation for the enhancement of microcalcifications in digital mammograms". IEEE Transactions on Medical Imaging 16 (6): 785–798. doi:10.1109/42.650875. ISSN 0278-0062. PMID 9533579.
- ↑ Miyazawa, Ayako; Ito, Satoru; Asano, Shuichi; Tanaka, Ichidai; Sato, Mitsuo; Kondo, Masashi; Hasegawa, Yoshinori (2018). "Regulation of PD-L1 expression by matrix stiffness in lung cancer cells". Biochemical and Biophysical Research Communications 495 (3): 2344–2349. doi:10.1016/j.bbrc.2017.12.115. ISSN 1090-2104. PMID 29274784.
- ↑ Jiang, Hong; Hegde, Samarth; Knolhoff, Brett L.; Zhu, Yu; Herndon, John M.; Meyer, Melissa A.; Nywening, Timothy M.; Hawkins, William G. et al. (2016). "Targeting Focal Adhesion Kinase Renders Pancreatic Cancers Responsive to Checkpoint Immunotherapy". Nature Medicine 22 (8): 851–860. doi:10.1038/nm.4123. PMID 27376576.
- ↑ Liu, Liyu; Duclos, Guillaume; Sun, Bo; Lee, Jeongseog; Wu, Amy; Kam, Yoonseok; Sontag, Eduardo D.; Stone, Howard A. et al. (2013-01-29). "Minimization of thermodynamic costs in cancer cell invasion" (in en). Proceedings of the National Academy of Sciences 110 (5): 1686–1691. doi:10.1073/pnas.1221147110. ISSN 0027-8424. PMID 23319630. Bibcode: 2013PNAS..110.1686L.
- ↑ Savage, Van M.; Herman, Alexander B.; West, Geoffrey B.; Leu, Kevin (February 2013). "Using fractal geometry and universal growth curves as diagnostics for comparing tumor vasculature and metabolic rate with healthy tissue and for predicting responses to drug therapies". Discrete and Continuous Dynamical Systems - Series B 18 (4): 1077–1108. doi:10.3934/dcdsb.2013.18.1077. PMID 24204201.
- ↑ Pokorný, J. (2011). "Electrodynamic activity of healthy and cancer cells" (in en). Journal of Physics: Conference Series 329 (1): 012007. doi:10.1088/1742-6596/329/1/012007. ISSN 1742-6596. Bibcode: 2011JPhCS.329a2007P.
- ↑ Lewis, Nathan E.; Abdel-Haleem, Alyaa M. (2013). "The evolution of genome-scale models of cancer metabolism" (in English). Frontiers in Physiology 4: 237. doi:10.3389/fphys.2013.00237. ISSN 1664-042X. PMID 24027532.
- ↑ Betancourt-Mar, J.A.; Llanos-Pérez, J.A.; Cocho, G.; Mansilla, R.; Martin, R.R.; Montero, S.; Nieto-Villar, J.M. (2017). "Phase transitions in tumor growth: IV relationship between metabolic rate and fractal dimension of human tumor cells". Physica A: Statistical Mechanics and Its Applications 473: 344–351. doi:10.1016/j.physa.2016.12.089. Bibcode: 2017PhyA..473..344B.
- ↑ (in en) The Law of Bone Remodelling | Julius Wolff | Springer. Springer. 1986. ISBN 9783642710339. https://www.springer.com/la/book/9783642710339.
- ↑ Thompson, D'Arcy Wentworth (1917). On growth and form. MBLWHOI Library. Cambridge [Eng.] University press. https://archive.org/details/ongrowthform1917thom.
- ↑ Cox, Jafna L.; Chiasson, David A.; Gotlieb, Avrum I. (1991). "Stranger in a strange land: The pathogenesis of saphenous vein graft stenosis with emphasis on structural and functional differences between veins and arteries". Progress in Cardiovascular Diseases 34 (1): 45–68. doi:10.1016/0033-0620(91)90019-i. PMID 2063013.
- ↑ Maffini, Maricel V.; Soto, Ana M.; Calabro, Janine M.; Ucci, Angelo A.; Sonnenschein, Carlos (2004-03-15). "The stroma as a crucial target in rat mammary gland carcinogenesis" (in en). Journal of Cell Science 117 (8): 1495–1502. doi:10.1242/jcs.01000. ISSN 0021-9533. PMID 14996910.
- ↑ Barcellos-Hoff, Mary Helen; Ravani, Shraddha A. (2000-03-01). "Irradiated Mammary Gland Stroma Promotes the Expression of Tumorigenic Potential by Unirradiated Epithelial Cells" (in en). Cancer Research 60 (5): 1254–1260. ISSN 0008-5472. PMID 10728684. http://cancerres.aacrjournals.org/content/60/5/1254.
- ↑ Illmensee, K; Mintz, B (March 1976). "Totipotency and normal differentiation of single teratocarcinoma cells cloned by injection into blastocysts.". Proceedings of the National Academy of Sciences of the United States of America 73 (2): 549–553. doi:10.1073/pnas.73.2.549. ISSN 0027-8424. PMID 1061157. Bibcode: 1976PNAS...73..549I.
- ↑ Hochedlinger, Konrad; Blelloch, Robert; Brennan, Cameron; Yamada, Yasuhiro; Kim, Minjung; Chin, Lynda; Jaenisch, Rudolf (2004-08-01). "Reprogramming of a melanoma genome by nuclear transplantation" (in en). Genes & Development 18 (15): 1875–1885. doi:10.1101/gad.1213504. ISSN 0890-9369. PMID 15289459.
- ↑ Maffini, Maricel V.; Calabro, Janine M.; Soto, Ana M.; Sonnenschein, Carlos (2005). "Stromal Regulation of Neoplastic Development". The American Journal of Pathology 167 (5): 1405–1410. doi:10.1016/S0002-9440(10)61227-8. ISSN 0002-9440. PMID 16251424.
- ↑ McCullough, Karen D.; Coleman, William B.; Ricketts, Sharon L.; Wilson, Julie W.; Smith, Gary J.; Grisham, Joe W. (1998-12-22). "Plasticity of the neoplastic phenotype in vivo is regulated by epigenetic factors" (in en). Proceedings of the National Academy of Sciences 95 (26): 15333–15338. doi:10.1073/pnas.95.26.15333. ISSN 0027-8424. PMID 9860969. Bibcode: 1998PNAS...9515333M.
- ↑ Miller, Callie Johnson; Davidson, Lance A. (2013). "The interplay between cell signalling and mechanics in developmental processes" (in En). Nature Reviews Genetics 14 (10): 733–744. doi:10.1038/nrg3513. ISSN 1471-0064. PMID 24045690.
- ↑ Mammoto, Tadanori; Ingber, Donald E. (2010-05-01). "Mechanical control of tissue and organ development" (in en). Development 137 (9): 1407–1420. doi:10.1242/dev.024166. ISSN 0950-1991. PMID 20388652.
- ↑ Thorne, Jeffrey T.; Segal, Thalia R.; Chang, Sydney; Jorge, Soledad; Segars, James H.; Leppert, Phyllis C. (2015-01-01). "Dynamic Reciprocity Between Cells and Their Microenvironment in Reproduction1" (in en). Biology of Reproduction 92 (1): 25. doi:10.1095/biolreprod.114.121368. ISSN 0006-3363. PMID 25411389.
- ↑ Pokorný, Jiří; Foletti, Alberto; Kobilková, Jitka; Jandová, Anna; Vrba, Jan; Vrba, Jan; Nedbalová, Martina; Čoček, Aleš et al. (2013). "Biophysical Insights into Cancer Transformation and Treatment" (in en). The Scientific World Journal 2013: 195028. doi:10.1155/2013/195028. PMID 23844381.
Annexes
Related articles
External links
- United States : National Cancer Institute (NCI) [archive]
- Singapore : Mechanobiology Institute (MBI) [archive] – National University of Singapore
- Europe : Imaging the Force of Cancer [archive], H2020
- Journal : Convergent Science Physical Oncology [archive]
 |