Arcsine distribution

Short description: Type of probability distribution

Arcsine

Probability density function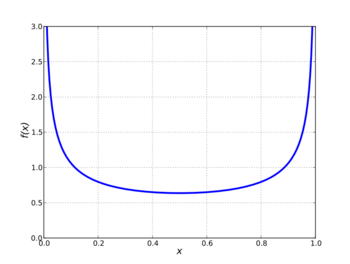
Cumulative distribution function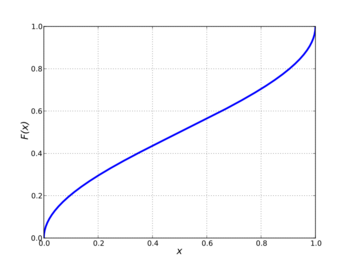
Parameters	none
Support	[math]\displaystyle{ x \in [0,1] }[/math]
PDF	[math]\displaystyle{ f(x) = \frac{1}{\pi\sqrt{x(1-x)}} }[/math]
CDF	[math]\displaystyle{ F(x) = \frac{2}{\pi}\arcsin\left(\sqrt x \right) }[/math]
Mean	[math]\displaystyle{ \frac{1}{2} }[/math]
Median	[math]\displaystyle{ \frac{1}{2} }[/math]
Mode	[math]\displaystyle{ x \in \{0,1\} }[/math]
Variance	[math]\displaystyle{ \tfrac{1}{8} }[/math]
Skewness	[math]\displaystyle{ 0 }[/math]
Kurtosis	[math]\displaystyle{ -\tfrac{3}{2} }[/math]
Entropy	[math]\displaystyle{ \ln \tfrac{\pi}{4} }[/math]
MGF	[math]\displaystyle{ 1 +\sum_{k=1}^{\infty} \left( \prod_{r=0}^{k-1} \frac{2r+1}{2r+2} \right) \frac{t^k}{k!} }[/math]
CF	[math]\displaystyle{ {}_1F_1(\tfrac{1}{2}; 1; i\,t)\ }[/math]

In probability theory, the arcsine distribution is the probability distribution whose cumulative distribution function involves the arcsine and the square root:

[math]\displaystyle{ F(x) = \frac{2}{\pi}\arcsin\left(\sqrt x\right)=\frac{\arcsin(2x-1)}{\pi}+\frac{1}{2} }[/math]

for 0 ≤ x ≤ 1, and whose probability density function is

[math]\displaystyle{ f(x) = \frac{1}{\pi\sqrt{x(1-x)}} }[/math]

on (0, 1). The standard arcsine distribution is a special case of the beta distribution with α = β = 1/2. That is, if [math]\displaystyle{ X }[/math] is an arcsine-distributed random variable, then [math]\displaystyle{ X \sim {\rm Beta}\bigl(\tfrac{1}{2},\tfrac{1}{2}\bigr) }[/math]. By extension, the arcsine distribution is a special case of the Pearson type I distribution.

The arcsine distribution appears in the Lévy arcsine law, in the Erdős arcsine law, and as the Jeffreys prior for the probability of success of a Bernoulli trial.

Generalization

Arcsine – bounded support

Parameters	[math]\displaystyle{ -\infty \lt a \lt b \lt \infty \, }[/math]
Support	[math]\displaystyle{ x \in [a,b] }[/math]
PDF	[math]\displaystyle{ f(x) = \frac{1}{\pi\sqrt{(x-a)(b-x)}} }[/math]
CDF	[math]\displaystyle{ F(x) = \frac{2}{\pi}\arcsin\left(\sqrt \frac{x-a}{b-a} \right) }[/math]
Mean	[math]\displaystyle{ \frac{a+b}{2} }[/math]
Median	[math]\displaystyle{ \frac{a+b}{2} }[/math]
Mode	[math]\displaystyle{ x \in {a,b} }[/math]
Variance	[math]\displaystyle{ \tfrac{1}{8}(b-a)^2 }[/math]
Skewness	[math]\displaystyle{ 0 }[/math]
Kurtosis	[math]\displaystyle{ -\tfrac{3}{2} }[/math]

Arbitrary bounded support

The distribution can be expanded to include any bounded support from a ≤ x ≤ b by a simple transformation

[math]\displaystyle{ F(x) = \frac{2}{\pi}\arcsin\left(\sqrt \frac{x-a}{b-a} \right) }[/math]

for a ≤ x ≤ b, and whose probability density function is

[math]\displaystyle{ f(x) = \frac{1}{\pi\sqrt{(x-a)(b-x)}} }[/math]

on (a, b).

Shape factor

The generalized standard arcsine distribution on (0,1) with probability density function

[math]\displaystyle{ f(x;\alpha) = \frac{\sin \pi\alpha}{\pi}x^{-\alpha}(1-x)^{\alpha-1} }[/math]

is also a special case of the beta distribution with parameters [math]\displaystyle{ {\rm Beta}(1-\alpha,\alpha) }[/math].

Note that when [math]\displaystyle{ \alpha = \tfrac{1}{2} }[/math] the general arcsine distribution reduces to the standard distribution listed above.

Properties

• Arcsine distribution is closed under translation and scaling by a positive factor
  • If [math]\displaystyle{ X \sim {\rm Arcsine}(a,b) \ \text{then } kX+c \sim {\rm Arcsine}(ak+c,bk+c) }[/math]
• The square of an arcsine distribution over (-1, 1) has arcsine distribution over (0, 1)
  • If [math]\displaystyle{ X \sim {\rm Arcsine}(-1,1) \ \text{then } X^2 \sim {\rm Arcsine}(0,1) }[/math]
• The coordinates of points uniformly selected on a circle of radius [math]\displaystyle{ r }[/math] centered at the origin (0, 0), have an [math]\displaystyle{ {\rm Arcsine}(-r,r) }[/math] distribution
  • For example, if we select a point uniformly on the circumference, [math]\displaystyle{ U \sim {\rm Uniform}(0,2\pi r) }[/math], we have that the point's x coordinate distribution is [math]\displaystyle{ r \cdot \cos(U) \sim {\rm Arcsine}(-r,r) }[/math], and its y coordinate distribution is [math]\displaystyle{ r \cdot \sin(U) \sim {\rm Arcsine}(-r,r) }[/math]

Characteristic function

The characteristic function of the arcsine distribution is a confluent hypergeometric function and given as [math]\displaystyle{ {}_1F_1(\tfrac{1}{2}; 1; i\,t)\ }[/math].

Related distributions

• If U and V are i.i.d uniform (−π,π) random variables, then [math]\displaystyle{ \sin(U) }[/math], [math]\displaystyle{ \sin(2U) }[/math], [math]\displaystyle{ -\cos(2U) }[/math], [math]\displaystyle{ \sin(U+V) }[/math] and [math]\displaystyle{ \sin(U-V) }[/math] all have an [math]\displaystyle{ {\rm Arcsine}(-1,1) }[/math] distribution.
• If [math]\displaystyle{ X }[/math] is the generalized arcsine distribution with shape parameter [math]\displaystyle{ \alpha }[/math] supported on the finite interval [a,b] then [math]\displaystyle{ \frac{X-a}{b-a} \sim {\rm Beta}(1-\alpha,\alpha) \ }[/math]
• If X ~ Cauchy(0, 1) then [math]\displaystyle{ \tfrac{1}{1+X^2} }[/math] has a standard arcsine distribution

Further reading

• Hazewinkel, Michiel, ed. (2001), "Arcsine distribution", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Main_Page