Johnson graph

Short description: Class of undirected graphs defined from systems of sets

Johnson graph
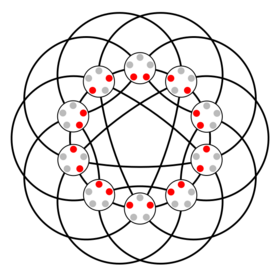The Johnson graph J(5,2)
Named after	Selmer M. Johnson
Vertices	[math]\displaystyle{ \binom{n}{k} }[/math]
Edges	[math]\displaystyle{ \frac{1}{2} k(n - k) \binom{n}{k} }[/math]
Diameter	[math]\displaystyle{ \min(k,n-k) }[/math]
Properties	[math]\displaystyle{ k(n-k) }[/math]-regular Vertex-transitive Distance-transitive Hamilton-connected
Notation	[math]\displaystyle{ J(n,k) }[/math]
Table of graphs and parameters

Johnson graphs are a special class of undirected graphs defined from systems of sets. The vertices of the Johnson graph [math]\displaystyle{ J(n,k) }[/math] are the [math]\displaystyle{ k }[/math]-element subsets of an [math]\displaystyle{ n }[/math]-element set; two vertices are adjacent when the intersection of the two vertices (subsets) contains [math]\displaystyle{ (k-1) }[/math]-elements. Both Johnson graphs and the closely related Johnson scheme are named after Selmer M. Johnson.

Special cases

• [math]\displaystyle{ J(n,1) }[/math] is the complete graph K_n.
• [math]\displaystyle{ J(4,2) }[/math] is the octahedral graph.
• [math]\displaystyle{ J(5,2) }[/math] is the complement of the Petersen graph, hence the line graph of K₅. More generally, for all [math]\displaystyle{ n }[/math], the Johnson graph [math]\displaystyle{ J(n,2) }[/math] is the complement of the Kneser graph [math]\displaystyle{ K(n,2). }[/math]

Graph-theoretic properties

• [math]\displaystyle{ J(n,k) }[/math] is isomorphic to [math]\displaystyle{ J(n,n-k). }[/math]
• For all [math]\displaystyle{ 0 \leq j \leq \operatorname{diam}(J(n,k)) }[/math], any pair of vertices at distance [math]\displaystyle{ j }[/math] share [math]\displaystyle{ k-j }[/math] elements in common.
• [math]\displaystyle{ J(n,k) }[/math] is Hamilton-connected, meaning that every pair of vertices forms the endpoints of a Hamiltonian path in the graph. In particular this means that it has a Hamiltonian cycle.
• It is also known that the Johnson graph [math]\displaystyle{ J(n,k)~ }[/math] is[math]\displaystyle{ ~k(n-k) }[/math]-vertex-connected.
• [math]\displaystyle{ J(n,k) }[/math] forms the graph of vertices and edges of an (n − 1)-dimensional polytope, called a hypersimplex.
• the clique number of [math]\displaystyle{ J(n,k) }[/math] is given by an expression in terms of its least and greatest eigenvalues: [math]\displaystyle{ \omega(J(n,k)) = 1 - \tfrac{\lambda_{\max}}{\lambda_{\min}}. }[/math]
• The chromatic number of [math]\displaystyle{ J(n,k) }[/math] is at most [math]\displaystyle{ n, \chi(J(n,k)) \leq n. }[/math]
• Each Johnson graph is locally grid meaning that the induced subgraph of the neighbors of any vertex is a rook's graph. More precisely, in the Johnson graph [math]\displaystyle{ J(n,k) }[/math], each neighborhood is a [math]\displaystyle{ k\times (n-k) }[/math] rook's graph.

Automorphism group

There is a distance-transitive subgroup of [math]\displaystyle{ \operatorname{Aut}(J(n,k)) }[/math] isomorphic to [math]\displaystyle{ \operatorname{Sym}(n) }[/math]. In fact, [math]\displaystyle{ \operatorname{Aut}(J(n,k)) \cong \operatorname{Sym}(n) }[/math], except that when [math]\displaystyle{ n = 2k \geq 4 }[/math], [math]\displaystyle{ \operatorname{Aut}(J(n,k)) \cong \operatorname{Sym}(n) \times C_2 }[/math].

Intersection array

As a consequence of being distance-transitive, [math]\displaystyle{ J(n,k) }[/math] is also distance-regular. Letting [math]\displaystyle{ d }[/math] denote its diameter, the intersection array of [math]\displaystyle{ J(n,k) }[/math] is given by

[math]\displaystyle{ \left\{ b_{0}, \ldots, b_{d-1}, c_{1}, \ldots c_{d} \right \} }[/math]

where:

[math]\displaystyle{ \begin{align} b_{j} &= (k - j)(n - k - j) && 0 \leq j \lt d \\ c_{j} &= j^2 && 0 \lt j \leq d \end{align} }[/math]

It turns out that unless [math]\displaystyle{ J(n,k) }[/math] is [math]\displaystyle{ J(8,2) }[/math], its intersection array is not shared with any other distinct distance-regular graph; the intersection array of [math]\displaystyle{ J(8,2) }[/math] is shared with three other distance-regular graphs that are not Johnson graphs.

Eigenvalues and Eigenvectors

• The characteristic polynomial of [math]\displaystyle{ J(n,k) }[/math] is given by

[math]\displaystyle{ \phi(x) := \prod_{j=0}^{\operatorname{diam}(J(n,k))} \left (x-A_{n,k}(j)\right )^{\binom{n}{j} - \binom{n}{j-1}}. }[/math]

where [math]\displaystyle{ A_{n,k}(j) = (k-j)(n-k-j)-j. }[/math]

• The eigenvectors of [math]\displaystyle{ J(n,k) }[/math] have an explicit description.

Johnson scheme

The Johnson graph [math]\displaystyle{ J(n,k) }[/math] is closely related to the Johnson scheme, an association scheme in which each pair of k-element sets is associated with a number, half the size of the symmetric difference of the two sets. The Johnson graph has an edge for every pair of sets at distance one in the association scheme, and the distances in the association scheme are exactly the shortest path distances in the Johnson graph.

The Johnson scheme is also related to another family of distance-transitive graphs, the odd graphs, whose vertices are [math]\displaystyle{ k }[/math]-element subsets of an [math]\displaystyle{ (2k+1) }[/math]-element set and whose edges correspond to disjoint pairs of subsets.

Open Problems

The vertex-expansion properties of Johnson graphs, as well as the structure of the corresponding extremal sets of vertices of a given size, are not fully understood. However, an asymptotically tight lower-bound on expansion of large sets of vertices was recently obtained.

In general, determining the chromatic number of a Johnson graph is an open problem.

See also

• Grassmann graph

External links

• Weisstein, Eric W.. "Johnson Graph". http://mathworld.wolfram.com/JohnsonGraph.html. 
• Brouwer, Andries E., Johnson graphs, http://www.win.tue.nl/~aeb/graphs/Johnson.html