3-4-3-12 tiling
| 3-4-3-12 tiling | |
|---|---|

| |
| Type | 2-uniform tiling |
| Vertex configuration |  3.4.3.12 and 3.12.12 |
| Symmetry | p4m, [4,4], (*442) |
| Rotation symmetry | p4, [4,4]+, (442) |
| Properties | 2-uniform, 3-isohedral, 3-isotoxal |
In geometry of the Euclidean plane, the 3-4-3-12 tiling is one of 20 2-uniform tilings of the Euclidean plane by regular polygons, containing regular triangles, squares, and dodecagons, arranged in two vertex configuration: 3.4.3.12 and 3.12.12.[1][2][3][4]
The 3.12.12 vertex figure alone generates a truncated hexagonal tiling, while the 3.4.3.12 only exists in this 2-uniform tiling. There are 2 3-uniform tilings that contain both of these vertex figures among one more.
It has square symmetry, p4m, [4,4], (*442). It is also called a demiregular tiling by some authors.
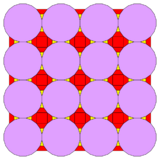
Circle Packing
This 2-uniform tiling can be used as a circle packing. Cyan circles are in contact with 3 other circles (1 cyan, 2 pink), corresponding to the V3.122 planigon, and pink circles are in contact with 4 other circles (2 cyan, 2 pink), corresponding to the V3.4.3.12 planigon. It is homeomorphic to the ambo operation on the tiling, with the cyan and pink gap polygons corresponding to the cyan and pink circles (one dimensional duals to the respective planigons). Both images coincide.
| Circle Packing | Ambo |
|---|---|

|

|
Dual tiling
The dual tiling has kite ('ties') and isosceles triangle faces, defined by face configurations: V3.4.3.12 and V3.12.12. The kites meet in sets of 4 around a center vertex, and the triangles are in pairs making planigon rhombi. Every four kites and four isosceles triangles make a square of side length .
 Dual tiling |
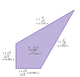 V3.4.3.12 Semiplanigon 120px V3.12.12 Planigon |
This is one of the only dual uniform tilings which only uses planigons (and semiplanigons) containing a 30° angle. Conversely, 3.4.3.12; 3.122 is one of the only uniform tilings in which every vertex is contained on a dodecagon.
Related tilings
It has 2 related 3-uniform tilings that include both 3.4.3.12 and 3.12.12 vertex figures:
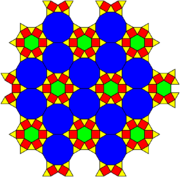 3.4.3.12, 3.12.12, 3.4.6.4 |
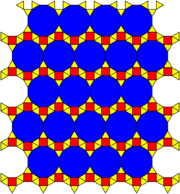 3.4.3.12, 3.12.12, 3.3.4.12 |
 V3.4.3.12, V3.12.12, V3.4.6.4 |
 V3.4.3.12, V3.12.12, V3.3.4.12 |
This tiling can be seen in a series as a lattice of 4n-gons starting from the square tiling. For 16-gons (n=4), the gaps can be filled with isogonal octagons and isosceles triangles.
| 4 | 8 | 12 | 16 | 20 |
|---|---|---|---|---|
 Square tiling Q |
 Truncated square tiling tQ |
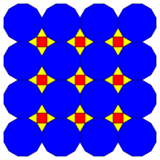 3-4-3-12 tiling |
 Twice-truncated square tiling ttQ |
 20-gons, squares trapezoids, triangles |
Notes
- ↑ Critchlow, pp. 62–67
- ↑ Grünbaum and Shephard 1986, pp. 65–67
- ↑ In Search of Demiregular Tilings #1
- ↑ Chavey (1989)
References
- Keith Critchlow, Order in Space: A design source book, 1970, pp. 62–67
- Ghyka, M. The Geometry of Art and Life, (1946), 2nd edition, New York: Dover, 1977. Demiregular tiling
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. pp. 35–43
- Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman. ISBN 0-7167-1193-1. https://archive.org/details/isbn_0716711931. p. 65
- Sacred Geometry Design Sourcebook: Universal Dimensional Patterns, Bruce Rawles, 1997. pp. 36–37 [1]
External links
- Chavey, D. (1989). "Tilings by Regular Polygons—II: A Catalog of Tilings". Computers & Mathematics with Applications 17: 147–165. doi:10.1016/0898-1221(89)90156-9. https://www.beloit.edu/computerscience/faculty/chavey/catalog/.
- Dutch, Steve. "Uniform Tilings". http://www.uwgb.edu/dutchs/symmetry/uniftil.htm.
- Weisstein, Eric W.. "Demiregular tessellation". http://mathworld.wolfram.com/DemiregularTessellation.html.
- In Search of Demiregular Tilings, Helmer Aslaksen
- n-uniform tilings Brian Galebach, 2-Uniform Tiling 2 of 20
 |
