Circle packing
In geometry, circle packing is the study of the arrangement of circles (of equal or varying sizes) on a given surface such that no overlapping occurs and so that no circle can be enlarged without creating an overlap. The associated packing density, η, of an arrangement is the proportion of the surface covered by the circles. Generalisations can be made to higher dimensions – this is called sphere packing, which usually deals only with identical spheres.
The branch of mathematics generally known as "circle packing" is concerned with the geometry and combinatorics of packings of arbitrarily-sized circles: these give rise to discrete analogs of conformal mapping, Riemann surfaces and the like.
Densest packing
.svg)
In the two-dimensional Euclidean plane, Joseph Louis Lagrange proved in 1773 that the highest-density lattice packing of circles is the hexagonal packing arrangement,[1] in which the centres of the circles are arranged in a hexagonal lattice (staggered rows, like a honeycomb), and each circle is surrounded by six other circles. For circles of diameter D and hexagons of side length D, the hexagon area and the circle area are, respectively:
- [math]\displaystyle{ \begin{align} A_\mathrm{H}&=\frac{3\sqrt{3}}{2}D^2 \\[4pt] A_\mathrm{C}&=\frac{\pi}{4}D^2 \end{align} }[/math]
The area covered within each hexagon by circles is:
- [math]\displaystyle{ A_\mathrm{HC}=3A_\mathrm{C}=\frac{3\pi}{4}D^2 }[/math]
Finally, the packing density is:
- [math]\displaystyle{ \begin{align} \eta=\frac{A_\mathrm{HC}}{A_\mathrm{H}} &= \frac{\frac{3\pi}{4}D^2 }{ \frac{3\sqrt{3}}{2}D^2} \\[4pt] &= \frac{\pi}{2\sqrt{3}} \approx 0.9069 \end{align} }[/math]
In 1890, Axel Thue published a proof that this same density is optimal among all packings, not just lattice packings, but his proof was considered by some to be incomplete. The first rigorous proof is attributed to László Fejes Tóth in 1942.[1][2]
While the circle has a relatively low maximum packing density, it does not have the lowest possible, even among centrally-symmetric convex shapes: the smoothed octagon has a packing density of about 0.902414, the smallest known for centrally-symmetric convex shapes and conjectured to be the smallest possible.[3] (Packing densities of concave shapes such as star polygons can be arbitrarily small.)
Other packings
At the other extreme, Böröczky demonstrated that arbitrarily low density arrangements of rigidly packed circles exist.[4][5]
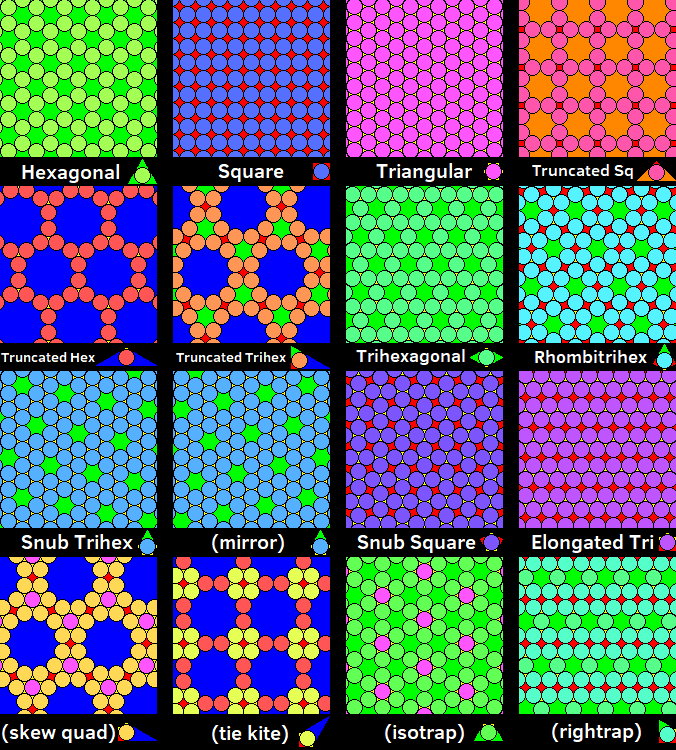
There are eleven circle packings based on the eleven uniform tilings of the plane.[6] In these packings, every circle can be mapped to every other circle by reflections and rotations. The hexagonal gaps can be filled by one circle and the dodecagonal gaps can be filled with seven circles, creating 3-uniform packings. The truncated trihexagonal tiling with both types of gaps can be filled as a 4-uniform packing. The snub hexagonal tiling has two mirror-image forms.
.png)
On the sphere
A related problem is to determine the lowest-energy arrangement of identically interacting points that are constrained to lie within a given surface. The Thomson problem deals with the lowest energy distribution of identical electric charges on the surface of a sphere. The Tammes problem is a generalisation of this, dealing with maximising the minimum distance between circles on sphere. This is analogous to distributing non-point charges on a sphere.
In bounded areas
Packing circles in simple bounded shapes is a common type of problem in recreational mathematics. The influence of the container walls is important, and hexagonal packing is generally not optimal for small numbers of circles. Specific problems of this type that have been studied include:
- Circle packing in a circle
- Circle packing in a square
- Circle packing in a rectangle
- Circle packing in an equilateral triangle
- Circle packing in an isosceles right triangle
See the linked articles for details.
Unequal circles
There are also a range of problems which permit the sizes of the circles to be non-uniform. One such extension is to find the maximum possible density of a system with two specific sizes of circle (a binary system). Only nine particular radius ratios permit compact packing, which is when every pair of circles in contact is in mutual contact with two other circles (when line segments are drawn from contacting circle-center to circle-center, they triangulate the surface).[7] For all these radius ratios a compact packing is known that achieves the maximum possible packing fraction (above that of uniformly-sized discs) for mixtures of discs with that radius ratio.[9] All nine have ratio-specific packings denser than the uniform hexagonal packing, as do some radius ratios without compact packings.[10]
It is also known that if the radius ratio is above 0.742, a binary mixture cannot pack better than uniformly-sized discs.[8] Upper bounds for the density that can be obtained in such binary packings at smaller ratios have also been obtained.[11]
Applications
Quadrature amplitude modulation is based on packing circles into circles within a phase-amplitude space. A modem transmits data as a series of points in a two-dimensional phase-amplitude plane. The spacing between the points determines the noise tolerance of the transmission, while the circumscribing circle diameter determines the transmitter power required. Performance is maximized when the constellation of code points are at the centres of an efficient circle packing. In practice, suboptimal rectangular packings are often used to simplify decoding.
Circle packing has become an essential tool in origami design, as each appendage on an origami figure requires a circle of paper.[12] Robert J. Lang has used the mathematics of circle packing to develop computer programs that aid in the design of complex origami figures.
See also
- Apollonian gasket
- Circle packing in a rectangle
- Circle packing in a square
- Circle packing in a circle
- Inversive distance
- Kepler conjecture
- Malfatti circles
- Packing problem
References
- ↑ 1.0 1.1 Chang, Hai-Chau; Wang, Lih-Chung (2010). "A Simple Proof of Thue's Theorem on Circle Packing". arXiv:1009.4322 [math.MG].
- ↑ Tóth, László Fejes (1942). "Über die dichteste Kugellagerung". Math. Z. 48: 676–684. doi:10.1007/BF01180035.
- ↑ Weisstein, Eric W.. "Smoothed Octagon". http://mathworld.wolfram.com/SmoothedOctagon.html.
- ↑ Böröczky, K. (1964). "Über stabile Kreis- und Kugelsysteme". Annales Universitatis Scientiarum Budapestinensis de Rolando Eötvös Nominatae, Sectio Mathematica 7: 79–82.
- ↑ Kahle, Matthew (2012). "Sparse locally-jammed disk packings". Annals of Combinatorics 16 (4): 773–780. doi:10.1007/s00026-012-0159-0.
- ↑ Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. p. 35-39. ISBN 0-486-23729-X.
- ↑ 7.0 7.1 Tom Kennedy (2006). "Compact packings of the plane with two sizes of discs". Discrete & Computational Geometry 35 (2): 255–267. doi:10.1007/s00454-005-1172-4.
- ↑ 8.0 8.1 Heppes, Aladár (1 August 2003). "Some Densest Two-Size Disc Packings in the Plane". Discrete & Computational Geometry 30 (2): 241–262. doi:10.1007/s00454-003-0007-6.
- ↑ Bédaride, Nicolas; Fernique, Thomas (2022). "Density of binary disc packings: the nine compact packings". Discrete & Computational Geometry 67 (3): 787–810. doi:10.1007/s00454-021-00348-7.
- ↑ Kennedy, Tom (2004-07-21). "Circle Packings". http://math.arizona.edu/~tgk/pack_two_discs/.
- ↑ de Laat, David; de Oliveira Filho, Fernando Mario; Vallentin, Frank (12 June 2012). "Upper bounds for packings of spheres of several radii". Forum of Mathematics, Sigma 2. doi:10.1017/fms.2014.24.
- ↑ TED.com lecture on modern origami "Robert Lang on TED ."
Bibliography
- Wells D (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. pp. 30–31, 167. ISBN 0-14-011813-6. https://archive.org/details/penguindictionar0000well/page/30.
- Stephenson, Kenneth (December 2003). "Circle Packing: A Mathematical Tale". Notices of the American Mathematical Society 50 (11). http://www.math.utk.edu/~kens/Notices_article.pdf.
 |  |
