Ambient space (mathematics)
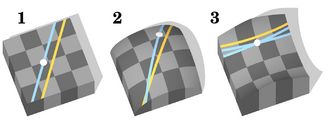
In mathematics, especially in geometry and topology, an ambient space is the space surrounding a mathematical object along with the object itself. For example, a 1-dimensional line [math]\displaystyle{ (l) }[/math] may be studied in isolation —in which case the ambient space of [math]\displaystyle{ l }[/math] is [math]\displaystyle{ l }[/math], or it may be studied as an object embedded in 2-dimensional Euclidean space [math]\displaystyle{ (\mathbb{R}^2) }[/math]—in which case the ambient space of [math]\displaystyle{ l }[/math] is [math]\displaystyle{ \mathbb{R}^2 }[/math], or as an object embedded in 2-dimensional hyperbolic space [math]\displaystyle{ (\mathbb{H}^2) }[/math]—in which case the ambient space of [math]\displaystyle{ l }[/math] is [math]\displaystyle{ \mathbb{H}^2 }[/math]. To see why this makes a difference, consider the statement "Parallel lines never intersect." This is true if the ambient space is [math]\displaystyle{ \mathbb{R}^2 }[/math], but false if the ambient space is [math]\displaystyle{ \mathbb{H}^2 }[/math], because the geometric properties of [math]\displaystyle{ \mathbb{R}^2 }[/math] are different from the geometric properties of [math]\displaystyle{ \mathbb{H}^2 }[/math]. All spaces are subsets of their ambient space.
See also
- Configuration space
- Geometric space
- Manifold and ambient manifold
- Submanifolds and Hypersurfaces
- Riemannian manifolds
- Ricci curvature
- Differential form
References
Further reading
- Schilders, W. H. A.; ter Maten, E. J. W.; Ciarlet, Philippe G. (2005). Numerical Methods in Electromagnetics. Special Volume. Elsevier. pp. 120ff. ISBN 0-444-51375-2.
- Wiggins, Stephen (1992). Chaotic Transport in Dynamical Systems. Berlin: Springer. pp. 209ff. ISBN 3-540-97522-5. https://archive.org/details/chaotictransport0002wigg.
 |