Andrica's conjecture

(a) The function [math]\displaystyle{ A_n }[/math] for the first 100 primes.

(b) The function [math]\displaystyle{ A_n }[/math] for the first 200 primes.

(c) The function [math]\displaystyle{ A_n }[/math] for the first 500 primes.

Graphical proof for Andrica's conjecture for the first (a)100, (b)200 and (c)500 prime numbers. It is conjectured that the function [math]\displaystyle{ A_n }[/math] is always less than 1.

Andrica's conjecture (named after Dorin Andrica) is a conjecture regarding the gaps between prime numbers.

The conjecture states that the inequality

[math]\displaystyle{ \sqrt{p_{n+1}} - \sqrt{p_n} \lt 1 }[/math]

holds for all [math]\displaystyle{ n }[/math], where [math]\displaystyle{ p_n }[/math] is the nth prime number. If [math]\displaystyle{ g_n = p_{n+1} - p_n }[/math] denotes the nth prime gap, then Andrica's conjecture can also be rewritten as

[math]\displaystyle{ g_n \lt 2\sqrt{p_n} + 1. }[/math]

Empirical evidence

Imran Ghory has used data on the largest prime gaps to confirm the conjecture for [math]\displaystyle{ n }[/math] up to 1.3002 × 10¹⁶. Using a table of maximal gaps and the above gap inequality, the confirmation value can be extended exhaustively to 4 × 10¹⁸.

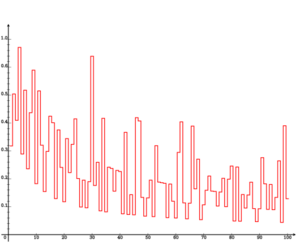
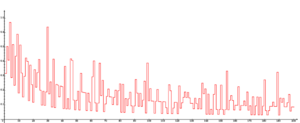
The discrete function [math]\displaystyle{ A_n = \sqrt{p_{n+1}}-\sqrt{p_n} }[/math] is plotted in the figures opposite. The high-water marks for [math]\displaystyle{ A_n }[/math] occur for n = 1, 2, and 4, with A₄ ≈ 0.670873..., with no larger value among the first 10⁵ primes. Since the Andrica function decreases asymptotically as n increases, a prime gap of ever increasing size is needed to make the difference large as n becomes large. It therefore seems highly likely the conjecture is true, although this has not yet been proven.

Generalizations

Value of x in the generalized Andrica's conjecture for the first 100 primes, with the conjectured value of x_min labeled.

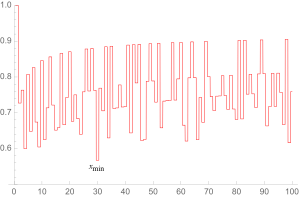
As a generalization of Andrica's conjecture, the following equation has been considered:

[math]\displaystyle{ p _ {n+1} ^ x - p_ n ^ x = 1, }[/math]

where [math]\displaystyle{ p_n }[/math] is the nth prime and x can be any positive number.

The largest possible solution for x is easily seen to occur for n=1, when x_max = 1. The smallest solution for x is conjectured to be x_min ≈ 0.567148... (sequence A038458 in the OEIS) which occurs for n = 30.

This conjecture has also been stated as an inequality, the generalized Andrica conjecture:

[math]\displaystyle{ p _ {n+1} ^ x - p_ n ^ x \lt 1 }[/math] for [math]\displaystyle{ x \lt x_{\min}. }[/math]

See also

• Cramér's conjecture
• Legendre's conjecture
• Firoozbakht's conjecture

References and notes

• Guy, Richard K. (2004). Unsolved problems in number theory (3rd ed.). Springer-Verlag. ISBN 978-0-387-20860-2. 

External links

• Andrica's Conjecture at PlanetMath
• Generalized Andrica conjecture at PlanetMath
• Weisstein, Eric W.. "Andrica's Conjecture". http://mathworld.wolfram.com/AndricasConjecture.html.