Legendre's constant

Short description: Constant of proportionality of prime number density

The first 100,000 elements of the sequence a_n = log(n) − n/π(n) (red line) appear to converge to a value around 1.08366 (blue line).

Later elements up to 10,000,000 of the same sequence a_n = log(n) − n/π(n) (red line) appear to be consistently less than 1.08366 (blue line).

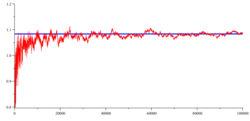
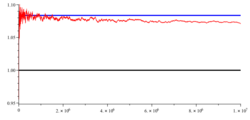
Legendre's constant is a mathematical constant occurring in a formula constructed by Adrien-Marie Legendre to approximate the behavior of the prime-counting function [math]\displaystyle{ \pi(x) }[/math]. The value that corresponds precisely to its asymptotic behavior is now known to be 1.

Examination of available numerical data for known values of [math]\displaystyle{ \pi(x) }[/math] led Legendre to an approximating formula.

Legendre constructed in 1808 the formula

[math]\displaystyle{ \pi(x)\approx\frac{x}{\log(x) - B}, }[/math]

where [math]\displaystyle{ B = 1.08366 }[/math] (OEIS: A228211), as giving an approximation of [math]\displaystyle{ \pi(x) }[/math] with a "very satisfying precision".

Today, one defines the value of [math]\displaystyle{ B }[/math] such that

[math]\displaystyle{ \pi(x)\sim\frac{x}{\log(x) - B}, }[/math]

which is solved by putting

[math]\displaystyle{ B=\lim_{n \to \infty } \left( \log(n) - {n \over \pi(n)} \right), }[/math]

provided that this limit exists.

Not only is it now known that the limit exists, but also that its value is equal to [math]\displaystyle{ 1, }[/math] somewhat less than Legendre's [math]\displaystyle{ 1.08366. }[/math] Regardless of its exact value, the existence of the limit [math]\displaystyle{ B }[/math] implies the prime number theorem.

Pafnuty Chebyshev proved in 1849 that if the limit B exists, it must be equal to 1. An easier proof was given by Pintz in 1980.

It is an immediate consequence of the prime number theorem, under the precise form with an explicit estimate of the error term

[math]\displaystyle{ \pi(x) = \operatorname{Li} (x) + O \left(x e^{-a\sqrt{\log x}}\right) \quad\text{as } x \to \infty }[/math]

(for some positive constant a, where O(…) is the big O notation), as proved in 1899 by Charles de La Vallée Poussin, that B indeed is equal to 1. (The prime number theorem had been proved in 1896, independently by Jacques Hadamard and La Vallée Poussin, but without any estimate of the involved error term).

Being evaluated to such a simple number has made the term Legendre's constant mostly only of historical value, with it often (technically incorrectly) being used to refer to Legendre's first guess 1.08366... instead.

External links

• Weisstein, Eric W.. "Legendre's constant". http://mathworld.wolfram.com/LegendresConstant.html.