Goldbach's conjecture

From HandWiki
Short description: Even integers as sums of two primes
Goldbach's conjecture
Letter Goldbach-Euler.jpg
Letter from Goldbach to Euler dated 7 June 1742 (Latin-German)[1]
FieldNumber theory
Conjectured byChristian Goldbach
Conjectured in1742
Open problemYes
ConsequencesGoldbach's weak conjecture

Goldbach's conjecture is one of the oldest and best-known unsolved problems in number theory and all of mathematics. It states that every even natural number greater than 2 is the sum of two prime numbers.

The conjecture has been shown to hold for all integers less than 4.10×1018[2] but remains unproven despite considerable effort.

History

Origins

On 7 June 1742, the Prussian mathematician Christian Goldbach wrote a letter to Leonhard Euler (letter XLIII),[3] in which he proposed the following conjecture:

Every integer that can be written as the sum of two primes can also be written as the sum of as many primes as one wishes, until all terms are units.

Goldbach was following the now-abandoned convention of considering 1 to be a prime number,[4] so that a sum of units would be a sum of primes. He then proposed a second conjecture in the margin of his letter, which implies the first:[5]

... eine jede Zahl, die grösser ist als 2, ein aggregatum trium numerorum primorum sey.
Every integer greater than 2 can be written as the sum of three primes.

Euler replied in a letter dated 30 June 1742[6] and reminded Goldbach of an earlier conversation they had had ("... so Ew vormals mit mir communicirt haben ..."), in which Goldbach had remarked that the first of those two conjectures would follow from the statement

Every positive even integer can be written as the sum of two primes.

This is in fact equivalent to his second, marginal conjecture. In the letter dated 30 June 1742, Euler stated:[7][8]

Dass ... ein jeder numerus par eine summa duorum primorum sey, halte ich für ein ganz gewisses theorema, ungeachtet ich dasselbe nicht demonstriren kann.
That ... every even integer is a sum of two primes, I regard as a completely certain theorem, although I cannot prove it.

Partial results

The strong Goldbach conjecture is much more difficult than the weak Goldbach conjecture. Using Vinogradov's method, Nikolai Chudakov,[9] Johannes van der Corput,[10] and Theodor Estermann[11] showed that almost all even numbers can be written as the sum of two primes (in the sense that the fraction of even numbers up to some N which can be so written tends towards 1 as N increases). In 1930, Lev Schnirelmann proved that any natural number greater than 1 can be written as the sum of not more than C prime numbers, where C is an effectively computable constant; see Schnirelmann density.[12][13] Schnirelmann's constant is the lowest number C with this property. Schnirelmann himself obtained C < 800000. This result was subsequently enhanced by many authors, such as Olivier Ramaré, who in 1995 showed that every even number n ≥ 4 is in fact the sum of at most 6 primes. The best known result currently stems from the proof of the weak Goldbach conjecture by Harald Helfgott,[14] which directly implies that every even number n ≥ 4 is the sum of at most 4 primes.[15][16]

In 1924, Hardy and Littlewood showed under the assumption of the generalized Riemann hypothesis that the number of even numbers up to X violating the Goldbach conjecture is much less than X​1⁄2 + c for small c.[17]

In 1948, using sieve theory methods, Alfréd Rényi showed that every sufficiently large even number can be written as the sum of a prime and an almost prime with at most K factors.[18] Chen Jingrun showed in 1973 using sieve theory that every sufficiently large even number can be written as the sum of either two primes, or a prime and a semiprime (the product of two primes).[19] See Chen's theorem for further information.

In 1975, Hugh Montgomery and Robert Charles Vaughan showed that "most" even numbers are expressible as the sum of two primes. More precisely, they showed that there exist positive constants c and C such that for all sufficiently large numbers N, every even number less than N is the sum of two primes, with at most CN1 − c exceptions. In particular, the set of even integers that are not the sum of two primes has density zero.

In 1951, Yuri Linnik proved the existence of a constant K such that every sufficiently large even number is the sum of two primes and at most K powers of 2. János Pintz and Imre Ruzsa found in 2020 that K = 8 works.[20] Assuming the generalized Riemann hypothesis, K = 7 also works, as shown by Roger Heath-Brown and Jan-Christoph Schlage-Puchta in 2002.[21]

A proof for the weak conjecture was submitted in 2013 by Harald Helfgott to Annals of Mathematics Studies series. Although the article was accepted, Helfgott decided to undertake the major modifications suggested by the referee. Despite several revisions, Helfgott's proof has not yet appeared in a peer-reviewed publication.[22][23][24] The weak conjecture is implied by the strong conjecture, as if n − 3 is a sum of two primes, then n is a sum of three primes. However, the converse implication and thus the strong Goldbach conjecture would remain unproven if Helfgott's proof is correct.

Computational results

For small values of n, the strong Goldbach conjecture (and hence the weak Goldbach conjecture) can be verified directly. For instance, in 1938, Nils Pipping laboriously verified the conjecture up to n = 100000.[25] With the advent of computers, many more values of n have been checked; T. Oliveira e Silva ran a distributed computer search that has verified the conjecture for n ≤ 4×1018 (and double-checked up to 4×1017) as of 2013. One record from this search is that 3325581707333960528 is the smallest number that cannot be written as a sum of two primes where one is smaller than 9781.[26]

Cully-Hugill and Dudek prove[27] a (partial and conditional) result on the Riemann hypothesis: there exists a sum of two odd primes in the interval (x, x + 9696 log^2 x] for all x ≥ 2.

In popular culture

Goldbach's Conjecture (Chinese: 哥德巴赫猜想) is the title of the biography of Chinese mathematician and number theorist Chen Jingrun, written by Xu Chi.

The conjecture is a central point in the plot of the 1992 novel Uncle Petros and Goldbach's Conjecture by Greek author Apostolos Doxiadis, in the short story "Sixty Million Trillion Combinations" by Isaac Asimov and also in the 2008 mystery novel No One You Know by Michelle Richmond.[28]

Goldbach's conjecture is part of the plot of the 2007 Spanish film Fermat's Room.

Goldbach conjecture is found as the main topic of research of actress Ella Rumpf playing Marguerite in the late movie in cinetheatres Le Théorème de Marguerite (fr).[29]

Formal statement

Each of the three conjectures has a natural analog in terms of the modern definition of a prime, under which 1 is excluded. A modern version of the first conjecture is:

Every integer that can be written as the sum of two primes can also be written as the sum of as many primes as one wishes, until either all terms are two (if the integer is even) or one term is three and all other terms are two (if the integer is odd).

A modern version of the marginal conjecture is:

Every integer greater than 5 can be written as the sum of three primes.

And a modern version of Goldbach's older conjecture of which Euler reminded him is:

Every even integer greater than 2 can be written as the sum of two primes.

These modern versions might not be entirely equivalent to the corresponding original statements. For example, if there were an even integer N = p + 1 larger than 4, for p a prime, that could not be expressed as the sum of two primes in the modern sense, then it would be a counterexample to the modern version of the third conjecture (without being a counterexample to the original version). The modern version is thus probably stronger (but in order to confirm that, one would have to prove that the first version, freely applied to any positive even integer n, could not possibly rule out the existence of such a specific counterexample N). In any case, the modern statements have the same relationships with each other as the older statements did. That is, the second and third modern statements are equivalent, and either implies the first modern statement.

The third modern statement (equivalent to the second) is the form in which the conjecture is usually expressed today. It is also known as the "strong", "even", or "binary" Goldbach conjecture. A weaker form of the second modern statement, known as "Goldbach's weak conjecture", the "odd Goldbach conjecture", or the "ternary Goldbach conjecture", asserts that

Every odd integer greater than 7 can be written as the sum of three odd primes.

Heuristic justification

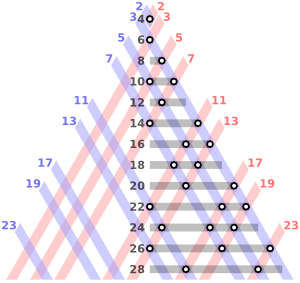
Sums of two primes at the intersections of three lines

Statistical considerations that focus on the probabilistic distribution of prime numbers present informal evidence in favour of the conjecture (in both the weak and strong forms) for sufficiently large integers: the greater the integer, the more ways there are available for that number to be represented as the sum of two or three other numbers, and the more "likely" it becomes that at least one of these representations consists entirely of primes.

Number of ways to write an even number n as the sum of two primes (sequence A002375 in the OEIS)

A very crude version of the heuristic probabilistic argument (for the strong form of the Goldbach conjecture) is as follows. The prime number theorem asserts that an integer m selected at random has roughly a 1/ln m chance of being prime. Thus if n is a large even integer and m is a number between 3 and n/2, then one might expect the probability of m and n − m simultaneously being prime to be 1/ln m ln(n − m). If one pursues this heuristic, one might expect the total number of ways to write a large even integer n as the sum of two odd primes to be roughly

[math]\displaystyle{ \sum_{m=3}^\frac{n}{2} \frac{1}{\ln m} \frac{1}{\ln(n - m)} \approx \frac{n}{2 (\ln n)^2}. }[/math]

Since ln n ≪ √n, this quantity goes to infinity as n increases, and one would expect that every large even integer has not just one representation as the sum of two primes, but in fact very many such representations.

This heuristic argument is actually somewhat inaccurate because it assumes that the events of m and n − m being prime are statistically independent of each other. For instance, if m is odd, then n − m is also odd, and if m is even, then n − m is even, a non-trivial relation because, besides the number 2, only odd numbers can be prime. Similarly, if n is divisible by 3, and m was already a prime other than 3, then n − m would also be coprime to 3 and thus be slightly more likely to be prime than a general number. Pursuing this type of analysis more carefully, G. H. Hardy and John Edensor Littlewood in 1923 conjectured (as part of their Hardy–Littlewood prime tuple conjecture) that for any fixed c ≥ 2, the number of representations of a large integer n as the sum of c primes n = p1 + ⋯ + pc with p1 ≤ ⋯ ≤ pc should be asymptotically equal to

[math]\displaystyle{ \left(\prod_p \frac{p \gamma_{c,p}(n)}{(p - 1)^c}\right) \int_{2 \leq x_1 \leq \cdots \leq x_c: x_1 + \cdots + x_c = n} \frac{dx_1 \cdots dx_{c-1}}{\ln x_1 \cdots \ln x_c}, }[/math]

where the product is over all primes p, and γc,p(n) is the number of solutions to the equation n = q1 + ⋯ + qc mod p in modular arithmetic, subject to the constraints q1, …, qc ≠ 0 mod p. This formula has been rigorously proven to be asymptotically valid for c ≥ 3 from the work of Ivan Matveevich Vinogradov, but is still only a conjecture when c = 2.[citation needed] In the latter case, the above formula simplifies to 0 when n is odd, and to

[math]\displaystyle{ 2 \Pi_2 \left(\prod_{p \mid n; p \geq 3} \frac{p - 1}{p - 2}\right) \int_2^n \frac{dx}{(\ln x)^2} \approx 2 \Pi_2 \left(\prod_{p \mid n; p \geq 3} \frac{p - 1}{p - 2}\right) \frac{n}{(\ln n)^2} }[/math]

when n is even, where Π2 is Hardy–Littlewood's twin prime constant

[math]\displaystyle{ \Pi_2 := \prod_{p\;{\rm prime} \ge 3} \left(1 - \frac{1}{(p-1)^2}\right) \approx 0.66016\,18158\,46869\,57392\,78121\,10014\dots }[/math]

This is sometimes known as the extended Goldbach conjecture. The strong Goldbach conjecture is in fact very similar to the twin prime conjecture, and the two conjectures are believed to be of roughly comparable difficulty.

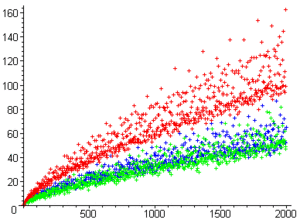
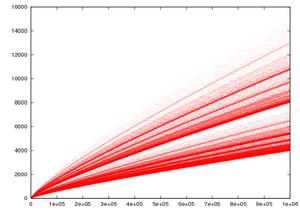
Goldbach's comet; red, blue and green points correspond respectively the values 0, 1 and 2 modulo 3 of the number.

The Goldbach partition function is the function that associates to each even integer the number of ways it can be decomposed into a sum of two primes. Its graph looks like a comet and is therefore called Goldbach's comet.[30]

Goldbach's comet suggests tight upper and lower bounds on the number of representations of an even number as the sum of two primes, and also that the number of these representations depend strongly on the value modulo 3 of the number.

Related problems

Although Goldbach's conjecture implies that every positive integer greater than one can be written as a sum of at most three primes, it is not always possible to find such a sum using a greedy algorithm that uses the largest possible prime at each step. The Pillai sequence tracks the numbers requiring the largest number of primes in their greedy representations.[31]

Similar problems to Goldbach's conjecture exist in which primes are replaced by other particular sets of numbers, such as the squares:

  • It was proven by Lagrange that every positive integer is the sum of four squares. See Waring's problem and the related Waring–Goldbach problem on sums of powers of primes.
  • Hardy and Littlewood listed as their Conjecture I: "Every large odd number (n > 5) is the sum of a prime and the double of a prime".[32] This conjecture is known as Lemoine's conjecture and is also called Levy's conjecture.
  • The Goldbach conjecture for practical numbers, a prime-like sequence of integers, was stated by Margenstern in 1984,[33] and proved by Melfi in 1996:[34] every even number is a sum of two practical numbers.
  • Harvey Dubner proposed a strengthening of the Goldbach conjecture that states that every even integer greater than 4208 is the sum of two twin primes (not necessarily belonging to the same pair).[35][better source needed] Only 34 even integers less than 4208 are not the sum of two twin primes; Dubner has verified computationally that this list is complete up to [math]\displaystyle{ 2\cdot 10^{10}. }[/math][36][verification needed] A proof of this stronger conjecture would not only imply Goldbach's conjecture, but also the twin prime conjecture.

References

  1. ↑ Correspondance mathématique et physique de quelques célèbres géomètres du XVIIIème siècle (Band 1), St.-Pétersbourg 1843, pp. 125–129.
  2. ↑ Oliveira e Silva, Tomás. "Goldbach conjecture verification". https://sweet.ua.pt/tos/goldbach.html. 
  3. ↑ http://www.math.dartmouth.edu/~euler/correspondence/letters/OO0765.pdf[bare URL PDF]
  4. ↑ Weisstein, Eric W.. "Goldbach Conjecture". http://mathworld.wolfram.com/GoldbachConjecture.html. 
  5. ↑ In the printed version published by P. H. Fuss [1] 2 is misprinted as 1 in the marginal conjecture.
  6. ↑ http://eulerarchive.maa.org//correspondence/letters/OO0766.pdf[bare URL PDF]
  7. ↑ Ingham, A. E.. "Popular Lectures". http://www.claymath.org/Popular_Lectures/U_Texas/Riemann_1.pdf. 
  8. ↑ Caldwell, Chris (2008). "Goldbach's conjecture". http://primes.utm.edu/glossary/page.php?sort=goldbachconjecture. 
  9. ↑ Chudakov, Nikolai G. (1937). "О проблеме Гольдбаха". Doklady Akademii Nauk SSSR 17: 335–338. 
  10. ↑ Van der Corput, J. G. (1938). "Sur l'hypothèse de Goldbach" (in fr). Proc. Akad. Wet. Amsterdam 41: 76–80. http://www.dwc.knaw.nl/DL/publications/PU00016746.pdf. 
  11. ↑ Estermann, T. (1938). "On Goldbach's problem: proof that almost all even positive integers are sums of two primes". Proc. London Math. Soc.. 2 44: 307–314. doi:10.1112/plms/s2-44.4.307. 
  12. ↑ Schnirelmann, L. G. (1930). "On the additive properties of numbers", first published in "Proceedings of the Don Polytechnic Institute in Novocherkassk" (in Russian), vol 14 (1930), pp. 3–27, and reprinted in "Uspekhi Matematicheskikh Nauk" (in Russian), 1939, no. 6, 9–25.
  13. ↑ Schnirelmann, L. G. (1933). First published as "Über additive Eigenschaften von Zahlen" in "Mathematische Annalen" (in German), vol. 107 (1933), 649–690, and reprinted as "On the additive properties of numbers" in "Uspekhi Matematicheskikh Nauk" (in Russian), 1940, no. 7, 7–46.
  14. ↑ Helfgott, H. A. (2013). "The ternary Goldbach conjecture is true". arXiv:1312.7748 [math.NT].
  15. ↑ Sinisalo, Matti K. (Oct 1993). "Checking the Goldbach Conjecture up to 4 ⋅ 1011". Mathematics of Computation (American Mathematical Society) 61 (204): 931–934. doi:10.2307/2153264. https://www.ams.org/journals/mcom/1993-61-204/S0025-5718-1993-1185250-6/S0025-5718-1993-1185250-6.pdf. 
  16. ↑ Rassias, M. Th. (2017). Goldbach's Problem: Selected Topics. Springer. 
  17. ↑ See, for example, A new explicit formula in the additive theory of primes with applications I. The explicit formula for the Goldbach and Generalized Twin Prime Problems by Janos Pintz.
  18. ↑ Rényi, A. A. (1948). "On the representation of an even number as the sum of a prime and an almost prime" (in Russian). Izvestiya Akademii Nauk SSSR Seriya Matematicheskaya 12: 57–78. 
  19. ↑ Chen, J. R. (1973). "On the representation of a larger even integer as the sum of a prime and the product of at most two primes". Sci. Sinica 16: 157–176. 
  20. ↑ Pintz, J.; Ruzsa, I. Z. (2020-08-01). "On Linnik's approximation to Goldbach's problem. II" (in en). Acta Mathematica Hungarica 161 (2): 569–582. doi:10.1007/s10474-020-01077-8. ISSN 1588-2632. https://doi.org/10.1007/s10474-020-01077-8. 
  21. ↑ Heath-Brown, D. R.; Puchta, J. C. (2002). "Integers represented as a sum of primes and powers of two". Asian Journal of Mathematics 6 (3): 535–565. doi:10.4310/AJM.2002.v6.n3.a7. Bibcode: 2002math......1299H. 
  22. ↑ Helfgott, H. A. (2013). "Major arcs for Goldbach's theorem". arXiv:1305.2897 [math.NT].
  23. ↑ Helfgott, H. A. (2012). "Minor arcs for Goldbach's problem". arXiv:1205.5252 [math.NT].
  24. ↑ "Harald Andrés Helfgott". Institut de Mathématiques de Jussieu-Paris Rive Gauche. https://webusers.imj-prg.fr/~harald.helfgott/anglais/book.html. 
  25. ↑ Pipping, Nils (1890–1982), "Die Goldbachsche Vermutung und der Goldbach-Vinogradowsche Satz". Acta Acad. Aboensis, Math. Phys. 11, 4–25, 1938.
  26. ↑ Tomás Oliveira e Silva, Goldbach conjecture verification. Retrieved 20 July 2013.
  27. ↑ Michaela Cully-Hugill and Adrian W. Dudek, An explicit mean-value estimate for the PNT in intervals
  28. ↑ "MathFiction: No One You Know (Michelle Richmond)". http://kasmana.people.cofc.edu/MATHFICT/mfview.php?callnumber=mf711. 
  29. ↑ Odile Morain Le Théorème de Marguerite, in franceinfo:culture
  30. ↑ Fliegel, Henry F.; Robertson, Douglas S. (1989). "Goldbach's Comet: the numbers related to Goldbach's Conjecture". Journal of Recreational Mathematics 21 (1): 1–7. 
  31. ↑ Sloane, N. J. A., ed. "Sequence A066352 (Pillai sequence)". OEIS Foundation. https://oeis.org/A066352. 
  32. ↑ Mathematics Magazine, 66:1 (1993): 45–47.
  33. ↑ Margenstern, M. (1984). "Results and conjectures about practical numbers". Comptes rendus de l'Académie des Sciences 299: 895–898. 
  34. ↑ Melfi, G. (1996). "On two conjectures about practical numbers". Journal of Number Theory 56: 205–210. doi:10.1006/jnth.1996.0012. 
  35. ↑ "TWIN PRIME CONJECTURES". https://oeis.org/A007534/a007534.pdf. 
  36. ↑ Sloane, N. J. A., ed. "Sequence A007534 (Even numbers that are not the sum of a pair of twin primes)". OEIS Foundation. https://oeis.org/A007534. 

Further reading

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Goldbach%27s_conjecture&oldid=3712704"