Angle of rotation

The angle of rotation from the black ray to the green segment is 60°, from the black ray to the blue segment is 210°, and from the green to the blue segment is 210° − 60° = 150°. A complete rotation about the center point is equal to 1 turn, 360°, or 2π radians.

Indication of the sign and amount of key angles according to rotation direction

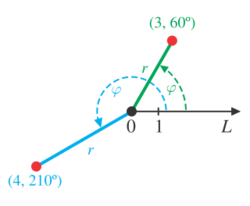
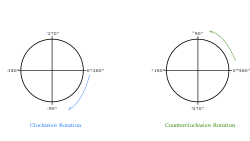
In mathematics, the angle of rotation is a measurement of the amount, of namely angle, that a figure is rotated about a fixed point, often the center of a circle. A clockwise rotation is considered a negative rotation, so that, for instance, a rotation of 310° (counterclockwise) can also be called a rotation of –50° (since 310° + 50° = 360°, a full rotation (turn)). A counterclockwise rotation of more than one complete turn is normally measured modulo 360°, meaning that 360° is subtracted off as many times as possible to leave a non-negative measurement less than 360°.

For example, the carts on a Ferris wheel move along a circle around the center point of that circle. If a cart moves around the wheel once, the angle of rotation is 360°. If the cart was stuck halfway, at the top of the wheel, at that point its angle of rotation was only 180°.

This is also referred to as the "order of symmetry."

Angles are commonly measured in degrees, radians, gons (gradians) and turns, sometimes also in angular mils and binary radians. They are central to polar coordinates and trigonometry.

Properties

If the angle of rotation is denoted as AOR(),

• [math]\displaystyle{ AOR(360a+b)=AOR(b) }[/math] for all integers a and real values b.

See also

• Angular distance
• Hinge
• Plane of rotation
• Rotational symmetry