Astronomy:Titius–Bode law
The Titius–Bode law (sometimes termed simply Bode's law) is a formulaic prediction of spacing between planets in any given solar system. The formula suggests that, extending outward, each planet should be approximately twice as far from the Sun as the one before. The hypothesis correctly anticipated the orbits of Ceres (in the asteroid belt) and Uranus, but failed as a predictor of Neptune's orbit. It is named after Johann Daniel Titius and Johann Elert Bode.
Later work by Blagg and Richardson significantly revised the original formula, and made predictions that were subsequently validated by new discoveries and observations. It is these re-formulations that offer "the best phenomenological representations of distances with which to investigate the theoretical significance of Titius–Bode type Laws".[1]
Original formulation
The law relates the semi-major axis [math]\displaystyle{ ~a_n~ }[/math] of each planet outward from the Sun in units such that the Earth's semi-major axis is equal to 10:
- [math]\displaystyle{ ~a = 4 + x~ }[/math]
where [math]\displaystyle{ ~x = 0, 3, 6, 12, 24, 48, 96, 192, 384, 768 \ldots~ }[/math] such that, with the exception of the first step, each value is twice the previous value. There is another representation of the formula:
- [math]\displaystyle{ ~a = 4 + 3 \times 2^n ~ }[/math]
where [math]\displaystyle{ ~n = -\infty, 0, 1, 2, \ldots~. }[/math] The resulting values can be divided by 10 to convert them into astronomical units (AU), resulting in the expression:
- [math]\displaystyle{ a = 0.4 + 0.3 \times 2^n ~. }[/math]
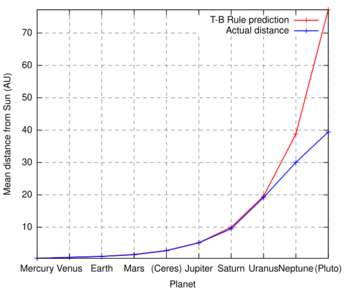
For the far outer planets, beyond Saturn, each planet is predicted to be roughly twice as far from the Sun as the previous object. Whereas the Titius–Bode law predicts Saturn, Uranus, Neptune, and Pluto at about 10, 20, 39, and 77 AU, the actual values are closer to 10, 19, 30, 40 AU.[lower-alpha 1]
This form of the law offered a good first guess; the re-formulations by Blagg and Richardson should be considered accurate.[citation needed]
Origin and history
The first mention of a series approximating Bode's law is found in a textbook by D. Gregory (1715):[2]
- "... supposing the distance of the Earth from the Sun to be divided into ten equal Parts, of these the distance of Mercury will be about four, of Venus seven, of Mars fifteen, of Jupiter fifty two, and that of Saturn ninety five."[3]
A similar sentence, likely paraphrased from Gregory (1715),[2][3] appears in a work published by C. Wolff in 1724.
In 1764, C. Bonnet wrote:[4]
- "We know seventeen planets [that is, major planets and their satellites] that enter into the composition of our solar system; but we are not sure that there are no more."[4][3]
In his 1766 translation of Bonnet's work, J.D. Titius added two of his own paragraphs to the statement above. The insertions were placed at the bottom of page 7 and at the top of page 8. The new paragraph is not in Bonnet's original French text, nor in translations of the work into Italian and English.
There are two parts to Titius's inserted text. The first part explains the succession of planetary distances from the Sun:
- Take notice of the distances of the planets from one another, and recognize that almost all are separated from one another in a proportion which matches their bodily magnitudes. Divide the distance from the Sun to Saturn into 100 parts; then Mercury is separated by four such parts from the Sun, Venus by 4+3=7 such parts, the Earth by 4+6=10, Mars by 4+12=16. But notice that from Mars to Jupiter there comes a deviation from this so exact progression. From Mars there follows a space of 4+24=28 such parts, but so far no planet was sighted there. But should the Lord Architect have left that space empty? Not at all. Let us therefore assume that this space without doubt belongs to the still undiscovered satellites of Mars, let us also add that perhaps Jupiter still has around itself some smaller ones which have not been sighted yet by any telescope. Next to this for us still unexplored space there rises Jupiter's sphere of influence at 4+48=52 parts; and that of Saturn at 4+96=100 parts.[citation needed]
In 1772, J.E. Bode, then aged twenty-five, published an astronomical compendium,[5] in which he included the following footnote, citing Titius (in later editions):[lower-alpha 2][6]
- This latter point seems in particular to follow from the astonishing relation which the known six planets observe in their distances from the Sun. Let the distance from the Sun to Saturn be taken as 100, then Mercury is separated by 4 such parts from the Sun. Venus is 4+3=7. The Earth 4+6=10. Mars 4+12=16. Now comes a gap in this so orderly progression. After Mars there follows a space of 4+24=28 parts, in which no planet has yet been seen. Can one believe that the Founder of the universe had left this space empty? Certainly not. From here we come to the distance of Jupiter by 4+48=52 parts, and finally to that of Saturn by 4+96=100 parts.[6]
These two statements, for all their peculiar expression, and from the radii used for the orbits, seem to stem from an antique algorithm by a cossist.[lower-alpha 3]
Many precedents were found that predate the seventeenth century.[citation needed] Titius was a disciple of the German philosopher C.F. von Wolf (1679–1754), and the second part of the text that Titius inserted into Bonnet's work is in a book by von Wolf (1723),[7] suggesting that Titius learned the relation from him. Twentieth-century literature about Titius–Bode law attributes authorship to von Wolf.[citation needed] A prior version was written by D. Gregory (1702),[8] in which the succession of planetary distances 4, 7, 10, 16, 52, and 100 became a geometric progression with ratio 2. This is the nearest Newtonian formula, which was also cited by Benjamin Martin (1747)[9] and Tomàs Cerdà (c. 1760)[10] years before Titius's expanded translation of Bonnet's book into German (1766). Over the next two centuries, subsequent authors continued to present their own modified versions, apparently unaware of prior work.[1]
Titius and Bode hoped that the law would lead to the discovery of new planets, and indeed the discovery of Uranus and Ceres – both of whose distances fit well with the law – contributed to the law's fame. Neptune's distance was very discrepant, however, and indeed Pluto – no longer considered a planet – is at a mean distance that roughly corresponds to that the Titius–Bode law predicted for the next planet out from Uranus.
When originally published, the law was approximately satisfied by all the planets then known – i.e., Mercury through Saturn – with a gap between the fourth and fifth planets. Vikarius (Johann Friedrich) Wurm (1787) proposed a modified version of the Titius–Bode Law that accounted for the then-known satellites of Jupiter and Saturn, and better predicted the distance for Mercury.[11]
The Titius–Bode law was regarded as interesting, but of no great importance until the discovery of Uranus in 1781, which happens to fit into the series nearly exactly. Based on this discovery, Bode urged his contemporaries to search for a fifth planet. Ceres, the largest object in the asteroid belt, was found at Bode's predicted position in 1801.
Bode's law was widely accepted at that point, until in 1846 Neptune was discovered in a location that does not conform to the law. Simultaneously, due to the large number of asteroids discovered in the belt, Ceres was no longer a major planet. In 1898 the astronomer and logician C.S. Peirce used Bode's law as an example of fallacious reasoning.[12]
The discovery of Pluto in 1930 confounded the issue still further: Although nowhere near its predicted position according to Bode's law, it was very nearly at the position the law had designated for Neptune. The subsequent discovery of the Kuiper belt – and in particular the object Eris, which is more massive than Pluto, yet does not fit Bode's law – further discredited the formula.[13]
Data
The Titius–Bode law predicts planets will be present at specific distances in astronomical units, which can be compared to the observed data for the planets and two dwarf planets in the solar system:
| m | k | T–B rule distance (AU) | Planet | Semimajor axis (AU) | Deviation from prediction1 |
|---|---|---|---|---|---|
| [math]\displaystyle{ -\infty }[/math] | 0 | 0.4 | Mercury | 0.39 | −3.23% |
| 0 | 1 | 0.7 | Venus | 0.72 | +3.33% |
| 1 | 2 | 1.0 | Earth | 1.00 | 0.00% |
| 2 | 4 | 1.6 | Mars | 1.52 | −4.77% |
| 3 | 8 | 2.8 | Ceres2 | 2.77 | −1.16% |
| 4 | 16 | 5.2 | Jupiter | 5.20 | +0.05% |
| 5 | 32 | 10.0 | Saturn | 9.58 | −4.42% |
| 6 | 64 | 19.6 | Uranus | 19.22 | −1.95% |
| – | – | – | Neptune | 30.07 | – |
| 7 | 128 | 38.8 | Pluto2 | 39.48 | +1.02% |
2 Ceres and Pluto are dwarf planets rather than major planets.
Blagg formulation
In 1913, M.A. Blagg, an Oxford astronomer, re-visited the law.[14] She analyzed the orbits of the planetary system and those of the satellite systems of the outer gas giants, Jupiter, Saturn and Uranus. She examined the log of the distances, trying to find the best 'average' difference.
Her analysis resulted in a different formula:
- [math]\displaystyle{ \ \mathsf{distance} = A \cdot \bigl[\ B + f\left(\alpha + n\ \beta \right)\ \bigr]\ \bigl(\ 1.7275\ \bigr)^n ~. }[/math]
Note in particular that in Blagg's formula, the law for the Solar system was best represented by a progression in 1.7275, rather than the original value 2 used by Titius, Bode, and others.
Blagg examined the satellite system of Jupiter, Saturn, and Uranus, and discovered the same progression ratio 1.7275, in each.
However, the final form of the correction function f was not given in Blagg's 1913 paper, with Blagg noting that the empirical figures given were only for illustration. The empirical form was provided in the form of a graph (the reason that points on the curve are such a close match for empirical data, for objects discovered prior to 1913, is that they are the empirical data).
Finding a formula that closely fit the empircal curve turned out to be difficult. Fourier analysis of the shape resulted in the following seven term approximation:[14]
- [math]\displaystyle{ \ f \bigl(\ \theta\ \bigr) \;=\; 0.4594 \;+\; 0.396\ \cos\!\bigl(\ \theta - 27.4^{\circ}\ \bigr) \;+\; 0.168\ \cos\!\bigl(\ 2\ (\ \theta - 60.4^{\circ})\ \bigr) \;+\; 0.062\ \cos\!\bigl(\ 3\ (\ \theta - 28.1^{\circ})\ \bigr) \;+\; 0.053\ \cos\!\bigl(\ 4\ (\ \theta - 77.2^{\circ})\ \bigr) \;+\; 0.009\ \cos\!\bigl(\ 5\ (\ \theta - 22^{\circ})\ \bigr) \;+\; 0.012\ \cos\!\bigl(\ 7\ (\ \theta - 40.4^{\circ})\ \bigr) ~. }[/math]
After further analysis, Blagg gave the following simpler formula; however the price for the simpler form is that it produces a less accurate fit to the empirical data. Blagg gave it in an un-normalized form in her paper, which leaves the relative sizes of A, B, and f ambiguous; it is shown here in normalized form (i.e. this version of f is scaled to produce values ranging from 0 to 1, inclusive):[15]
- [math]\displaystyle{ \ f \bigl(\ \theta\ \bigr) \;=\; 0.249 \;+\; 0.860 \ \left( \frac{\ \cos\ \Psi\ }{\ 3 - \cos\!\left(\ 2 \Psi\ \right)\ } \;+\; \frac{ 1 }{\ 6 - 4\ \cos\!\left(\ 2\ \Psi - 60^{\circ} \right)\ } \right)\ , }[/math]
where [math]\displaystyle{ \ \Psi \equiv \theta - 27.5^{\circ} ~. }[/math]
Neither of these formulas for function f are used in the calculations below: The calculations here are based on a graph of function f which was drawn based on observed data.
Constants for Blagg's refinement of the Titius–Bode law
(as modified by Nieto 1970)System A B α β Sun-orbiting bodies 0.4162 2.025 112.4° 56.6° Moons of Jupiter 0.4523 1.852 113.0° 36.0° Moons of Saturn 3.074 0.0071 118.0° 10.0° Moons of Uranus 2.98 0.0805 125.7° 12.5°
Her paper was pulished in 1913, and was forgotten until 1953, when A.E. Roy came across it while researching another problem.[16] Roy noted that Blagg herself had suggested that her formula could give approximate mean distances of other bodies still undiscovered in 1913. Since then, six bodies in three systems examined by Blagg had been discovered: Pluto, Sinope (Jupiter IX), Lysithea (J X), Carme (J XI), Ananke (J XII), and Miranda (Uranus V).
Roy found that all six fitted very closely. This might have been an exaggeration: out of these six bodies, four were sharing positions with objects that were already known in 1913; concerning the two others, there was a ~6% overestimate for Pluto; and later, a 6% underestimate for Miranda became apparent.[15]
Another of Blagg's predictions was confirmed: That some bodies were preferentially clustered around particular distances.
Her formula also predicted that if a trans-plutonian planet existed, it would be at ~68 AU from the Sun. This prediction turned out to be extremely close to the measured semi-major axis of the dwarf planet, Eris.
Comparison of the Blagg formulation with observation
Bodies in parentheses were not known in 1913, when Blagg wrote her paper. Some of the calculated distances in the Saturn and Uranus systems are not very accurate. This is because the low values of constant B in the table above make them very sensitive to the exact form of the function f .
|
|
|
|
Richardson formulation
In a 1945 magazine article,[17] the science writer D.E. Richardson apparently independently arrived at the same conclusion as Blagg: That the progression ratio is 1.728 rather than 2. His spacing law is in the form:
- [math]\displaystyle{ \ R_{n} = \bigl(\ 1.728\ \bigr)^n\ \varrho_n ( \theta_n )\ , }[/math]
where [math]\displaystyle{ \ \varrho_n\ }[/math] is an oscillatory function with period [math]\displaystyle{ \ 2\ \pi\ , }[/math] representing distances [math]\displaystyle{ \ \varrho_n\ }[/math] from an off-centered origin to points on an ellipse.
Historical inertia
Nieto, who conducted the first modern comprehensive review of the Titius–Bode Law,[18] noted that "The psychological hold of the Law on astronomy has been such that people have always tended to regard its original form as the one on which to base theories." He was emphatic that "future theories must rid themselves of the bias of trying to explain a progression ratio of 2":
One thing which needs to be emphasized is that the historical bias towards a progression ratio of 2 must be abandoned. It ought to be clear that the first formulation of Titius (with its asymmetric first term) should be viewed as a good first guess. Certainly, it should not necessarily be viewed as the best guess to refer theories to. But in astronomy the weight of history is heavy ... Despite the fact that the number 1.73 is much better, astronomers cling to the original number 2.[1]
Theoretical explanations
No solid theoretical explanation underlies the Titius–Bode law – but it is possible that, given a combination of orbital resonance and shortage of degrees of freedom, any stable planetary system has a high probability of satisfying a Titius–Bode-type relationship. Since it may be a mathematical coincidence rather than a "law of nature", it is sometimes referred to as a rule instead of "law".[19] Astrophysicist Alan Boss states that it is just a coincidence, and the planetary science journal Icarus no longer accepts papers attempting to provide improved versions of the "law".[13]
Orbital resonance from major orbiting bodies creates regions around the Sun that are free of long-term stable orbits. Results from simulations of planetary formation support the idea that a randomly chosen, stable planetary system will likely satisfy a Titius–Bode law.[20]
Dubrulle and Graner[21][22] showed that power-law distance rules can be a consequence of collapsing-cloud models of planetary systems possessing two symmetries: rotational invariance (i.e., the cloud and its contents are axially symmetric) and scale invariance (i.e., the cloud and its contents look the same on all scales). The latter is a feature of many phenomena considered to play a role in planetary formation, such as turbulence.
Natural satellite systems and exoplanetary systems
Only a limited number of systems are available upon which Bode's law can presently be tested; two solar planets have enough large moons, that probably formed in a process similar to that which formed the planets: The four large satellites of Jupiter and the biggest inner satellite (i.e., Amalthea) cling to a regular, but non-Titius-Bode, spacing, with the four innermost satellites locked into orbital periods that are each twice that of the next inner satellite. Similarly, the large moons of Uranus have a regular but non-Titius-Bode spacing.[23] However, according to Martin Harwit
- "a slight new phrasing of this law permits us to include not only planetary orbits around the Sun, but also the orbits of moons around their parent planets."[24]
The new phrasing is known as “Dermott's law”.
Of the recent discoveries of extrasolar planetary systems, few have enough known planets to test whether similar rules apply. An attempt with 55 Cancri suggested the equation
- [math]\displaystyle{ ~ a_n = 0.0142 \cdot \mathrm{e}^{\left(\,0.9975\, n\,\right)} = 0.0142 \cdot \bigl(\, 2.7115 \,\bigr)^n ~, }[/math]
and controversially[25] predicts an undiscovered planet or asteroid field for [math]\displaystyle{ ~ n = 5 ~ }[/math] at 2 AU.[26] Furthermore, the orbital period and semi-major axis of the innermost planet in the 55 Cancri system have been greatly revised (from 2.817 days to 0.737 days and from 0.038 AU to 0.016 AU, respectively) since the publication of these studies.[27]
Recent astronomical research suggests that planetary systems around some other stars may follow Titius-Bode-like laws.[28][29] Bovaird & Lineweaver (2013)[30] applied a generalized Titius-Bode relation to 68 exoplanet systems that contain four or more planets. They showed that 96% of these exoplanet systems adhere to a generalized Titius-Bode relation to a similar or greater extent than the Solar System does. The locations of potentially undetected exoplanets are predicted in each system.[30]
Subsequent research detected 5 candidate planets from the 97 planets predicted for the 68 planetary systems. The study showed that the actual number of planets could be larger. The occurrence rates of Mars- and Mercury-sized planets are currently unknown, so many planets could be missed due to their small size. Other possible reasons that may account for apparent discrepancies include planets that do not transit the star or circumstances in which the predicted space is occupied by circumstellar disks. Despite these types of allowances, the number of planets found with Titius-Bode law predictions was lower than expected.[31]
In a 2018 paper, the idea of a hypothetical eighth planet around TRAPPIST-1 named "TRAPPIST‑1i", was proposed by using the Titius-Bode law. TRAPPIST‑1i had a prediction based exclusively on the Titius-Bode law with an orbital period of 27.53 ± 0.83 days.[32]
Finally, raw statistics from exoplanetary orbits strongly point to a general fulfillment of Titius-Bode-like laws (with exponential increase of semi-major axes as a function of planetary index) in all the exoplanetary systems; when making a blind histogram of orbital semi-major axes for all the known exoplanets for which this magnitude is known, and comparing it with what should be expected if planets distribute according to Titius-Bode-like laws, a significant degree of agreement (i.e., 78%)[33] is obtained.[34]
See also
- Dermott's law
- Phaeton (hypothetical planet)
- Logarithmic spiral
- Lennard-Jones potential
- Mysterium Cosmographicum
Footnotes
- ↑ The spacing seems to transition from the complicated Titius–series to simple equal-spacing starting at Saturn, with Neptune being the first major planet that does not fit the Titius–Bode rule.
- ↑ Bode's footnote was initially unsourced, but in later versions credited to Titius, and in Bode’s memoir he refers to Titius, clearly recognizing Titius' priority.
- ↑ The cossists were experts in calculations of all kinds and were employed by merchants and businessmen to solve complex accounting problems. Their name derives from the Italian word cosa, meaning "thing", because they used symbols to represent an unknown quantity, similar to the way modern mathematicians use [math]\displaystyle{ \,x\;. }[/math] Professional problem-solvers of this era invented their own clever methods for performing calculations and would do their utmost to keep these methods secret in order to maintain a reputation as the only person capable of solving a particular problem.[citation needed]
References
- ↑ 1.0 1.1 1.2 Nieto, Michael Martin (1970). "Conclusions about the Titius–Bode Law of Planetary Distances". Astron. Astrophys. 8: 105–111. Bibcode: 1970A&A.....8..105N.
- ↑ 2.0 2.1 Gregory, D. (1715). The Elements of Astronomy.
- ↑ 3.0 3.1 3.2 "Where should the planets be? The law of proportionalities". http://dawn.jpl.nasa.gov/mission/background_02.asp.
- ↑ 4.0 4.1 Bonnet, C. (1764). Contemplation de la Nature.
- ↑ Bode, Johann Elert (1772). Anleitung zur Kenntniss des gestirnten Himmels (2nd ed.).
- ↑ 6.0 6.1 Hoskin, Michael (1992-06-26). "Bodes' law and the discovery of Ceres". Observatorio Astronomico di Palermo "Giuseppe S. Vaiana". http://www.astropa.unipa.it/HISTORY/hoskin.html.
- ↑ von Wolf, C.F. (1723). Vernünftige Gedanken von den Wirkungen der Natur.
- ↑ Gregory, David (1702). Astronomiae physicae et geometricae elementa.
- ↑ Martin, Benjamin (1747). Philosophia Britannica.
- ↑ Cerdà, Tomàs (c. 1760). Tratado de Astronomía.
- ↑ Wurm, Vikarius (Johann Friedrich) (1787). Bode, J.E.. ed. "Verschiedene astronomische Bemerkungen und eine Abhandlung über mögliche Planeten und Kometen unsers Sonnensystems". Astronomisches Jahrbuch (Hofbuchdrucker, Berlin: George Jacob Decker, Königl) 15: 162–73.
- ↑ Peirce, C.S.; Ketner, Kenneth Laine (1992). Reasoning and the logic of things. The Cambridge conferences lectures of 1898. Harvard University Press. pp. 194–196. ISBN 978-0-674-74966-5. https://books.google.com/books?id=zdUkAQAAIAA&pg=PA194J. HUP catalog page.
- ↑ 13.0 13.1 Boss, Alan (October 2006). "Ask Astro". Astronomy 30 (10): 70.
- ↑ 14.0 14.1 "On a suggested substitute for Bode's law". Monthly Notices of the Royal Astronomical Society 73: 414–22. 1913. doi:10.1093/mnras/73.6.414.
- ↑ 15.0 15.1 Lobban, G.G. (October 1982). "A review of Blagg's formula in the light of recently discovered planetary moons and rings". Journal of the British Astronomical Association 92 (6): 260–263. Bibcode: 1982JBAA...92..260L. https://ui.adsabs.harvard.edu/link_gateway/1982JBAA...92..260L/ADS_PDF.
- ↑ Malcolm, Roy (1955). "Is Bode's law a coincidence?". Astounding Science Fiction LV (5).
- ↑ Richardson, D.E. (1945). "Distances of planets from the Sun and of satellites from their primaries in the satellite systems of Jupiter, Saturn, and Uranus". Popular Astronomy 53: 14–26.
- ↑ Nieto, Michael Martin (1972). The Titius–Bode Law of Planetary Distances – Its History and Theory (1st ed.). Pergamon Press. doi:10.1016/C2013-0-02478-4. ISBN 978-0-08-016784-8. https://www.elsevier.com/books/the-titius-bode-law-of-planetary-distances/9780080167848.
- ↑ Carroll, Bradley W.; Ostlie, Dale A. (2007). An Introduction to Modern Astrophysics. Pearson Addison-Wesley. pp. 716–717. ISBN 978-0-8053-0402-2. https://books.google.com/books?id=M8wPAQAAMAAJ&pg=PA716.
- ↑ Wayne Hayes; Scott Tremaine (October 1998). "Fitting selected random planetary systems to Titius–Bode laws". Icarus 135 (2): 549. doi:10.1006/icar.1998.5999. Bibcode: 1998Icar..135..549H. https://www.cs.toronto.edu/~wayne/research/papers/bode.pdf.
- ↑ F. Graner; B. Dubrulle (1994). "Titius–Bode laws in the solar system. Part I: Scale invariance explains everything". Astronomy and Astrophysics 282 (1): 262–268. Bibcode: 1994A&A...282..262G.
- ↑ B. Dubrulle; F. Graner (1994). "Titius–Bode laws in the solar system. Part II: Build your own law from disk models". Astronomy and Astrophysics 282 (1): 269–276. Bibcode: 1994A&A...282..269D.
- ↑ Cohen, Howard L. (May 1996). "The Titius-Bode relation revisited". FirstLight (Gainesville, FL: Alachua Astronomy Club). http://www.floridastars.org/9605cohe.html. Retrieved 2008-02-24.
- ↑ Harwit, Martin (1998). Astrophysical Concepts. Springer. pp. 27–29. ISBN 9780387949437. https://books.google.com/books?id=trAAgqWZVlkC&dq=%22origin+of+commensurabilities+in+the+solar+system%22&pg=PA614.
- ↑ Kotliarov, Ivan (21 June 2008). "The Titius-Bode law revisited but not revived". arXiv:0806.3532 [physics.space-ph].
- ↑ Poveda, Arcadio; Lara, Patricia (2008). "The exo-planetary system of 55 Cancri and the Titus–Bode law". Revista Mexicana de Astronomía y Astrofísica (44): 243–246. http://www.astroscu.unam.mx/rmaa/RMxAA..44-1/PDF/RMxAA..44-1_apoveda.pdf.
- ↑ Dawson, Rebekah I.; Fabrycky, Daniel C. (2010). "Radial velocity planets de-aliased. A new, short period for super-Earth 55 Cnc e". Astrophysical Journal 722 (1): 937–953. doi:10.1088/0004-637X/722/1/937. Bibcode: 2010ApJ...722..937D.
- ↑ "Section 8.2: Extrasolar Titius-Bode-like laws?" (PDF). European Southern Observatory (ESO.org) (Press release). The HARPS search for southern extra-solar planets. 2010-08-23. Retrieved 2010-08-24.
- ↑ Lara, Patricia (2012). "On the structural law of exoplanetary systems". ICNAAM 2012: International Conference of Numerical Analysis and Applied Mathematics. 1479. pp. 2356–2359. doi:10.1063/1.4756667. Bibcode: 2012AIPC.1479.2356L.
- ↑ 30.0 30.1 Bovaird, Timothy; Lineweaver, Charles H. (2013). "Exoplanet predictions based on the generalized Titius-Bode relation". Monthly Notices of the Royal Astronomical Society 435 (2): 1126. doi:10.1093/mnras/stt1357. Bibcode: 2013MNRAS.435.1126B.
- ↑ Huang, Chelsea X.; Bakos, Gáspár Á. (2014-05-09). "Testing the Titius-Bode law predictions for Kepler multi-planet systems". Monthly Notices of the Royal Astronomical Society 442 (1): 674–681. doi:10.1093/mnras/stu906. Bibcode: 2014MNRAS.442..674H.
- ↑ Kipping, David (2018). "Predicting the orbit of TRAPPIST-1i". Research Notes of the American Astronomical Society 2 (3): 136. doi:10.3847/2515-5172/aad6e8. Bibcode: 2018RNAAS...2..136K.
- ↑ Lara, Patricia; Cordero-Tercero, Guadalupe (2020). "The reliability of the Titius-Bode relation and its implications for the search for exoplanets". Publications of the Astronomical Society of Japan 72 (2). doi:10.1093/pasj/psz146.
- ↑ Ballesteros, F.J.; Fernandez-Soto, A.; Martinez, V.J. (2019). "Diving into exoplanets: Are water seas the most common?". Astrobiology 19 (5): 642–654. doi:10.1089/ast.2017.1720. PMID 30789285. Bibcode: 2019AsBio..19..642B.
Further reading
- Matthews, Robert (9 April 1994). "The ghostly hand that spaced the planets". New Scientist: 13. https://www.newscientist.com/article/mg14219202.300-science-the-ghostly-hand-that-spaced-the-planets-.html.
- Perdijk, H.J.R.. "The law of Titius–Bode explained". http://home.kpn.nl/oudfit/pp2/home.htm. — mystical & speculative; ref. diagrams missing from archive
- Parés i Farràs, Ramon, Dr. (2016). Distancias planetarias y ley de Titius-Bode (popular astronomy essay). http://media.wix.com/ugd/61b5e4_d5cf415763b44680806a8431ba375db2.pdf. Retrieved 2024-01-26. — combination history of distance measurements and development of Titius' law, notable astronomers involved, and exposition by graphs & simple ratios of modern planetary & satellite distances
 |