BCPNN
A Bayesian Confidence Propagation Neural Network (BCPNN) is an artificial neural network inspired by Bayes' theorem, which regards neural computation and processing as probabilistic inference. Neural unit activations represent probability ("confidence") in the presence of input features or categories, synaptic weights are based on estimated correlations and the spread of activation corresponds to calculating posterior probabilities. It was originally proposed by Anders Lansner and Örjan Ekeberg at KTH Royal Institute of Technology.[1] This probabilistic neural network model can also be run in generative mode to produce spontaneous activations and temporal sequences.
The basic model is a feedforward neural network comprising neural units with continuous activation, having a bias representing prior, and being connected by Bayesian weights in the form of point-wise mutual information. The original network has been extended to a modular structure of minicolumns and hypercolumns, representing discrete coded features or attributes.[2][3] The units can also be connected as a recurrent neural network (losing the strict interpretation of their activations as probabilities)[4] but becoming a possible abstract model of biological neural networks and associative memory.[5][6][7][8][9]
BCPNN has been used for machine learning classification[10] and data mining, for example for discovery of adverse drug reactions.[11] The BCPNN learning rule has also been used to model biological synaptic plasticity and intrinsic excitability in large-scale spiking neural network (SNN) models of cortical associative memory[12][13] and reward learning in Basal ganglia.[14]
Network architecture
The BCPNN network architecture is modular in terms of hypercolumns and minicolumns. This modular structure is inspired by and generalized from the modular structure of the mammalian cortex. In abstract models, the minicolumns serve as the smallest units and they typically feature a membrane time constant and adaptation. In spiking models of cortex, a layer 2/3 minicolumn is typically represented by some 30 pyramidal cells and one double bouquet cell.[15] The latter turns the negative BCPNN-weights formed between neurons with anti-correlated activity into di-synaptic inhibition.
Lateral inhibition within the hypercolumn makes it a soft winner-take-all module. Looking at real cortex, the number of minicolumns within a hypercolumn is on the order of a hundred, which makes the activity sparse, at the level of 1% or less, given that hypercolumns can also be silent.[16] A BCPNN network with a size of the human neocortex would have a couple of million hypercolumns, partitioned into some hundred areas. In addition to sparse activity, a large-scale BCPNN would also have very sparse connectivity, given that the real cortex is sparsely connected at the level of 0.01 - 0.001% on average.
Bayesian-Hebbian learning rule
The BCPNN learning rule was derived from Bayes rule and is Hebbian such that neural units with activity correlated over time get excitatory connections between them whereas anti-correlation generates inhibition and lack of correlation gives zero connections. The independence assumptions are the same as in naïve Bayes formalism. BCPNN represents a straight-forward way of deriving a neural network from Bayes rule.[2][3][17] In order to allow the use the standard equation for propagating activity between neurons, transformation to log space was necessary. The basic equations for postsynaptic unit intrinsic excitability and synaptic weight between pre- and postsynaptic units, , are:
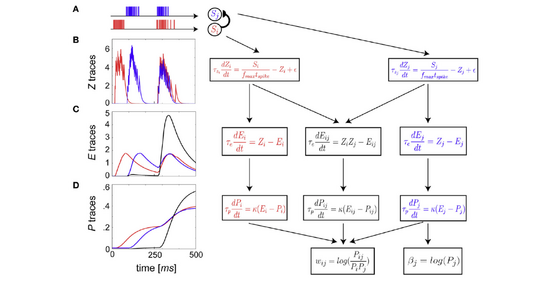
where the activation and co-activation probabilities are estimated from the training set, which can be done e.g. by exponentially weighted moving averages (see Figure).
There has been proposals for a biological interpretation of the BCPNN learning rule. may represent binding of glutamate to NMDA receptors, whereas could represent a back-propagating action potential reaching the synapse. The conjunction of these events lead to influx via NMDA channels, CaMKII activation, AMPA channel phosphorylation, and eventually enhanced synaptic conductance.
The traces are further filtered into the traces, which serve as temporal buffers, eligibility traces or synaptic tags necessary to allow delayed reward to affect synaptic parameters. E traces are subsequently filtered into the P traces that finally determine the values of bias and weight values. This summarizes many complex protein and non-protein dependent synaptic processes behind LTP, exhibiting highly variable timescales, from several seconds up to potentially days or months. The parameter κ ∈ [0, ∞] regulates the degree of plasticity or learning rate and is supposed to represent the release and action of some endogenous neuromodulator, e.g., dopamine activating D1R-like receptors, triggered by some unexpected emotionally salient situation, and resulting in neuromodulated activity dependent plasticity and learning.
Models of brain systems and functions
The cortex inspired modular architecture of BCPNN has been the basis for several spiking neural network models of cortex aimed at studying its associative memory functions. In these models, minicolumns comprise about 30 model pyramidal cells and a hypercolumn comprises ten or more such minicolumns and a population of basket cells that mediate local feedback inhibition. A modelled network is composed of about ten or more such hypercolumns. Connectivity is excitatory within minicolumns and support feedback inhibition between minicolumns in the same hypercolumn via model basket cells. Long-range connectivity between hypercolumns is sparse and excitatory and is typically set up to form number of distributed cell assemblies representing earlier encoded memories. Neuron and synapse properties have been tuned to represent their real counterparts in terms of e.g. spike frequency adaptation and fast non-Hebbian synaptic plasticity.
These cortical models have mainly been used to provide a better understanding of the mechanisms underlying cortical dynamics and oscillatory structure associated with different activity states.[18] Cortical oscillations in the range from theta, over alpha and beta to gamma are generated by this model. The embedded memories can be recalled from partial input and when activated they show signs of fixpoint attractor dynamics, though neural adaptation and synaptic depression terminates activity within some hundred milliseconds. Notably, a few cycles of gamma oscillations are generated during such a brief memory recall. Cognitive phenomena like attentional blink and its modulation by benzodiazepine has also been replicated in this model.[19]
In recent years, Hebbian plasticity has been incorporated into this cortex model and simulated with abstract non-spiking as well as spiking neural units.[17] This made it possible to demonstrate online learning of temporal sequences[20] as well as one-shot encoding and immediate recall in human word list learning.[12] These findings further lead to the proposal and investigation of a novel theory of working memory based on fast Hebbian synaptic plasticity.[13]
A similar approach was applied to model reward learning and behavior selection in a Go-NoGo connected non-spiking and spiking neural network models of the Basal ganglia.[14][21]
Machine learning applications
The point-wise mutual information weights of BCPNN is since long one of the standard methods for detection of drug adverse reactions.[11]
BCPNN has recently been successfully applied to Machine Learning classification benchmarks, most notably the hand written digits of the MNIST database. The BCPNN approach uses biologically plausible learning and structural plasticity for unsupervised generation of a sparse hidden representation, followed by a one-layer classifier that associates this representation to the output layer.[10] It achieves a classification performance on the full MNIST test set around 98%, comparable to other methods based on unsupervised representation learning.[22] The performance is notably slightly lower than that of the best methods that employ end-to-end error back-propagation. However, the extreme performance comes with a cost of lower biological plausibility and higher complexity of the learning machinery. The BCPNN method is also quite well suited for semi-supervised learning.
Hardware designs for BCPNN
The structure of BCPNN with its cortex-like modular architecture and massively parallel correlation based Hebbian learning makes it quite hardware friendly. Implementation with reduced number of bits in synaptic state variables have been shown to be feasible.[23] BCPNN has further been the target for parallel simulators on cluster computers and GPU:s. It was recently implemented on the SpiNNaker compute platform[24] as well as in a series of dedicated neuromorphic VLSI designs.[25][26][27][28] From these it has been estimated that a human cortex sized BCPNN with continuous learning could be executed in real time with a power dissipation on the order of few kW.
References
- ↑ "A one-layer feedback artificial neural network with a Bayesian learning rule". International Journal of Neural Systems 1 (1): 77–87. 1989. doi:10.1142/S0129065789000499.
- ↑ 2.0 2.1 "A higher order Bayesian neural network with spiking units". International Journal of Neural Systems 7 (2): 115–28. May 1996. doi:10.1142/S0129065796000816. PMID 8823623.
- ↑ 3.0 3.1 "A Bayesian attractor network with incremental learning". Network 13 (2): 179–94. May 2002. doi:10.1080/net.13.2.179.194. PMID 12061419.
- ↑ "Artificial Neural Networks. Proceedings of the 1991 International Conference on Artificial Neural Networks (ICANN-91)". 1–2. Espoo, Finland: Elsevier. June 1991.
- ↑ Lansner, Anders (1986). INVESTIGATIONS INTO THE PATIERN PROCESSING CAPABILITIES OF ASSOCIATIVE NETS. KTH Royal Institute of Technology. http://urn.kb.se/resolve?urn=urn:nbn:se:kth:diva-292426.
- ↑ "A model of cortical associative memory based on a horizontal network of connected columns". Network: Computation in Neural Systems 9 (2): 235–264. January 1998. doi:10.1088/0954-898x_9_2_006. ISSN 0954-898X. PMID 9861988.
- ↑ "Modelling Hebbian cell assemblies comprised of cortical neurons". Network: Computation in Neural Systems 3 (2): 105–119. January 1992. doi:10.1088/0954-898x_3_2_002. ISSN 0954-898X.
- ↑ "Associative memory models: from the cell-assembly theory to biophysically detailed cortex simulations". Trends in Neurosciences 32 (3): 178–86. March 2009. doi:10.1016/j.tins.2008.12.002. PMID 19187979.
- ↑ "Theta and gamma power increases and alpha/beta power decreases with memory load in an attractor network model". Journal of Cognitive Neuroscience 23 (10): 3008–20. October 2011. doi:10.1162/jocn_a_00029. PMID 21452933.
- ↑ 10.0 10.1 "Learning representations in Bayesian Confidence Propagation neural networks". 2020 International Joint Conference on Neural Networks (IJCNN). IEEE. 2020. pp. 1–7. doi:10.1109/IJCNN48605.2020.9207061. ISBN 978-1-7281-6926-2.
- ↑ 11.0 11.1 "Bayesian neural networks with confidence estimations applied to data mining". Computational Statistics & Data Analysis 34 (4): 473–493. 2000. doi:10.1016/S0167-9473(99)00114-0.
- ↑ 12.0 12.1 "A Spiking Working Memory Model Based on Hebbian Short-Term Potentiation". The Journal of Neuroscience 37 (1): 83–96. January 2017. doi:10.1523/JNEUROSCI.1989-16.2016. PMID 28053032.
- ↑ 13.0 13.1 "An Indexing Theory for Working Memory Based on Fast Hebbian Plasticity". eNeuro 7 (2): ENEURO.0374–19.2020. March 2020. doi:10.1523/ENEURO.0374-19.2020. PMID 32127347.
- ↑ 14.0 14.1 "Action selection performance of a reconfigurable basal ganglia inspired model with Hebbian-Bayesian Go-NoGo connectivity" (in English). Frontiers in Behavioral Neuroscience 6: 65. 2012. doi:10.3389/fnbeh.2012.00065. PMID 23060764.
- ↑ "Introducing double bouquet cells into a modular cortical associative memory model". Journal of Computational Neuroscience 47 (2–3): 223–230. December 2019. doi:10.1007/s10827-019-00729-1. PMID 31502234.
- ↑ "A modular attractor associative memory with patchy connectivity and weight pruning". Network: Computation in Neural Systems 24 (4): 129–50. December 2013. doi:10.3109/0954898X.2013.859323. PMID 24251411. http://urn.kb.se/resolve?urn=urn:nbn:se:kth:diva-124654.
- ↑ 17.0 17.1 "Synaptic and nonsynaptic plasticity approximating probabilistic inference". Frontiers in Synaptic Neuroscience 6: 8. April 2014. doi:10.3389/fnsyn.2014.00008. PMID 24782758.
- ↑ "Bistable, irregular firing and population oscillations in a modular attractor memory network". PLOS Computational Biology 6 (6). June 2010. doi:10.1371/journal.pcbi.1000803. PMID 20532199. Bibcode: 2010PLSCB...6E0803L.
- ↑ "Is attentional blink a byproduct of neocortical attractors?". Frontiers in Computational Neuroscience 5: 13. 2011. doi:10.3389/fncom.2011.00013. PMID 21625630.
- ↑ "Spike-Based Bayesian-Hebbian Learning of Temporal Sequences". PLOS Computational Biology 12 (5). May 2016. doi:10.1371/journal.pcbi.1004954. PMID 27213810. Bibcode: 2016PLSCB..12E4954T.
- ↑ "Functional Relevance of Different Basal Ganglia Pathways Investigated in a Spiking Model with Reward Dependent Plasticity". Frontiers in Neural Circuits 10: 53. July 2016. doi:10.3389/fncir.2016.00053. PMID 27493625.
- ↑ Ravichandran NB, Lansner A, Herman P (May 2020). "Brain-like approaches to unsupervised learning of hidden representations--a comparative study". arXiv:2005.03476 [cs.NE].
- ↑ "Reducing the computational footprint for real-time BCPNN learning". Frontiers in Neuroscience 9: 2. January 2015. doi:10.3389/fnins.2015.00002. PMID 25657618.
- ↑ "Large-Scale Simulations of Plastic Neural Networks on Neuromorphic Hardware". Frontiers in Neuroanatomy 10: 37. April 2016. doi:10.3389/fnana.2016.00037. PMID 27092061.
- ↑ "A scalable custom simulation machine for the Bayesian Confidence Propagation Neural Network model of the brain". 2014 19th Asia and South Pacific Design Automation Conference (ASP-DAC). Singapore: IEEE. January 2014. pp. 578–585. doi:10.1109/ASPDAC.2014.6742953. ISBN 978-1-4799-2816-3.
- ↑ "Spiking brain models: Computation, memory and communication constraints for custom hardware implementation". 2014 19th Asia and South Pacific Design Automation Conference (ASP-DAC). Singapore: IEEE. January 2014. pp. 556–562. doi:10.1109/ASPDAC.2014.6742950. ISBN 978-1-4799-2816-3.
- ↑ "eBrainII: a 3 kW Realtime Custom 3D DRAM Integrated ASIC Implementation of a Biologically Plausible Model of a Human Scale Cortex" (in en). Journal of Signal Processing Systems 92 (11): 1323–1343. November 2020. doi:10.1007/s11265-020-01562-x. ISSN 1939-8018. Bibcode: 2020JSPSy..92.1323S.
- ↑ "Optimizing BCPNN Learning Rule for Memory Access". Frontiers in Neuroscience 14. August 2020. doi:10.3389/fnins.2020.00878. PMID 32982673.
 |
