Balding–Nichols model

Short description: Model in population genetics

Balding-Nichols

Probability density function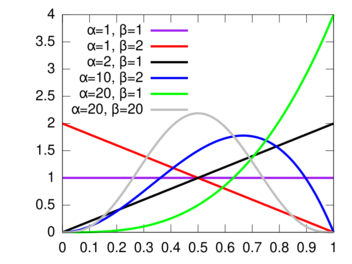
Cumulative distribution function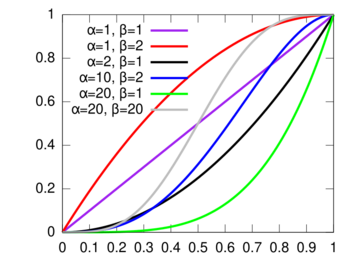
Parameters	[math]\displaystyle{ 0 \lt F \lt 1 }[/math](real) [math]\displaystyle{ 0\lt p \lt 1 }[/math] (real) For ease of notation, let [math]\displaystyle{ \alpha=\tfrac{1-F}{F}p }[/math], and [math]\displaystyle{ \beta=\tfrac{1-F}{F}(1-p) }[/math]
Support	[math]\displaystyle{ x \in (0; 1)\! }[/math]
PDF	[math]\displaystyle{ \frac{x^{\alpha-1}(1-x)^{\beta-1}} {\mathrm{B}(\alpha,\beta)}\! }[/math]
CDF	[math]\displaystyle{ I_x(\alpha,\beta)\! }[/math]
Mean	[math]\displaystyle{ p\! }[/math]
Median	[math]\displaystyle{ I_{0.5}^{-1}(\alpha,\beta) }[/math] no closed form
Mode	[math]\displaystyle{ \frac{F-(1-F)p}{3F-1} }[/math]
Variance	[math]\displaystyle{ Fp(1-p)\! }[/math]
Skewness	[math]\displaystyle{ \frac{2F(1-2p)}{(1+F)\sqrt{F(1-p)p}} }[/math]
MGF	[math]\displaystyle{ 1 +\sum_{k=1}^{\infty} \left( \prod_{r=0}^{k-1} \frac{\alpha+r}{\frac{1-F}{F}+r}\right) \frac{t^k}{k!} }[/math]
CF	[math]\displaystyle{ {}_1F_1(\alpha; \alpha+\beta; i\,t)\! }[/math]

In population genetics, the Balding–Nichols model is a statistical description of the allele frequencies in the components of a sub-divided population. With background allele frequency p the allele frequencies, in sub-populations separated by Wright's F_ST F, are distributed according to independent draws from

[math]\displaystyle{ B\left(\frac{1-F}{F}p,\frac{1-F}{F}(1-p)\right) }[/math]

where B is the Beta distribution. This distribution has mean p and variance Fp(1 – p).

The model is due to David Balding and Richard Nichols and is widely used in the forensic analysis of DNA profiles and in population models for genetic epidemiology.