Biology:Coefficient of inbreeding
The coefficient of inbreeding of an individual is the probability that two alleles at any locus in an individual are identical by descent from the common ancestor(s) of the two parents.[1][2][3][4]
Calculation
An individual is said to be inbred if there is a loop in its pedigree chart. A loop is defined as a path that runs from an individual up to the common ancestor through one parent and back down to the other parent, without going through any individual twice. The number of loops is always the number of common ancestors the parents have. If an individual is inbred, the coefficient of inbreeding is calculated by summing all the probabilities that an individual receives the same allele from its father's side and mother's side. As every individual has a 50% chance of passing on an allele to the next generation, the formula depends on 0.5 raised to the power of however many generations separate the individual from the common ancestor of its parents, on both the father's side and mother's side. This number of generations can be calculated by counting how many individuals lie in the loop defined earlier. Thus, the coefficient of inbreeding (f) of an individual X can be calculated with the following formula:[5]
[math]\displaystyle{ f_X = \sum 0.5^{n - 1} \cdot (1 + f_{A}) }[/math]
where [math]\displaystyle{ n }[/math] is the number of individuals in the aforementioned loop,
and [math]\displaystyle{ f_A }[/math] is the coefficient of inbreeding of the common ancestor of X's parents.
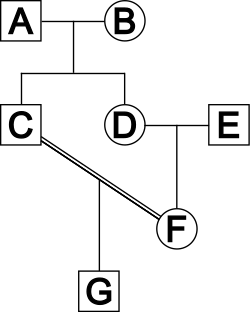
To give an example, consider the following pedigree.
In this pedigree chart, G is the progeny of C and F, and C is the biological uncle of F. To find the coefficient of inbreeding of G, first locate a loop that leads from G to the common ancestor through one parent and back down to the other parent without going through the same individual twice, There are only two such loops in this chart, as there are only 2 common ancestors of C and F. The loops are G - C - A - D - F and G - C - B - D - F, both of which have 5 members.
Because the common ancestors of the parents (A and B) are not inbred themselves, [math]\displaystyle{ f_A = 0 }[/math]. Therefore the coefficient of inbreeding of individual G is [math]\displaystyle{ f_G = \sum 0.5^{5 - 1} \cdot (1 + 0) = 0.5^{4} + 0.5^{4} = 12.5% }[/math].
If the parents of an individual are not inbred themselves, the coefficient of inbreeding of the individual is one-half the coefficient of relationship between the parents. This can be verified in the previous example, as 12.5% is one-half of 25%, the coefficient of relationship between an uncle and a niece.
Table of coefficients of inbreeding
| Generations | Coefficient of inbreeding (f) |
|---|---|
| 1 | 25% |
| 2 | 37.5% |
| 3 | 50% |
| 4 | 59.375% |
| 5 | 67.1875% |
| 6 | 73.4375% |
| 7 | 78.5156% |
| 8 | 82.6172% |
| 9 | 85.9375% |
| 10 | 88.623% |
| 11 | 90.7959% |
| 12 | 92.5537% |
| 13 | 93.9758% |
| 14 | 95.1263% |
| 15 | 96.0571% |
| 16 | 96.8102% |
| 17 | 97.4194% |
| 18 | 97.9122% |
| 19 | 98.3109% |
| 20 | 98.6335%[6] |
References
- ↑ Wright, Sewall (1922), "Coefficients of Inbreeding and Relationship", The American Naturalist 56: pp. 330–338
- ↑ Redei, George P. (2004), Encyclopedic Dictionary of Genetics, Genomics and Proteomics, John Wiley and Sons, Inc.
- ↑ Charlesworth, Deborah (2005), Inbreeding, John Wiley and Sons, Inc.
- ↑ Falconer, D.S.; Mackay, T.F.C. (1996), Introduction to Quantitative Genetics (4 ed.), Longman
- ↑ Schonewald-Cox, C.M., S.M. Chambers, B. MacBryde, and L. Thomas (eds.). 1983. Genetics and Conservation. Benjamin/Cummings, Menlo Park, Calif.
- ↑ At this point the individuals are considered to be part of an inbred strain, and each individual can effectively be considered to be clones.
 |