Bayesian inference in phylogeny
| Classification | Evolutionary biology |
|---|---|
| Subclassification | Molecular phylogenetics |
| Optimally search criteria | Bayesian inference |
Bayesian inference of phylogeny combines the information in the prior and in the data likelihood to create the so-called posterior probability of trees, which is the probability that the tree is correct given the data, the prior and the likelihood model. Bayesian inference was introduced into molecular phylogenetics in the 1990s by three independent groups: Bruce Rannala and Ziheng Yang in Berkeley,[1][2] Bob Mau in Madison,[3] and Shuying Li in University of Iowa,[4] the last two being PhD students at the time. The approach has become very popular since the release of the MrBayes software in 2001,[5] and is now one of the most popular methods in molecular phylogenetics.
Bayesian inference of phylogeny background and bases
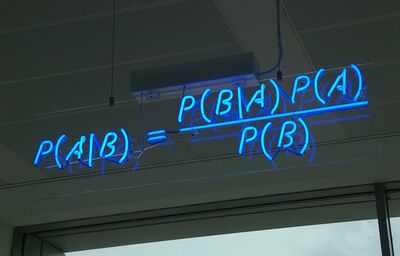
thumb|Metaphor illustrating MCMC method stepsBayesian inference refers to a probabilistic method developed by Reverend Thomas Bayes based on Bayes' theorem. Published posthumously in 1763 it was the first expression of inverse probability and the basis of Bayesian inference. Independently, unaware of Bayes' work, Pierre-Simon Laplace developed Bayes' theorem in 1774.[6]
Bayesian inference or the inverse probability method was the standard approach in statistical thinking until the early 1900s before RA Fisher developed what's now known as the classical/frequentist/Fisherian inference. Computational difficulties and philosophical objections had prevented the widespread adoption of the Bayesian approach until the 1990s, when Markov Chain Monte Carlo (MCMC) algorithms revolutionized Bayesian computation.
The Bayesian approach to phylogenetic reconstruction combines the prior probability of a tree P(A) with the likelihood of the data (B) to produce a posterior probability distribution on trees P(A|B).[7] The posterior probability of a tree will be the probability that the tree is correct, given the prior, the data, and the correctness of the likelihood model.
MCMC methods can be described in three steps: first using a stochastic mechanism a new state for the Markov chain is proposed. Secondly, the probability of this new state to be correct is calculated. Thirdly, a new random variable (0,1) is proposed. If this new value is less than the acceptance probability the new state is accepted and the state of the chain is updated. This process is run thousands or millions of times. The number of times a single tree is visited during the course of the chain is an approximation of its posterior probability. Some of the most common algorithms used in MCMC methods include the Metropolis–Hastings algorithms, the Metropolis-Coupling MCMC (MC³) and the LOCAL algorithm of Larget and Simon.
Metropolis–Hastings algorithm
One of the most common MCMC methods used is the Metropolis–Hastings algorithm,[8] a modified version of the original Metropolis algorithm.[9] It is a widely used method to sample randomly from complicated and multi-dimensional distribution probabilities. The Metropolis algorithm is described in the following steps:[10] [11]
- An initial tree, Ti, is randomly selected.
- A neighbour tree, Tj, is selected from the collection of trees.
- The ratio, R, of the probabilities (or probability density functions) of Tj and Ti is computed as follows: R = f(Tj)/f(Ti)
- If R ≥ 1, Tj is accepted as the current tree.
- If R < 1, Tj is accepted as the current tree with probability R, otherwise Ti is kept.
- At this point the process is repeated from Step 2 N times.
The algorithm keeps running until it reaches an equilibrium distribution. It also assumes that the probability of proposing a new tree Tj when we are at the old tree state Ti, is the same probability of proposing Ti when we are at Tj. When this is not the case Hastings corrections are applied. The aim of Metropolis-Hastings algorithm is to produce a collection of states with a determined distribution until the Markov process reaches a stationary distribution. The algorithm has two components:
- A potential transition from one state to another (i → j) using a transition probability function qi,j
- Movement of the chain to state j with probability αi,j and remains in i with probability 1 – αi,j.[2]
Metropolis-coupled MCMC
Metropolis-coupled MCMC algorithm (MC³) [12] has been proposed to solve a practical concern of the Markov chain moving across peaks when the target distribution has multiple local peaks, separated by low valleys, are known to exist in the tree space. This is the case during heuristic tree search under maximum parsimony (MP), maximum likelihood (ML), and minimum evolution (ME) criteria, and the same can be expected for stochastic tree search using MCMC. This problem will result in samples not approximating correctly to the posterior density. The (MC³) improves the mixing of Markov chains in presence of multiple local peaks in the posterior density. It runs multiple (m) chains in parallel, each for n iterations and with different stationary distributions , , where the first one, is the target density, while , are chosen to improve mixing. For example, one can choose incremental heating of the form:
so that the first chain is the cold chain with the correct target density, while chains are heated chains. Note that raising the density to the power with has the effect of flattening out the distribution, similar to heating a metal. In such a distribution, it is easier to traverse between peaks (separated by valleys) than in the original distribution. After each iteration, a swap of states between two randomly chosen chains is proposed through a Metropolis-type step. Let be the current state in chain , . A swap between the states of chains and is accepted with probability:
At the end of the run, output from only the cold chain is used, while those from the hot chains are discarded. Heuristically, the hot chains will visit the local peaks rather easily, and swapping states between chains will let the cold chain occasionally jump valleys, leading to better mixing. However, if is unstable, proposed swaps will seldom be accepted. This is the reason for using several chains which differ only incrementally.
An obvious disadvantage of the algorithm is that chains are run and only one chain is used for inference. For this reason, is ideally suited for implementation on parallel machines, since each chain will in general require the same amount of computation per iteration.
LOCAL algorithm of Larget and Simon
The LOCAL algorithms[13] offers a computational advantage over previous methods and demonstrates that a Bayesian approach is able to assess uncertainty computationally practical in larger trees. The LOCAL algorithm is an improvement of the GLOBAL algorithm presented in Mau, Newton and Larget (1999)[14] in which all branch lengths are changed in every cycle. The LOCAL algorithms modifies the tree by selecting an internal branch of the tree at random. The nodes at the ends of this branch are each connected to two other branches. One of each pair is chosen at random. Imagine taking these three selected edges and stringing them like a clothesline from left to right, where the direction (left/right) is also selected at random. The two endpoints of the first branch selected will have a sub-tree hanging like a piece of clothing strung to the line. The algorithm proceeds by multiplying the three selected branches by a common random amount, akin to stretching or shrinking the clothesline. Finally the leftmost of the two hanging sub-trees is disconnected and reattached to the clothesline at a location selected uniformly at random. This would be the candidate tree.
Suppose we began by selecting the internal branch with length that separates taxa and from the rest. Suppose also that we have (randomly) selected branches with lengths and from each side, and that we oriented these branches. Let , be the current length of the clothesline. We select the new length to be , where is a uniform random variable on . Then for the LOCAL algorithm, the acceptance probability can be computed to be:
Assessing convergence
To estimate a branch length of a 2-taxon tree under JC, in which sites are unvaried and are variable, assume exponential prior distribution with rate . The density is . The probabilities of the possible site patterns are:
for unvaried sites, and
Thus the unnormalized posterior distribution is:
or, alternately,
Update branch length by choosing new value uniformly at random from a window of half-width centered at the current value:
where is uniformly distributed between and . The acceptance probability is:
Example: , . We will compare results for two values of , and . In each case, we will begin with an initial length of and update the length times.
Maximum parsimony and maximum likelihood

thumb|200px|right|Example of long branch attraction. Longer branches (A & C) appear to be more closely related. There are many approaches to reconstructing phylogenetic trees, each with advantages and disadvantages, and there is no straightforward answer to “what is the best method?”. Maximum parsimony (MP) and maximum likelihood (ML) are traditional methods widely used for the estimation of phylogenies and both use character information directly, as Bayesian methods do.
Maximum Parsimony recovers one or more optimal trees based on a matrix of discrete characters for a certain group of taxa and it does not require a model of evolutionary change. MP gives the most simple explanation for a given set of data, reconstructing a phylogenetic tree that includes as few changes across the sequences as possible. The support of the tree branches is represented by bootstrap percentage. For the same reason that it has been widely used, its simplicity, MP has also received criticism and has been pushed into the background by ML and Bayesian methods. MP presents several problems and limitations. As shown by Felsenstein (1978), MP might be statistically inconsistent,[15] meaning that as more and more data (e.g. sequence length) is accumulated, results can converge on an incorrect tree and lead to long branch attraction, a phylogenetic phenomenon where taxa with long branches (numerous character state changes) tend to appear more closely related in the phylogeny than they really are. For morphological data, recent simulation studies suggest that parsimony may be less accurate than trees built using Bayesian approaches,[16] potentially due to overprecision,[17] although this has been disputed.[18] Studies using novel simulation methods have demonstrated that differences between inference methods result from the search strategy and consensus method employed, rather than the optimization used.[19]
As in maximum parsimony, maximum likelihood will evaluate alternative trees. However it considers the probability of each tree explaining the given data based on a model of evolution. In this case, the tree with the highest probability of explaining the data is chosen over the other ones.[20] In other words, it compares how different trees predict the observed data. The introduction of a model of evolution in ML analyses presents an advantage over MP as the probability of nucleotide substitutions and rates of these substitutions are taken into account, explaining the phylogenetic relationships of taxa in a more realistic way. An important consideration of this method is the branch length, which parsimony ignores, with changes being more likely to happen along long branches than short ones. This approach might eliminate long branch attraction and explain the greater consistency of ML over MP. Although considered by many to be the best approach to inferring phylogenies from a theoretical point of view, ML is computationally intensive and it is almost impossible to explore all trees as there are too many. Bayesian inference also incorporates a model of evolution and the main advantages over MP and ML are that it is computationally more efficient than traditional methods, it quantifies and addresses the source of uncertainty and is able to incorporate complex models of evolution.
Pitfalls and controversies
- Bootstrap values vs posterior probabilities. It has been observed that bootstrap support values, calculated under parsimony or maximum likelihood, tend to be lower than the posterior probabilities obtained by Bayesian inference.[21][22][23][24][25] This leads to a number of questions such as: Do posterior probabilities lead to overconfidence in the results?[26] Are bootstrap values more robust than posterior probabilities?
- Controversy of using prior probabilities. Using prior probabilities for Bayesian analysis has been seen by many as an advantage as it provides a way of incorporating information from sources other than the data being analyzed. However, when such external information is lacking, one is forced to use a prior even if it is impossible to use a statistical distribution to represent total ignorance. It is also a concern that the Bayesian posterior probabilities may reflect subjective opinions when the prior is arbitrary and subjective.
- Model choice. The results of the Bayesian analysis of a phylogeny are directly correlated to the model of evolution chosen so it is important to choose a model that fits the observed data, otherwise inferences in the phylogeny will be erroneous. Many scientists have raised questions about the interpretation of Bayesian inference when the model is unknown or incorrect. For example, an oversimplified model might give higher posterior probabilities.[21][27]
MrBayes software
MrBayes is a free software tool that performs Bayesian inference of phylogeny. It was originally written by John P. Huelsenbeck and Frederik Ronquist in 2001.[28] As Bayesian methods increased in popularity, MrBayes became one of the software of choice for many molecular phylogeneticists. It is offered for Macintosh, Windows, and UNIX operating systems and it has a command-line interface. The program uses the standard MCMC algorithm as well as the Metropolis coupled MCMC variant. MrBayes reads aligned matrices of sequences (DNA or amino acids) in the standard NEXUS format.[29]
MrBayes uses MCMC to approximate the posterior probabilities of trees.[9] The user can change assumptions of the substitution model, priors and the details of the MC³ analysis. It also allows the user to remove and add taxa and characters to the analysis. The program uses the most standard model of DNA substitution, the 4x4 also called JC69, which assumes that changes across nucleotides occur with equal probability.[30] It also implements a number of 20x20 models of amino acid substitution, and codon models of DNA substitution. It offers different methods for relaxing the assumption of equal substitutions rates across nucleotide sites.[31] MrBayes is also able to infer ancestral states accommodating uncertainty to the phylogenetic tree and model parameters.
MrBayes 3[32] was a completely reorganized and restructured version of the original MrBayes. The main novelty was the ability of the software to accommodate heterogeneity of data sets. This new framework allows the user to mix models and take advantages of the efficiency of Bayesian MCMC analysis when dealing with different type of data (e.g. protein, nucleotide, and morphological). It uses the Metropolis-Coupling MCMC by default.
MrBayes 3.2 was released in 2012[33] The new version allows the users to run multiple analyses in parallel. It also provides faster likelihood calculations and allow these calculations to be delegated to graphics processing unites (GPUs). Version 3.2 provides wider outputs options compatible with FigTree and other tree viewers.
List of phylogenetics software
This table includes some of the most common phylogenetic software used for inferring phylogenies under a Bayesian framework. Some of them do not use exclusively Bayesian methods.
| Name | Description | Method | Author | Website link |
|---|---|---|---|---|
| MrBayes | Phylogenetic inference | A program for Bayesian inference and model choice across a wide range of phylogenetic and evolutionary models. | Zangh, Huelsenbeck, Der Mark, Ronquist & Teslenko | https://nbisweden.github.io/MrBayes/ |
| BEAST | Bayesian Evolutionary Analysis Sampling Trees | Bayesian inference, relaxed molecular clock, demographic history | A. J. Drummond, A. Rambaut & M. A. Suchard [34] | https://beast.community |
| BEAST 2 | A software platform for Bayesian evolutionary analysis | Bayesian inference, packages, multiple models | R Bouckaert, J Heled, D Kühnert, T Vaughan, CH Wu, D Xie, MA Suchard, A Rambaut, AJ Drummond.[35] | http://www.beast2.org |
| PhyloBayes / PhyloBayes MPI | Bayesian Monte Carlo Markov Chain (MCMC) sampler for phylogenetic reconstruction. | Non-parametric methods for modeling among-site variation in nucleotide or amino-acid propensities. | N. Lartillot, N. Rodrigue, D. Stubbs, J. Richer [36] | http://www.atgc-montpellier.fr/phylobayes/ |
| Bali-Phy | Simultaneous Bayesian inference of alignment and phylogeny | Bayesian inference, alignment as well as tree search | Suchard MA, Redelings BD[37] | http://www.bali-phy.org |
| BUCKy | Bayesian concordance of gene trees | Bayesian concordance using modified greedy consensus of unrooted quartets | C. Ané, B. Larget, D.A. Baum, S.D. Smith, A. Rokas and B. Larget, S.K. Kotha, C.N. Dewey, C. Ané[38] | http://www.stat.wisc.edu/~ane/bucky/ |
| Bayes Phylogenies | Bayesian inference of trees using Markov Chain Monte Carlo methods | Bayesian inference, multiple models, mixture model (auto-partitioning) | M. Pagel, A. Meade[39] | http://www.evolution.rdg.ac.uk/BayesPhy.html |
| Armadillo Workflow Platform | Workflow platform dedicated to phylogenetic and general bioinformatic analysis | GUI wrapper around MrBayes | E. Lord, M. Leclercq, A. Boc, A.B. Diallo and V. Makarenkov[40] | https://github.com/armadilloUQAM/armadillo2/ |
| Geneious (MrBayes plugin) | Geneious provides genome and proteome research tools | GUI wrapper around MrBayes | A. J. Drummond,M.Suchard,V.Lefort et al. | http://www.geneious.com |
| TOPALi | Phylogenetic inference | GUI wrapper around MrBayes | I.Milne, D.Lindner, et al.[41] | http://www.topali.org |
Applications
Bayesian Inference has extensively been used by molecular phylogeneticists for a wide number of applications. Some of these include:

- Inference of phylogenies.[42][43]
- Inference and evaluation of uncertainty of phylogenies.[44]
- Inference of ancestral character state evolution.[45][46]
- Inference of ancestral areas.[47]
- Molecular dating analysis.[48][49]
- Model dynamics of species diversification and extinction[50]
- Elucidate patterns in pathogens dispersal.[51]
- Inference of phenotypic trait evolution.[52][53]
References
- ↑ Rannala, Bruce; Yang, Ziheng (September 1996). "Probability distribution of molecular evolutionary trees: A new method of phylogenetic inference". Journal of Molecular Evolution 43 (3): 304–311. doi:10.1007/BF02338839. PMID 8703097. Bibcode: 1996JMolE..43..304R.
- ↑ 2.0 2.1 Yang, Z.; Rannala, B. (1 July 1997). "Bayesian phylogenetic inference using DNA sequences: a Markov Chain Monte Carlo Method". Molecular Biology and Evolution 14 (7): 717–724. doi:10.1093/oxfordjournals.molbev.a025811. PMID 9214744.
- ↑ Mau, Bob; Newton, Michael A.; Larget, Bret (March 1999). "Bayesian Phylogenetic Inference via Markov Chain Monte Carlo Methods". Biometrics 55 (1): 1–12. doi:10.1111/j.0006-341x.1999.00001.x. PMID 11318142.
- ↑ Li, Shuying; Pearl, Dennis K.; Doss, Hani (June 2000). "Phylogenetic Tree Construction Using Markov Chain Monte Carlo". Journal of the American Statistical Association 95 (450): 493–508. doi:10.1080/01621459.2000.10474227. http://rave.ohiolink.edu/etdc/view?acc_num=osu1487942182323916.
- ↑ Huelsenbeck, J. P.; Ronquist, F. (1 August 2001). "MRBAYES: Bayesian inference of phylogenetic trees". Bioinformatics 17 (8): 754–755. doi:10.1093/bioinformatics/17.8.754. PMID 11524383.
- ↑ "Memoire sur la Probabilite des Causes par les Evenements". L'Académie Royale des Sciences 6: 621–656. 1774. NAID 10010866843. English translation by "Memoir on the Probability of the Causes of Events". Statistical Science 1 (3): 359–378. 1986. doi:10.1214/ss/1177013620.
- ↑ Nascimento, Fabrícia F.; Reis, Mario dos; Yang, Ziheng (October 2017). "A biologist's guide to Bayesian phylogenetic analysis". Nature Ecology & Evolution 1 (10): 1446–1454. doi:10.1038/s41559-017-0280-x. PMID 28983516. Bibcode: 2017NatEE...1.1446N.
- ↑ "Monte Carlo sampling methods using Markov chains and their applications". Biometrika 57 (1): 97–109. April 1970. doi:10.1093/biomet/57.1.97. Bibcode: 1970Bimka..57...97H.
- ↑ 9.0 9.1 "Equation of state calculations by fast computing machines". The Journal of Chemical Physics 21 (6): 1087–92. June 1953. doi:10.1063/1.1699114. Bibcode: 1953JChPh..21.1087M.
- ↑ Inferring phylogenies. Sunderland, Massachusetts: Sinauer Associates. 2004.
- ↑ Molecular Evolution: A Statistical Approach. Oxford, England: Oxford University Press. 2014.
- ↑ "Markov chain Monte Carlo maximum likelihood.". Computing Science and Statistics: Proceedings of the 23rd Symposium on the Interface.. Fairfax Station: Interface Foundation. 1991. pp. 156–163. OCLC 26603816.
- ↑ "Markov chain Monte Carlo algorithms for the Bayesian analysis of phylogenetic trees". Molecular Biology and Evolution 16 (6): 750–9. June 1999. doi:10.1093/oxfordjournals.molbev.a026160.
- ↑ "Bayesian phylogenetic inference via Markov chain Monte Carlo methods". Biometrics 55 (1): 1–12. March 1999. doi:10.1111/j.0006-341x.1999.00001.x. PMID 11318142.
- ↑ "Cases in which parsimony or compatibility methods will be positively misleading". Systematic Zoology 27 (4): 401–10. December 1978. doi:10.1093/sysbio/27.4.401.
- ↑ "Fluctuations in population fecundity drive variation in demographic connectivity and metapopulation dynamics". Proceedings. Biological Sciences 284 (1847): 20162086. January 2017. doi:10.1098/rspb.2016.2086. PMID 28123088.
- ↑ "Bayesian methods outperform parsimony but at the expense of precision in the estimation of phylogeny from discrete morphological data". Biology Letters 12 (4): 20160081. April 2016. doi:10.1098/rsbl.2016.0081. PMID 27095266.
- ↑ "Weighted parsimony outperforms other methods of phylogenetic inference under models appropriate for morphology". Cladistics 34 (4): 407–437. 2018. doi:10.1111/cla.12205. ISSN 0748-3007. PMID 34649370.
- ↑ "Morphological phylogenetics evaluated using novel evolutionary simulations". Systematic Biology 69 (5): 897–912. February 2020. doi:10.1093/sysbio/syaa012. PMID 32073641.
- ↑ Swofford, David L.; Olsen, Gary J.; Waddell, Peter J.; Hillis, David M. (1996). "Phylogenetic inference". Molecular Systematics, 2nd edition. Sunderland, MA: Sinauer. pp. 407–514. ISBN 9780878932825.
- ↑ 21.0 21.1 "Overcredibility of molecular phylogenies obtained by Bayesian phylogenetics". Proceedings of the National Academy of Sciences of the United States of America 99 (25): 16138–43. December 2002. doi:10.1073/pnas.212646199. PMID 12451182. Bibcode: 2002PNAS...9916138S.
- ↑ "Bayes or bootstrap? A simulation study comparing the performance of Bayesian Markov chain Monte Carlo sampling and bootstrapping in assessing phylogenetic confidence". Molecular Biology and Evolution 20 (2): 255–66. February 2003. doi:10.1093/molbev/msg028. PMID 12598693.
- ↑ "Comparison of Bayesian and maximum likelihood bootstrap measures of phylogenetic reliability". Molecular Biology and Evolution 20 (2): 248–54. February 2003. doi:10.1093/molbev/msg042. PMID 12598692.
- ↑ "Why some clades have low bootstrap frequencies and high Bayesian posterior probabilities". Israel Journal of Ecology & Evolution 60 (1): 41–4. January 2014. doi:10.1080/15659801.2014.937900.
- ↑ Yang, Z. (18 April 2007). "Fair-Balance Paradox, Star-tree Paradox, and Bayesian Phylogenetics". Molecular Biology and Evolution 24 (8): 1639–1655. doi:10.1093/molbev/msm081. PMID 17488737.
- ↑ Yang, Ziheng; Zhu, Tianqi (20 February 2018). "Bayesian selection of misspecified models is overconfident and may cause spurious posterior probabilities for phylogenetic trees". Proceedings of the National Academy of Sciences 115 (8): 1854–1859. doi:10.1073/pnas.1712673115. PMID 29432193. Bibcode: 2018PNAS..115.1854Y.
- ↑ "Reliability of Bayesian posterior probabilities and bootstrap frequencies in phylogenetics". Systematic Biology 52 (5): 665–73. October 2003. doi:10.1080/10635150390235485. PMID 14530133.
- ↑ "MRBAYES: Bayesian inference of phylogenetic trees". Bioinformatics (Oxford, England) 17 (8): 754–5. August 2001. doi:10.1093/bioinformatics/17.8.754. PMID 11524383.
- ↑ "NEXUS: an extensible file format for systematic information". Systematic Biology 46 (4): 590–621. December 1997. doi:10.1093/sysbio/46.4.590. PMID 11975335.
- ↑ Evolution of Protein Molecules.. New York: Academic Press. 1969. pp. 21–132.
- ↑ "Maximum-likelihood estimation of phylogeny from DNA sequences when substitution rates differ over sites". Molecular Biology and Evolution 10 (6): 1396–401. November 1993. doi:10.1093/oxfordjournals.molbev.a040082. PMID 8277861.
- ↑ "MrBayes 3: Bayesian phylogenetic inference under mixed models". Bioinformatics (Oxford, England) 19 (12): 1572–4. August 2003. doi:10.1093/bioinformatics/btg180. PMID 12912839.
- ↑ "MrBayes 3.2: efficient Bayesian phylogenetic inference and model choice across a large model space". Systematic Biology 61 (3): 539–42. May 2012. doi:10.1093/sysbio/sys029. PMID 22357727.
- ↑ "Bayesian phylogenetics with BEAUti and the BEAST 1.7". Molecular Biology and Evolution 29 (8): 1969–73. August 2012. doi:10.1093/molbev/mss075. PMID 22367748.
- ↑ "BEAST 2: a software platform for Bayesian evolutionary analysis". PLOS Computational Biology 10 (4): e1003537. April 2014. doi:10.1371/journal.pcbi.1003537. PMID 24722319. Bibcode: 2014PLSCB..10E3537B.
- ↑ "A Bayesian mixture model for across-site heterogeneities in the amino-acid replacement process". Molecular Biology and Evolution 21 (6): 1095–109. June 2004. doi:10.1093/molbev/msh112. PMID 15014145.
- ↑ "BAli-Phy: simultaneous Bayesian inference of alignment and phylogeny". Bioinformatics 22 (16): 2047–8. August 2006. doi:10.1093/bioinformatics/btl175. PMID 16679334.
- ↑ "Bayesian estimation of concordance among gene trees". Molecular Biology and Evolution 24 (2): 412–26. February 2007. doi:10.1093/molbev/msl170. PMID 17095535.
- ↑ "Bayesian analysis of correlated evolution of discrete characters by reversible-jump Markov chain Monte Carlo". The American Naturalist 167 (6): 808–25. June 2006. doi:10.1086/503444. PMID 16685633.
- ↑ "Armadillo 1.1: an original workflow platform for designing and conducting phylogenetic analysis and simulations". PLOS ONE 7 (1): e29903. 2012. doi:10.1371/journal.pone.0029903. PMID 22253821. Bibcode: 2012PLoSO...729903L.
- ↑ "TOPALi v2: a rich graphical interface for evolutionary analyses of multiple alignments on HPC clusters and multi-core desktops". Bioinformatics 25 (1): 126–7. January 2009. doi:10.1093/bioinformatics/btn575. PMID 18984599.
- ↑ "Molecular phylogeny of an endemic radiation of Cuban toads (Bufonidae: Peltophryne) based on mitochondrial and nuclear genes". Journal of Biogeography 39 (3): 434–51. March 2012. doi:10.1111/j.1365-2699.2011.02594.x. Bibcode: 2012JBiog..39..434A.
- ↑ "Mass extinction, gradual cooling, or rapid radiation? Reconstructing the spatiotemporal evolution of the ancient angiosperm genus Hedyosmum (Chloranthaceae) using empirical and simulated approaches". Systematic Biology 60 (5): 596–615. October 2011. doi:10.1093/sysbio/syr062. PMID 21856636.
- ↑ "Bayesian models for comparative analysis integrating phylogenetic uncertainty". BMC Evolutionary Biology 12 (1): 102. June 2012. doi:10.1186/1471-2148-12-102. PMID 22741602. Bibcode: 2012BMCEE..12..102V.
- ↑ "Bayesian inference of character evolution". Trends in Ecology & Evolution 19 (9): 475–81. September 2004. doi:10.1016/j.tree.2004.07.002. PMID 16701310.
- ↑ "Ancestral state reconstruction reveals multiple independent evolution of diagnostic morphological characters in the "Higher Oribatida" (Acari), conflicting with current classification schemes". BMC Evolutionary Biology 10 (1): 246. August 2010. doi:10.1186/1471-2148-10-246. PMID 20701742. Bibcode: 2010BMCEE..10..246S.
- ↑ "Brunfelsia (Solanaceae): a genus evenly divided between South America and radiations on Cuba and other Antillean islands". Molecular Phylogenetics and Evolution 64 (1): 1–11. July 2012. doi:10.1016/j.ympev.2012.02.026. PMID 22425729.
- ↑ "Miocene dispersal drives island radiations in the palm tribe Trachycarpeae (Arecaceae)". Systematic Biology 61 (3): 426–42. May 2012. doi:10.1093/sysbio/syr123. PMID 22223444.
- ↑ "A phylogenetic framework for evolutionary study of the nightshades (Solanaceae): a dated 1000-tip tree". BMC Evolutionary Biology 13 (1): 214. September 2013. doi:10.1186/1471-2148-13-214. PMID 24283922. Bibcode: 2013BMCEE..13..214S.
- ↑ "Bayesian estimation of speciation and extinction from incomplete fossil occurrence data". Systematic Biology 63 (3): 349–67. May 2014. doi:10.1093/sysbio/syu006. PMID 24510972.
- ↑ "Bayesian phylogeography finds its roots". PLOS Computational Biology 5 (9): e1000520. September 2009. doi:10.1371/journal.pcbi.1000520. PMID 19779555. Bibcode: 2009PLSCB...5E0520L.
- ↑ "Assessing phenotypic correlation through the multivariate phylogenetic latent liability model". The Annals of Applied Statistics 9 (2): 969–991. 2015. doi:10.1214/15-AOAS821. ISSN 1932-6157. PMID 27053974.
- ↑ "Phylogenetic Factor Analysis" (in en). Systematic Biology 67 (3): 384–399. 2018. doi:10.1093/sysbio/syx066. ISSN 1063-5157. PMID 28950376. PMC 5920329. https://academic.oup.com/sysbio/article/67/3/384/4076231.
External links
 |
