Biography:Alexey Okulov

From HandWiki
Alexey Okulov
Born (1956-07-12) 12 July 1956 (age 68)
Russian SFSR, Soviet Union
NationalityRussia n
Alma materMoscow Institute of Physics and Technology
Known forPhase conjugation, Michelson interferometer, Bose–Einstein condensate, Angular momentum of light, Chaos theory, Soliton
Awards
Scientific career
FieldsLaser Physics, Theoretical Physics
InstitutionsLebedev Physical Institute,

A.M.Prokhorov General Physics Institute,

Moscow Institute of Physics and Technology
ThesisPeriodicity and Chaos in Structured Light

Alexey Okulov (Russian: Алексей Юрьевич Окулов) is a Soviet and Russia n physicist, the author of pioneering works in laser physics and theoretical physics.

Biography

Joined Lebedev Physical Institute Moscow in October 1979. Graduated from Moscow Institute of Physics and Technology in 1980, PhD from Lebedev Physical Institute, thesis "Periodicity and Chaos in Structured Light" in 1994.

Research

A.Yu. Okulov made substantial contributions in the optical phase conjugation, angular momentum of light, ultracold atoms theory and chaos theory. In 1979-1980 he made the seminal experiments on coherent summation of laser beams via Optical phase conjugation in stimulated Brillouin scattering.[1] The Michelson interferometer had been used to demonstrate the universal method for robust coherent summation of [math]\displaystyle{ N }[/math] laser beams with complex amplitude and phase profile. The nontrivial feature of the Michelson interferometer with stimulated Brillouin scattering mirror is that the interference pattern is insensitive to wavelength-scale phase distortions. This gives the unique opportunity to use a binary tree of [math]\displaystyle{ N-1 }[/math] beamsplitters for coherent addition of [math]\displaystyle{ N=2^n }[/math] laser amplifiers.[2] Constructive interference in an array containing [math]\displaystyle{ N-1 }[/math] beamsplitters of [math]\displaystyle{ N }[/math] laser beams synchronized by phase conjugation may increase the brightness of output amplified beam as [math]\displaystyle{ N^2 }[/math].

This work demonstrated that linewidth of the stimulated Brillouin scattering phase conjugate mirror is due to stepwise phase fluctuations[3] rather than phase diffusion responsible for conventional Schawlow-Townes Laser linewidth.[4]

In 2014 Dr. Okulov had shown that such binary-tree Michelson phase-conjugator with degenerate four-wave mixing Kerr nonlinear mirror could be used for coherent summationCite error: Closing </ref> missing for <ref> tag He had shown that due to conservation of angular momentum, the optical phase conjugation mirror experiences the optical torque in addition to Radiation pressure.[5] For these symmetry reasons, the acoustical vortices are excited inside a stimulated Brillouin scattering phase-conjugating mirror.[6] He suggested a robust Sagnac-like interferometer for the perfect optical phase conjugation of vortex photons.[7]

A.Yu.Okulov built an exact theory for the quantum condensed matter trapped by optical vortices in Gross–Pitaevskii equation mean field approach.[8] He found exact solutions describing superfluid motion in twisted optical potential mounted in slowly rotating reference frame[9]

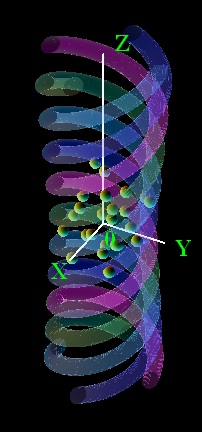
Degenerate quantum gas in vortex dipole trap with topological charge [math]\displaystyle{ \ell=2 }[/math][9].

In a field of nonlinear dynamics of lasers Alexey Okulov introduced robust and computationally efficient method of infinite dimensional maps. The nonlinear spatiotemporal effects in laser pulse propagation as spatial solitons, Talbot effect[10] and vortex lattices are computed via fast Fourier transform (FFT) and iterates of nonlinear integral mappings known from Chaos theory.[11]

  • Member of the Optical Society since 1995
  • Member of the APS since 1995
  • Member of the SPIE since 1997
  • Member of the DPG since 2021

See also

References

  1. ↑ Basov, N G; Zubarev, I G; Mironov, A B; Michailov, S I; Okulov, A Yu (1980). "Laser interferometer with wavefront reversing mirrors". Sov. Phys. JETP 52 (5): 847. Bibcode: 1980ZhETF..79.1678B. 
  2. ↑ Bowers, M W; Boyd, R W; Hankla, A K (1997). "Brillouin-enhanced four-wave-mixing vector phase-conjugate mirror with beam-combining capability". Optics Letters 22 (6): 360–362. doi:10.1364/OL.22.000360. PMID 18183201. Bibcode: 1997OptL...22..360B. 
  3. ↑ Basov, N G; Zubarev, I G; Mironov, A B; Michailov, S I; Okulov, A Yu (1980). "Phase fluctuations of the Stockes wave produced as a result of stimulated scattering of light". Sov. Phys. JETP Lett. 31 (11): 645. Bibcode: 1980JETPL..31..645B. 
  4. ↑ Schawlow, A. L.; Townes, C. H. (1958). "Infrared and optical masers". Physical Review 112 (6): 1940–1949. doi:10.1103/PhysRev.112.1940. Bibcode: 1958PhRv..112.1940S. 
  5. ↑ Lebedew, Peter (1901). "Untersuchungen über die Druckkräfte des Lichtes". Annalen der Physik 311 (11): 433–458. doi:10.1002/andp.19013111102. Bibcode: 1901AnP...311..433L. https://zenodo.org/record/1424005. 
  6. ↑ Okulov, A.Y. (2008). "Optical and Sound Helical structures in a stimulated Mandelstam – Brillouin mirror" (in ru). JETP Letters 88 (8): 561–566. doi:10.1134/s0021364008200046. Bibcode: 2008JETPL..88..487O. http://www.jetpletters.ac.ru/ps/1852/article_28262.shtml. Retrieved 2015-10-31. 
  7. ↑ Okulov, A Yu (2010). "Phase-conjugation of the isolated optical vortex using a flat surfaces". JOSA B 27 (11): 2424–2427. doi:10.1364/JOSAB.27.002424. Bibcode: 2010JOSAB..27.2424O. 
  8. ↑ A. Yu. Okulov (2012). "Cold matter trapping via slowly rotating helical potential". Phys. Lett. A 376 (4): 650–655. doi:10.1016/j.physleta.2011.11.033. Bibcode: 2012PhLA..376..650O. 
  9. ↑ 9.0 9.1 A. Yu. Okulov (2013). "Superfluid rotation sensor with helical laser trap". J. Low Temp. Phys. 171 (3): 397–407. doi:10.1007/s10909-012-0837-7. Bibcode: 2013JLTP..171..397O. 
  10. ↑ Okulov, A Yu (1990). "Two-dimensional periodic structures in nonlinear resonator". JOSA B 7 (6): 1045–1050. doi:10.1364/JOSAB.7.001045. Bibcode: 1990JOSAB...7.1045O. 
  11. ↑ Okulov, A Yu (2020). "Structured light entities, chaos and nonlocal maps". Chaos, Solitons & Fractals 133 (4): 109638. doi:10.1016/j.chaos.2020.109638. Bibcode: 2020CSF...13309638O. 




Retrieved from "https://handwiki.org/wiki/index.php?title=Biography:Alexey_Okulov&oldid=3440551"