Blichfeldt's theorem
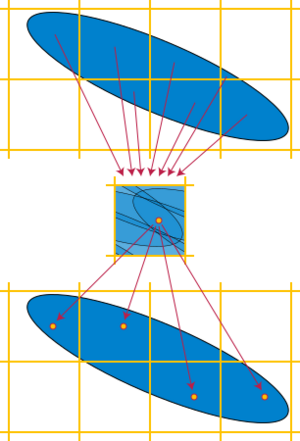
Blichfeldt's theorem is a mathematical theorem in the geometry of numbers, stating that whenever a bounded set in the Euclidean plane has area , it can be translated so that it includes at least points of the integer lattice.[1] Equivalently, every bounded set of area contains a set of points whose coordinates all differ by integers.[2]
This theorem can be generalized to other lattices and to higher dimensions, and can be interpreted as a continuous version of the pigeonhole principle.[2] It is named after Danish-American mathematician Hans Frederick Blichfeldt, who published it in 1914.[3] Some sources call it Blichfeldt's principle[4] or Blichfeldt's lemma.[5]
Statement and proof
The theorem can be stated most simply for points in the Euclidean plane, and for the integer lattice in the plane. For this version of the theorem, let be any measurable set, let denote its area, and round this number up to the next integer value, . Then Blichfeldt's theorem states that can be translated so that its translated copy contains at least points with integer coordinates.[1]
The basic idea of the proof is to cut into pieces according to the squares of the integer lattice, and to translate each of those pieces by an integer amount so that it lies within the unit square having the origin as its lower right corner. This translation may cause some pieces of the unit square to be covered more than once, but if the combined area of the translated pieces is counted with multiplicity it remains unchanged, equal to . On the other hand, if the whole unit square were covered with multiplicity its area would be , less than . Therefore, some point of the unit square must be covered with multiplicity at least . A translation that takes to the origin will also take all of the points of that covered to integer points, which is what was required.[1]
More generally, the theorem applies to -dimensional sets , with -dimensional volume , and to an arbitrary -dimensional lattice (a set of points in -dimensional space that do not all lie in any lower dimensional subspace, are separated from each other by some minimum distance, and can be combined by adding or subtracting their coordinates to produce other points in the same set). Just as the integer lattice divides the plane into squares, an arbitrary lattice divides its space into fundamental regions (called parallelotopes) with the property that any one of these regions can be translated onto any other of them by adding the coordinates of a unique lattice point. If is the -dimensional volume of one of parallelotopes, then Blichfeldt's theorem states that can be translated to include at least points of . The proof is as before: cut up by parallelotopes, translate the pieces by translation vectors in onto a single parallelotope without changing the total volume (counted with multiplicity), observe that there must be a point of multiplicity at least , and use a translation that takes to the origin.[1]
Instead of asking for a translation for which there are lattice points, an equivalent form of the theorem states that itself contains a set of points, all of whose pairwise differences belong to the lattice.[2] A strengthened version of the theorem applies to compact sets, and states that they can be translated to contain at least points of the lattice. This number of points differs from only when is an integer, for which it is larger by one.[1]
Applications
Minkowski's theorem
Minkowski's theorem, proved earlier than Blichfeldt's work by Hermann Minkowski, states that any convex set in the plane that is centrally symmetric around the origin, with area greater than four (or a compact symmetric set with area equal to four) contains a nonzero integer point. More generally, for a -dimensional lattice whose fundamental parallelotopes have volume , any set centrally symmetric around the origin with volume greater than contains a nonzero lattice point.[1]
Although Minkowski's original proof was different, Blichfeldt's theorem can be used in a simple proof of Minkowski's theorem. Let be any centrally symmetric set with volume greater than (meeting the conditions of Minkowski's theorem), and scale it down by a factor of two to obtain a set of volume greater than . By Blichfeldt's theorem, has two points and whose coordinatewise difference belongs to . Reversing the shrinking operation, and belong to . By symmetry also belongs to , and by convexity the midpoint of and belongs to . But this midpoint is , a nonzero point of .[2]
Other applications

Many applications of Blichfeldt's theorem, like the application to Minkowski's theorem, involve finding a nonzero lattice point in a large-enough set, but one that is not convex. For the proof of Minkowski's theorem, the key relation between the sets and that makes the proof work is that all differences of pairs of points in belong to . However, for a set that is not convex, might have pairs of points whose difference does not belong to , making it unusable in this technique. One could instead find the largest centrally symmetric convex subset , and then apply Minkowski's theorem to , or equivalently apply Blichfeldt's theorem to . However, in many cases a given non-convex set has a subset that is larger than , whose pairwise differences belong to . When this is the case, the larger size of relative to leads to tighter bounds on how big needs to be sure of containing a lattice point.[6]
For a centrally symmetric star domain, it is possible to use the calculus of variations to find the largest set whose pairwise differences belong to . Applications of this method include simultaneous Diophantine approximation, the problem of approximating a given set of irrational numbers by rational numbers that all have the same denominators.[6]
Generalizations
Analogues of Blichfeldt's theorem have been proven for other sets of points than lattices, showing that large enough regions contain many points from these sets. These include a theorem for Fuchsian groups, lattice-like subsets of matrices,[7] and for the sets of vertices of Archimedean tilings.[8][9]
Other generalizations allow the set to be a measurable function, proving that its sum over some set of translated lattice points is at least as large as its integral, or replace the single set with a family of sets.[10]
Computational complexity
A computational problem related to Blichfeldt's theorem has been shown to be complete for the PPP complexity class, and therefore unlikely to be solvable in polynomial time. The problem takes as input a set of integer vectors forming the basis of a -dimensional lattice , and a set of integer vectors, represented implicitly by a Boolean circuit for testing whether a given vector belongs to . It is required that the cardinality of , divided by the volume of the fundamental parallelotope of , is at least one, from which a discrete version of Blichfeldt's theorem implies that includes a pair of points whose difference belongs to . The task is to find either such a pair, or a point of that itself belongs to . The computational hardness of this task motivates the construction of a candidate for a collision-resistant cryptographic hash function.[11]
See also
- Dot planimeter, a device for estimating the area of a shape by counting the lattice points that it contains
- Pick's theorem, a more precise relationship between area and lattice points covered by a polygon with lattice-point vertices
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 "Chapter 9: A new principle in the geometry of numbers", The Geometry of Numbers, Anneli Lax New Mathematical Library, 41, Mathematical Association of America, Washington, DC, 2000, pp. 119–127, ISBN 0-88385-643-3
- ↑ 2.0 2.1 2.2 2.3 "Theorem 2.1 (Blichfeldt)", Rational quadratic forms, London Mathematical Society Monographs, 13, Academic Press, 1978, p. 68, ISBN 0-12-163260-1, https://books.google.com/books?id=6n31DAAAQBAJ&pg=PA68
- ↑ "A new principle in the geometry of numbers, with some applications", Transactions of the American Mathematical Society 15 (3): 227–235, 1914, doi:10.1090/S0002-9947-1914-1500976-6
- ↑ Marvin, Stephen (November 2012), "B", Dictionary of Scientific Principles, John Wiley & Sons, pp. 19–36, doi:10.1002/9781118582121.ch2
- ↑ "The orchard problem", Mathematical Gems I, Dolciani Mathematical Expositions, 1, Mathematical Association of America, 1973, pp. 43–53; see in particular Blichfeldt's lemma, p. 44
- ↑ 6.0 6.1 Spohn, W. G. (1968), "Blichfeldt's theorem and simultaneous Diophantine approximation", American Journal of Mathematics 90: 885–894, doi:10.2307/2373489
- ↑ Tsuji, Masatsugu (1956), "Analogue of Blichfeldt's theorem for Fuchsian groups", Commentarii Mathematici Universitatis Sancti Pauli 5: 17–24
- ↑ Cao, Penghao; Yuan, Liping (2011), "A Blichfeldt-type theorem for -points", American Mathematical Monthly 118 (8): 743–746, doi:10.4169/amer.math.monthly.118.08.743
- ↑ Schymura, Matthias; Yuan, Liping (2019), "A note on discrete lattice-periodic sets with an application to Archimedean tilings", Beiträge zur Algebra und Geometrie 60 (4): 749–759, doi:10.1007/s13366-019-00446-x
- ↑ "Section 2.6: Generalizations of the theorem of Blichfeldt", Geometry of Numbers, Bibliotheca Mathematica, 8, North-Holland, 1969, pp. 40–43
- ↑ Sotiraki, Katerina; Zampetakis, Manolis; Zirdelis, Giorgos (2018), "PPP-completeness with connections to cryptography", 59th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2018, Paris, France, October 7-9, 2018, IEEE Computer Society, pp. 148–158, doi:10.1109/FOCS.2018.00023
External links
 |

