Buchstab function

Graph of the Buchstab function ω(u) from u = 1 to u = 4.

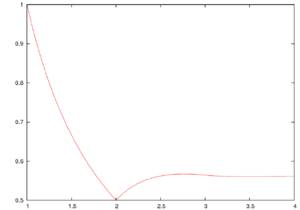
The Buchstab function (or Buchstab's function) is the unique continuous function $\omega :{\mathbb{ℝ}}_{\ge 1}\to {\mathbb{ℝ}}_{>0}$ defined by the delay differential equation

$\omega (u)=\frac{1}{u},1\le u\le 2,$

$\frac{d}{du}(u\omega (u))=\omega (u-1),u\ge 2.$

In the second equation, the derivative at u = 2 should be taken as u approaches 2 from the right. It is named after Alexander Buchstab, who wrote about it in 1937.

Asymptotics

The Buchstab function approaches $e^{-\gamma }\approx 0.561$ rapidly as $u\to \mathrm{\infty },$ where $\gamma$ is the Euler–Mascheroni constant. In fact,

$|\omega (u)-e^{-\gamma }|\le \frac{\rho (u-1)}{u},u\ge 1,$

where ρ is the Dickman function. Also, $\omega (u)-e^{-\gamma }$ oscillates in a regular way, alternating between extrema and zeroes; the extrema alternate between positive maxima and negative minima. The interval between consecutive extrema approaches 1 as u approaches infinity, as does the interval between consecutive zeroes.

Applications

The Buchstab function is used to count rough numbers. If Φ(x, y) is the number of positive integers less than or equal to x with no prime factor less than y, then for any fixed u > 1,

$\mathrm{\Phi }(x,x^{1/u})\sim \omega (u)\frac{x}{\log x^{1/u}},x\to \mathrm{\infty }.$

References

• Бухштаб, А. А. (1937), "Асимптотическая оценка одной общей теоретикочисловой функции" (in Russian), Matematicheskii Sbornik 2(44) (6): 1239–1246, http://mi.mathnet.ru/msb5649 
• "Buchstab Function", Wolfram MathWorld. Accessed on line Feb. 11, 2015.
• §IV.32, "On Φ(x,y) and Buchstab's function", Handbook of Number Theory I, József Sándor, Dragoslav S. Mitrinović, and Borislav Crstici, Springer, 2006, ISBN 978-1-4020-4215-7.
• "A differential delay equation arising from the sieve of Eratosthenes", A. Y. Cheer and D. A. Goldston, Mathematics of Computation 55 (1990), pp. 129–141.
• "An improvement of Selberg’s sieve method", W. B. Jurkat and H.-E. Richert, Acta Arithmetica 11 (1965), pp. 217–240.
• Hazewinkel, Michiel, ed. (2001), "Bukhstab function", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Bukhstab_function