Dickman function

Short description: Mathematical function

The Dickman–de Bruijn function ρ(u) plotted on a logarithmic scale. The horizontal axis is the argument u, and the vertical axis is the value of the function. The graph nearly makes a downward line on the logarithmic scale, demonstrating that the logarithm of the function is quasilinear.

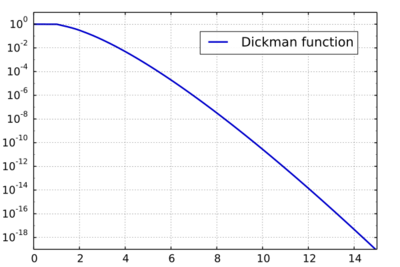
In analytic number theory, the Dickman function or Dickman–de Bruijn function ρ is a special function used to estimate the proportion of smooth numbers up to a given bound. It was first studied by actuary Karl Dickman, who defined it in his only mathematical publication. It was later studied by the Dutch mathematician Nicolaas Govert de Bruijn.

Definition

The Dickman–de Bruijn function $\rho (u)$ is a continuous function that satisfies the delay differential equation

$u{\rho }^{\prime }(u)+\rho (u-1)=0$

with initial conditions $\rho (u)=1$ for 0 ≤ u ≤ 1.

Properties

Dickman proved that, when $a$ is fixed, we have

$\mathrm{\Psi }(x,x^{1/a})\sim x\rho (a)$

where $\mathrm{\Psi }(x,y)$ is the number of y-smooth (or y-friable) integers below x. Equivalently, the number of $B$-smooth numbers less than $N$ is about $$\mathrm{\Psi }(N,B)\approx N\rho \left(\frac{\log N}{\log B}\right).$$

Ramaswami later gave a rigorous proof that for fixed a, $\mathrm{\Psi }(x,x^{1/a})$ was asymptotic to $x\rho (a)$, with the error bound

$\mathrm{\Psi }(x,x^{1/a})=x\rho (a)+O(x/\log x)$

in big O notation.

Knuth gives a proof for a narrowed bound:

$\mathrm{\Psi }(x,x^{1/a})=x\rho (a)+(1-\gamma )\rho (a-1)(x/\log x)+O(x/{(\log x)}^2)$

where γ is Euler's constant.

Applications

The Dickman–de Bruijn used to calculate the probability that the largest and 2nd largest factor of x is less than x^a

The main purpose of the Dickman–de Bruijn function is to estimate the frequency of smooth numbers at a given size. This can be used to optimize various number-theoretical algorithms such as P–1 factoring and can be useful of its own right.

It can be shown that

$\mathrm{\Psi }(x,y)=x{u}^{O(-u)}$

which is related to the estimate $\rho (u)\approx u^{-u}$ below.

The Golomb–Dickman constant has an alternate definition in terms of the Dickman–de Bruijn function.

Estimation

A first approximation might be $\rho (u)\approx u^{-u}.$ A better estimate is

$\rho (u)\sim \frac{1}{\xi \sqrt{2\pi u}}\cdot \exp (-u\xi +\mathrm{Ei}(\xi ))$

where Ei is the exponential integral and ξ is the positive root of

$e^{\xi }-1=u\xi .$

A simple upper bound is $\rho (x)\le 1/x!.$

$u$	$\rho (u)$
1	1
2	3.0685282×10−1
3	4.8608388×10−2
4	4.9109256×10−3
5	3.5472470×10−4
6	1.9649696×10−5
7	8.7456700×10−7
8	3.2320693×10−8
9	1.0162483×10−9
10	2.7701718×10−11

Computation

For each interval [n − 1, n] with n an integer, there is an analytic function ${\rho }_n$ such that ${\rho }_n(u)=\rho (u)$. For 0 ≤ u ≤ 1, $\rho (u)=1$. For 1 ≤ u ≤ 2, $\rho (u)=1-\log u$. For 2 ≤ u ≤ 3,

$\rho (u)=1-(1-\log (u-1))\log (u)+{\mathrm{Li}}_2(1-u)+\frac{{\pi }^2}{12}.$

with Li₂ the dilogarithm. Other ${\rho }_n$ can be calculated using infinite series.

An alternate method is computing lower and upper bounds with the trapezoidal rule; a mesh of progressively finer sizes allows for arbitrary accuracy. For high precision calculations (hundreds of digits), a recursive series expansion about the midpoints of the intervals is superior. Values for u ≤ 7 can be usefully computed via numerical integration in ordinary double-precision floating-point.

Extension

Friedlander defines a two-dimensional analog $\sigma (u,v)$ of $\rho (u)$. This function is used to estimate a function $\mathrm{\Psi }(x,y,z)$ similar to de Bruijn's, but counting the number of y-smooth integers with at most one prime factor greater than z. Then

$\mathrm{\Psi }(x,x^{1/a},x^{1/b})\sim x\sigma (b,a).$

This class of numbers may be encountered in the two-stage variant of P-1 factoring. However, Kruppa's estimate of the probability of finding a factor by P-1 does not make use of this result.

See also

• Buchstab function, a function used similarly to estimate the number of rough numbers, whose convergence to $e^{-\gamma }$ is controlled by the Dickman function
• Golomb–Dickman constant
• Poisson-Dirichlet distribution

Further reading

• Broadhurst, David (2010). "Dickman polylogarithms and their constants". arXiv:1004.0519 [math-ph].
• Soundararajan, Kannan (2012). "An asymptotic expansion related to the Dickman function". Ramanujan Journal 29 (1–3): 25–30. doi:10.1007/s11139-011-9304-3. 
• Weisstein, Eric W.. "Dickman function". http://mathworld.wolfram.com/DickmanFunction.html.