Butcher group

Short description: Infinite dimensional Lie group

In mathematics, the Butcher group, named after the New Zealand mathematician John C. Butcher by (Hairer Wanner), is an infinite-dimensional Lie group first introduced in numerical analysis to study solutions of non-linear ordinary differential equations by the Runge–Kutta method. It arose from an algebraic formalism involving rooted trees that provides formal power series solutions of the differential equation modeling the flow of a vector field. It was (Cayley 1857), prompted by the work of Sylvester on change of variables in differential calculus, who first noted that the derivatives of a composition of functions can be conveniently expressed in terms of rooted trees and their combinatorics.

(Connes Kreimer) pointed out that the Butcher group is the group of characters of the Hopf algebra of rooted trees that had arisen independently in their own work on renormalization in quantum field theory and Connes' work with Moscovici on local index theorems. This Hopf algebra, often called the Connes–Kreimer algebra, is essentially equivalent to the Butcher group, since its dual can be identified with the universal enveloping algebra of the Lie algebra of the Butcher group. As they commented:

“ We regard Butcher’s work on the classification of numerical integration methods as an impressive example that concrete problem-oriented work can lead to far-reaching conceptual results. ”

Differentials and rooted trees

Rooted trees with two, three and four nodes, from Cayley's original article

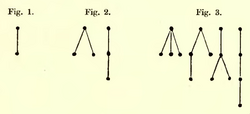
A rooted tree is a graph with a distinguished node, called the root, in which every other node is connected to the root by a unique path. If the root of a tree t is removed and the nodes connected to the original node by a single bond are taken as new roots, the tree t breaks up into rooted trees t₁, t₂, ... Reversing this process a new tree t = [t₁, t₂, ...] can be constructed by joining the roots of the trees to a new common root. The number of nodes in a tree is denoted by |t|. A heap-ordering of a rooted tree t is an allocation of the numbers 1 through |t| to the nodes so that the numbers increase on any path going away from the root. Two heap orderings are equivalent, if there is an automorphism of rooted trees mapping one of them on the other. The number of equivalence classes of heap-orderings on a particular tree is denoted by α(t) and can be computed using the Butcher's formula:

[math]\displaystyle{ \displaystyle \alpha(t)= {|t|!\over t! |S_t|}, }[/math]

where S_t denotes the symmetry group of t and the tree factorial is defined recursively by

[math]\displaystyle{ [t_1,\dots,t_n]! = |[t_1,\dots,t_n]| \cdot t_1! \cdots t_n! }[/math]

with the tree factorial of an isolated root defined to be 1

[math]\displaystyle{ \bullet ! =1. }[/math]

The ordinary differential equation for the flow of a vector field on an open subset U of R^N can be written

[math]\displaystyle{ \displaystyle {dx(s)\over ds} = f(x(s)),\,\, x(0)=x_0, }[/math]

where x(s) takes values in U, f is a smooth function from U to R^N and x₀ is the starting point of the flow at time s = 0.

(Cayley 1857) gave a method to compute the higher order derivatives x^(m)(s) in terms of rooted trees. His formula can be conveniently expressed using the elementary differentials introduced by Butcher. These are defined inductively by

[math]\displaystyle{ \delta_\bullet^i= f^i, \,\,\, \delta^i_{[t_1,\dots,t_n]} = \sum_{j_1,\dots,j_n=1}^N (\delta^{j_1}_{t_1} \cdots \delta^{j_n}_{t_n})\partial_{j_1} \cdots \partial_{j_n} f^i. }[/math]

With this notation

[math]\displaystyle{ {d^m x\over ds^m} = \sum_{|t|=m} \alpha(t) \delta_t, }[/math]

giving the power series expansion

[math]\displaystyle{ \displaystyle x(s) = x_0 + \sum_{t} {s^{|t|}\over |t|!} \alpha(t) \delta_t(0). }[/math]

As an example when N = 1, so that x and f are real-valued functions of a single real variable, the formula yields

[math]\displaystyle{ x^{(4)} = f^{\prime\prime\prime}f^3 + 3 f^{\prime\prime}f^{\prime} f^2 + f^{\prime}f^{\prime\prime} f^2 +(f^\prime)^3 f, }[/math]

where the four terms correspond to the four rooted trees from left to right in Figure 3 above.

In a single variable this formula is the same as Faà di Bruno's formula of 1855; however in several variables it has to be written more carefully in the form

[math]\displaystyle{ x^{(4)} = f^{\prime\prime\prime}(f,f,f) + 3f^{\prime\prime}(f,f^\prime(f)) + f^\prime(f^{\prime\prime}(f,f)) +f^\prime(f^\prime(f^\prime(f))), }[/math]

where the tree structure is crucial.

Definition using Hopf algebra of rooted trees

The Hopf algebra H of rooted trees was defined by (Connes Kreimer) in connection with Kreimer's previous work on renormalization in quantum field theory. It was later discovered that the Hopf algebra was the dual of a Hopf algebra defined earlier by (Grossman Larson) in a different context. The characters of H, i.e. the homomorphisms of the underlying commutative algebra into R, form a group, called the Butcher group. It corresponds to the formal group structure discovered in numerical analysis by (Butcher 1972).

The Hopf algebra of rooted trees H is defined to be the polynomial ring in the variables t, where t runs through rooted trees.

• Its comultiplication [math]\displaystyle{ \Delta:H\rightarrow H \otimes H }[/math] is defined by

[math]\displaystyle{ \Delta(t) = t\otimes I + I \otimes t +\sum_{s\subset t} s\otimes [t\backslash s], }[/math]

where the sum is over all proper rooted subtrees s of t; [math]\displaystyle{ [t\backslash s] }[/math] is the monomial given by the product the variables t_i formed by the rooted trees that arise on erasing all the nodes of s and connected links from t. The number of such trees is denoted by n(t\s).

• Its counit is the homomorphism ε of H into R sending each variable t to zero.
• Its antipode S can be defined recursively by the formula

[math]\displaystyle{ S(t) = -t - \sum_{s \subset t}(-1)^{n(t\backslash s)}S([t\backslash s])s, \,\,\, S(\bullet)= -\bullet. }[/math]

The Butcher group is defined to be the set of algebra homomorphisms φ of H into R with group structure

[math]\displaystyle{ \varphi_1 \star \varphi_2 (t)= (\varphi_1\otimes \varphi_2)\Delta(t). }[/math]

The inverse in the Butcher group is given by

[math]\displaystyle{ \varphi^{-1}(t)=\varphi(St) }[/math]

and the identity by the counit ε.

Using complex coefficients in the construction of the Hopf algebra of rooted trees one obtains the complex Hopf algebra of rooted trees. Its C-valued characters form a group, called the complex Butcher group G_C. The complex Butcher group G_C is an infinite-dimensional complex Lie group which appears as a toy model in the § Renormalization of quantum field theories.

Butcher series and Runge–Kutta method

The non-linear ordinary differential equation

[math]\displaystyle{ {dx(s)\over ds} = f(x(s)),\,\,\, x(0)=x_0, }[/math]

can be solved approximately by the Runge–Kutta method. This iterative scheme requires an m x m matrix

[math]\displaystyle{ A=(a_{ij}) }[/math]

and a vector

[math]\displaystyle{ b=(b_i) }[/math]

with m components.

The scheme defines vectors x_n by first finding a solution X₁, ... , X_m of

[math]\displaystyle{ X_i= x_{n-1} + h \sum_{j=1}^m a_{ij} f(X_j) }[/math]

and then setting

[math]\displaystyle{ x_n=x_{n-1} +h \sum_{j=1}^m b_j f(x_j). }[/math]

(Butcher 1963) showed that the solution of the corresponding ordinary differential equations

[math]\displaystyle{ X_i(s)=x_0 + s\sum_{j=1}^m a_{ij} f(X_j(s)),\,\,\, x(s)=x_0 + s \sum_{j=1}^m b_jf(X_j(s)) }[/math]

has the power series expansion

[math]\displaystyle{ X_i(s) = x_0 +\sum_t {s^{|t|}\over |t|!} \alpha(t) t! \sum_{j=1}^m a_{ij} \varphi_j(t)\delta_t(0),\,\,\,\,x(s) = x_0 + \sum_t {s^{|t|}\over |t|!} \alpha(t) t! \varphi(t)\delta_t(0), }[/math]

where φ_j and φ are determined recursively by

[math]\displaystyle{ \varphi_j(\bullet)=1.\,\,\, \varphi_i([t_1,\cdots,t_k])=\sum_{j_1,\dots,j_k} a_{ij_1}\dots a_{ij_k} \varphi_{j_1}(t_1)\dots \varphi_{j_k}(t_k) }[/math]

and

[math]\displaystyle{ \varphi(t) = \sum_{j=1}^m b_j \varphi_j(t). }[/math]

The power series above are called B-series or Butcher series. The corresponding assignment φ is an element of the Butcher group. The homomorphism corresponding to the actual flow has

[math]\displaystyle{ \Phi(t)={1\over t!}. }[/math]

Butcher showed that the Runge–Kutta method gives an nth order approximation of the actual flow provided that φ and Φ agree on all trees with n nodes or less. Moreover, (Butcher 1972) showed that the homomorphisms defined by the Runge–Kutta method form a dense subgroup of the Butcher group: in fact he showed that, given a homomorphism φ', there is a Runge–Kutta homomorphism φ agreeing with φ' to order n; and that if given homomorphims φ and φ' corresponding to Runge–Kutta data (A, b) and (A' , b' ), the product homomorphism [math]\displaystyle{ \varphi\star \varphi^\prime }[/math] corresponds to the data

[math]\displaystyle{ \begin{pmatrix} A & 0\\ 0 & A^\prime\\ \end{pmatrix},\,\, (b,b^\prime). }[/math]

(Hairer Wanner) proved that the Butcher group acts naturally on the functions f. Indeed, setting

[math]\displaystyle{ \varphi\circ f= 1 +\sum_t {s^{|t|}\over |t|!} \alpha(t) t! \varphi(t)\delta_t(0), }[/math]

they proved that

[math]\displaystyle{ \varphi_1\circ (\varphi_2\circ f) = (\varphi_1\star \varphi_2)\circ f. }[/math]

Lie algebra

(Connes Kreimer) showed that associated with the Butcher group G is an infinite-dimensional Lie algebra. The existence of this Lie algebra is predicted by a theorem of (Milnor Moore): the commutativity and natural grading on H implies that the graded dual H* can be identified with the universal enveloping algebra of a Lie algebra [math]\displaystyle{ \mathfrak{g} }[/math]. Connes and Kreimer explicitly identify [math]\displaystyle{ \mathfrak{g} }[/math] with a space of derivations θ of H into R, i.e. linear maps such that

[math]\displaystyle{ \theta(ab)=\varepsilon(a)\theta(b) + \theta(a)\varepsilon(b), }[/math]

the formal tangent space of G at the identity ε. This forms a Lie algebra with Lie bracket

[math]\displaystyle{ [\theta_1,\theta_2](t)=(\theta_1 \otimes \theta_2 -\theta_2\otimes\theta_1)\Delta(t). }[/math]

[math]\displaystyle{ \mathfrak{g} }[/math] is generated by the derivations θ_t defined by

[math]\displaystyle{ \theta_t(t^\prime)=\delta_{tt^\prime}, }[/math]

for each rooted tree t.

The infinite-dimensional Lie algebra [math]\displaystyle{ \mathfrak{g} }[/math] from (Connes Kreimer) and the Lie algebra L(G) of the Butcher group as an infinite-dimensional Lie group are not the same. The Lie algebra L(G) can be identified with the Lie algebra of all derivations in the dual of H (i.e. the space of all linear maps from H to R), whereas [math]\displaystyle{ \mathfrak{g} }[/math] is obtained from the graded dual. Hence [math]\displaystyle{ \mathfrak{g} }[/math] turns out to be a (strictly smaller) Lie subalgebra of L(G).

Renormalization

(Connes Kreimer) provided a general context for using Hopf algebraic methods to give a simple mathematical formulation of renormalization in quantum field theory. Renormalization was interpreted as Birkhoff factorization of loops in the character group of the associated Hopf algebra. The models considered by (Kreimer 1999) had Hopf algebra H and character group G, the Butcher group. (Brouder 2000) has given an account of this renormalization process in terms of Runge–Kutta data.

In this simplified setting, a renormalizable model has two pieces of input data:

• a set of Feynman rules given by an algebra homomorphism Φ of H into the algebra V of Laurent series in z with poles of finite order;
• a renormalization scheme given by a linear operator R on V such that R satisfies the Rota–Baxter identity

[math]\displaystyle{ R(fg) + R(f)R(g) = R(fR(g)) + R(R(f)g) }[/math]

and the image of R – id lies in the algebra V₊ of power series in z.

Note that R satisfies the Rota–Baxter identity if and only if id – R does. An important example is the minimal subtraction scheme

[math]\displaystyle{ \displaystyle R(\sum_{n} a_n z^n )= \sum_{n\lt 0} a_n z^n. }[/math]

In addition there is a projection P of H onto the augmentation ideal ker ε given by

[math]\displaystyle{ \displaystyle P(x) = x -\varepsilon(x)1. }[/math]

To define the renormalized Feynman rules, note that the antipode S satisfies

[math]\displaystyle{ m\circ (S\otimes {\rm id}) \Delta (x) =\varepsilon(x)1 }[/math]

so that

[math]\displaystyle{ S = - m\circ (S\otimes P)\Delta, }[/math]

The renormalized Feynman rules are given by a homomorphism [math]\displaystyle{ \Phi_S^R }[/math] of H into V obtained by twisting the homomorphism Φ • S. The homomorphism [math]\displaystyle{ \Phi_S^R }[/math] is uniquely specified by

[math]\displaystyle{ \Phi_S^R = -m(S\otimes \Phi_S^R\circ P)\Delta. }[/math]

Because of the precise form of Δ, this gives a recursive formula for [math]\displaystyle{ \Phi_S^R }[/math].

For the minimal subtraction scheme, this process can be interpreted in terms of Birkhoff factorization in the complex Butcher group. Φ can be regarded as a map γ of the unit circle into the complexification G_C of G (maps into C instead of R). As such it has a Birkhoff factorization

[math]\displaystyle{ \displaystyle \gamma(z)=\gamma_-(z)^{-1} \gamma_+(z), }[/math]

where γ₊ is holomorphic on the interior of the closed unit disk and γ_– is holomorphic on its complement in the Riemann sphere C [math]\displaystyle{ \cup\{\infty\} }[/math] with γ_–(∞) = 1. The loop γ₊ corresponds to the renormalized homomorphism. The evaluation at z = 0 of γ₊ or the renormalized homomorphism gives the dimensionally regularized values for each rooted tree.

In example, the Feynman rules depend on additional parameter μ, a "unit of mass". (Connes Kreimer) showed that

[math]\displaystyle{ \partial_\mu \gamma_{\mu-} =0, }[/math]

so that γ_μ– is independent of μ.

The complex Butcher group comes with a natural one-parameter group λ_w of automorphisms, dual to that on H

[math]\displaystyle{ \lambda_{w}(t)= w^{|t|}t }[/math]

for w ≠ 0 in C.

The loops γ_μ and λ_w · γ_μ have the same negative part and, for t real,

[math]\displaystyle{ \displaystyle F_t=\lim_{z=0} \gamma_-(z) \lambda_{tz}(\gamma_-(z)^{-1}) }[/math]

defines a one-parameter subgroup of the complex Butcher group G_C called the renormalization group flow (RG).

Its infinitesimal generator β is an element of the Lie algebra of G_C and is defined by

[math]\displaystyle{ \beta=\partial_t F_t|_{t=0}. }[/math]

It is called the beta-function of the model.

In any given model, there is usually a finite-dimensional space of complex coupling constants. The complex Butcher group acts by diffeomorphisms on this space. In particular the renormalization group defines a flow on the space of coupling constants, with the beta function giving the corresponding vector field.

More general models in quantum field theory require rooted trees to be replaced by Feynman diagrams with vertices decorated by symbols from a finite index set. Connes and Kreimer have also defined Hopf algebras in this setting and have shown how they can be used to systematize standard computations in renormalization theory.

Example

(Kreimer 2007) has given a "toy model" involving dimensional regularization for H and the algebra V. If c is a positive integer and q_μ = q / μ is a dimensionless constant, Feynman rules can be defined recursively by

[math]\displaystyle{ \displaystyle \Phi([t_1,\dots, t_n])=\int {\Phi(t_1)\cdots \Phi(t_n) \over |y|^2 + q_\mu^2} (|y|^2)^{-z({c\over 2} -1)} \, d^D y, }[/math]

where z = 1 – D/2 is the regularization parameter. These integrals can be computed explicitly in terms of the Gamma function using the formula

[math]\displaystyle{ \displaystyle \int {(|y|^2)^{-u}\over |y|^2 +q_\mu^2} \, d^Dy = \pi^{D/2} (q_\mu^2)^{-z-u} {\Gamma(-u +D/2)\Gamma(1+u-D/2)\over \Gamma(D/2)}. }[/math]

In particular

[math]\displaystyle{ \displaystyle \Phi(\bullet)=\pi^{D/2}(q_\mu^2)^{-zc/2}{\Gamma(1+cz)\over cz}. }[/math]

Taking the renormalization scheme R of minimal subtraction, the renormalized quantities [math]\displaystyle{ \Phi_S^R(t) }[/math] are polynomials in [math]\displaystyle{ \log q_\mu^2 }[/math] when evaluated at z = 0.

References

• Bergbauer, Christoph; Kreimer, Dirk (2005), "The Hopf Algebra of Rooted Trees in Epstein-Glaser Renormalization", Annales Henri Poincaré 6 (2): 343–367, doi:10.1007/s00023-005-0210-3, Bibcode: 2005AnHP....6..343B 
• Boutet de Monvel, Louis (2003), "Algèbre de Hopf des diagrammes de Feynman, renormalisation et factorisation de Wiener-Hopf (d'après A. Connes et D. Kreimer). [Hopf algebra of Feynman diagrams, renormalization and Wiener-Hopf factorization (following A. Connes and D. Kreimer)"], Astérisque, Séminaire Bourbaki 290: 149–165, http://people.math.jussieu.fr/~boutet/renormalisation.pdf 
• Brouder, Christian (2000), "Runge–Kutta methods and renormalization", Eur. Phys. J. C 12 (3): 521–534, doi:10.1007/s100529900235, Bibcode: 2000EPJC...12..521B 
• Bogfjellmo, G.; Schmeding, A. (2015), "The Lie group structure of the Butcher group", Foundations of Computational Mathematics 17 (1): 127–159, doi:10.1007/s10208-015-9285-5 
• Brouder, Christian (2004), "Trees, Renormalization and Differential Equations", BIT Numerical Mathematics 44 (3): 425–438, doi:10.1023/B:BITN.0000046809.66837.cc 
• Butcher, J.C (1963), "Coefficients for the study of Runge-Kutta integration processes", J. Austral. Math. Soc. 3 (2): 185–201, doi:10.1017/S1446788700027932 
• Butcher, J.C (1972), "An algebraic theory of integration methods", Math. Comput. 26 (117): 79–106, doi:10.2307/2004720 
• Butcher, John C. (2008), Numerical methods for ordinary differential equations (2nd ed.), John Wiley & Sons Ltd., ISBN 978-0-470-72335-7 
• Butcher, J.C (2009), "Trees and numerical methods for ordinary differential equations", Numerical Algorithms 53 (2–3): 153–170, doi:10.1007/s11075-009-9285-0 
• Cayley, Arthur (1857), "On the theory of analytic forms called trees", Philosophical Magazine XIII: 172–176, https://archive.org/stream/collectedmathema03cayluoft#page/242/mode/1up  (also in Volume 3 of the Collected Works of Cayley, pages 242–246)
• Connes, Alain; Kreimer, Dirk (1998), "Hopf Algebras, Renormalization and Noncommutative Geometry", Communications in Mathematical Physics 199 (1): 203–242, doi:10.1007/s002200050499, Bibcode: 1998CMaPh.199..203C, http://www.alainconnes.org/docs/ncgk.pdf 
• Connes, Alain; Kreimer, Dirk (1999), "Lessons from quantum field theory: Hopf algebras and spacetime geometries", Letters in Mathematical Physics 48: 85–96, doi:10.1023/A:1007523409317 
• Connes, Alain; Kreimer, Dirk (2000), "Renormalization in quantum field theory and the Riemann-Hilbert problem. I. The Hopf algebra structure of graphs and the main theorem", Commun. Math. Phys. 210 (1): 249–273, doi:10.1007/s002200050779, Bibcode: 2000CMaPh.210..249C, http://www.alainconnes.org/docs/RH1.pdf 
• Connes, Alain; Kreimer, Dirk (2001), "Renormalization in quantum field theory and the Riemann-Hilbert problem. II. The β-function, diffeomorphisms and the renormalization group", Commun. Math. Phys. 216 (1): 215–241, doi:10.1007/PL00005547, Bibcode: 2001CMaPh.216..215C, http://www.alainconnes.org/docs/RH2.pdf 
• Gracia-Bondía, José; Várilly, Joseph C.; Figueroa, Héctor (2000), Elements of noncommutative geometry, Birkhäuser, ISBN 978-0-8176-4124-5 , Chapter 14.
• Grossman, R.; Larson, R. (1989), "Hopf algebraic structures of families of trees", Journal of Algebra 26: 184–210, doi:10.1016/0021-8693(89)90328-1 
• Hairer, E.; Wanner, G. (1974), "On the Butcher group and general multi-value methods", Computing 13: 1–15, doi:10.1007/BF02268387 
• Kreimer, Dirk (1998), "On the Hopf algebra structure of perturbative quantum field theories", Adv. Theor. Math. Phys. 2 (2): 303–334, doi:10.4310/ATMP.1998.v2.n2.a4, Bibcode: 1997q.alg.....7029K 
• Kreimer, Dirk (1999), "Chen's iterated integral represents the operator product expansion", Adv. Theor. Math. Phys. 3 (3): 627–670, doi:10.4310/ATMP.1999.v3.n3.a7, Bibcode: 1999hep.th....1099K 
• Kreimer, Dirk (2007), Factorization in Quantum Field Theory: An Exercise in Hopf Algebras and Local Singularities, Frontiers in Number Theory, Physics, and Geometry II, Springer, pp. 715–736, Bibcode: 2003hep.th....6020K 
• Milnor, John Willard; Moore, John C. (1965), "On the structure of Hopf algebras", Annals of Mathematics, Second Series 81 (2): 211–264, doi:10.2307/1970615, https://polipapers.upv.es/index.php/AGT/article/view/2250 
• John C. Butcher: "B-Series : Algebraic Analysis of Numerical Methods", Springer（SSCM, volume 55), ISBN 978-3030709556 (April, 2021).