Physics:Renormalization
| Renormalization and regularization |
|---|
| Quantum field theory |
|---|
 |
| History |
Renormalization is a collection of techniques in quantum field theory, statistical field theory, and the theory of self-similar geometric structures, that are used to treat infinities arising in calculated quantities by altering values of these quantities to compensate for effects of their self-interactions. But even if no infinities arose in loop diagrams in quantum field theory, it could be shown that it would be necessary to renormalize the mass and fields appearing in the original Lagrangian.[1]
For example, an electron theory may begin by postulating an electron with an initial mass and charge. In quantum field theory a cloud of virtual particles, such as photons, positrons, and others surrounds and interacts with the initial electron. Accounting for the interactions of the surrounding particles (e.g. collisions at different energies) shows that the electron-system behaves as if it had a different mass and charge than initially postulated. Renormalization, in this example, mathematically replaces the initially postulated mass and charge of an electron with the experimentally observed mass and charge. Mathematics and experiments prove that positrons and more massive particles like protons exhibit precisely the same observed charge as the electron – even in the presence of much stronger interactions and more intense clouds of virtual particles.
Renormalization specifies relationships between parameters in the theory when parameters describing large distance scales differ from parameters describing small distance scales. Physically, the pileup of contributions from an infinity of scales involved in a problem may then result in further infinities. When describing spacetime as a continuum, certain statistical and quantum mechanical constructions are not well-defined. To define them, or make them unambiguous, a continuum limit must carefully remove "construction scaffolding" of lattices at various scales. Renormalization procedures are based on the requirement that certain physical quantities (such as the mass and charge of an electron) equal observed (experimental) values. That is, the experimental value of the physical quantity yields practical applications, but due to their empirical nature the observed measurement represents areas of quantum field theory that require deeper derivation from theoretical bases.
Renormalization was first developed in quantum electrodynamics (QED) to make sense of infinite integrals in perturbation theory. Initially viewed as a suspect provisional procedure even by some of its originators, renormalization eventually was embraced as an important and self-consistent actual mechanism of scale physics in several fields of physics and mathematics. Despite his later skepticism, it was Paul Dirac who pioneered renormalization.[2][3]
Today, the point of view has shifted: on the basis of the breakthrough renormalization group insights of Nikolay Bogolyubov and Kenneth Wilson, the focus is on variation of physical quantities across contiguous scales, while distant scales are related to each other through "effective" descriptions. All scales are linked in a broadly systematic way, and the actual physics pertinent to each is extracted with the suitable specific computational techniques appropriate for each. Wilson clarified which variables of a system are crucial and which are redundant.
Renormalization is distinct from regularization, another technique to control infinities by assuming the existence of new unknown physics at new scales.
Self-interactions in classical physics

The problem of infinities first arose in the classical electrodynamics of point particles in the 19th and early 20th century.
The mass of a charged particle should include the mass–energy in its electrostatic field (electromagnetic mass). Assume that the particle is a charged spherical shell of radius re. The mass–energy in the field is
which becomes infinite as re → 0. This implies that the point particle would have infinite inertia and thus cannot be accelerated. Incidentally, the value of re that makes equal to the electron mass is called the classical electron radius, which (setting and restoring factors of c and ) turns out to be
where is the fine-structure constant, and is the reduced Compton wavelength of the electron.
Renormalization: The total effective mass of a spherical charged particle includes the actual bare mass of the spherical shell (in addition to the mass mentioned above associated with its electric field). If the shell's bare mass is allowed to be negative, it might be possible to take a consistent point limit.[citation needed] This was called renormalization, and Lorentz and Abraham attempted to develop a classical theory of the electron this way. This early work was the inspiration for later attempts at regularization and renormalization in quantum field theory.
(See also regularization (physics) for an alternative way to remove infinities from this classical problem, assuming new physics exists at small scales.)
When calculating the electromagnetic interactions of charged particles, it is tempting to ignore the back-reaction of a particle's own field on itself. (Analogous to the back-EMF of circuit analysis.) But this back-reaction is necessary to explain the friction on charged particles when they emit radiation. If the electron is assumed to be a point, the value of the back-reaction diverges, for the same reason that the mass diverges, because the field is inverse-square.
The Abraham–Lorentz theory had a noncausal "pre-acceleration". Sometimes an electron would start moving before the force is applied. This is a sign that the point limit is inconsistent.
The trouble was worse in classical field theory than in quantum field theory, because in quantum field theory a charged particle experiences Zitterbewegung due to interference with virtual particle–antiparticle pairs, thus effectively smearing out the charge over a region comparable to the Compton wavelength. In quantum electrodynamics at small coupling, the electromagnetic mass only diverges as the logarithm of the radius of the particle.
Divergences in quantum electrodynamics
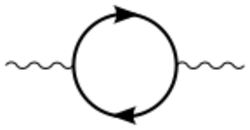


When developing quantum electrodynamics in the 1930s, Max Born, Werner Heisenberg, Pascual Jordan, and Paul Dirac discovered that in perturbative corrections many integrals were divergent (see The problem of infinities).
One way of describing the perturbation theory corrections' divergences was discovered in 1947–49 by Hans Kramers,[4] Hans Bethe,[5] Julian Schwinger,[6][7][8][9] Richard Feynman,[10][11][12] and Shin'ichiro Tomonaga,[13][14][15][16][17][18][19] and systematized by Freeman Dyson in 1949.[20] The divergences appear in radiative corrections involving Feynman diagrams with closed loops of virtual particles in them.
While virtual particles obey conservation of energy and momentum, they can have any energy and momentum, even one that is not allowed by the relativistic energy–momentum relation for the observed mass of that particle (that is, is not necessarily the squared mass of the particle in that process, e.g. for a photon it could be nonzero). Such a particle is called off-shell. When there is a loop, the momentum of the particles involved in the loop is not uniquely determined by the energies and momenta of incoming and outgoing particles. A variation in the energy of one particle in the loop can be balanced by an equal and opposite change in the energy of another particle in the loop, without affecting the incoming and outgoing particles. Thus many variations are possible. So to find the amplitude for the loop process, one must integrate over all possible combinations of energy and momentum that could travel around the loop.
These integrals are often divergent, that is, they give infinite answers. The divergences that are significant are the "ultraviolet" (UV) ones. An ultraviolet divergence can be described as one that comes from
- the region in the integral where all particles in the loop have large energies and momenta,
- very short wavelengths and high-frequencies fluctuations of the fields, in the path integral for the field,
- very short proper-time between particle emission and absorption, if the loop is thought of as a sum over particle paths.
So these divergences are short-distance, short-time phenomena.
Shown in the pictures at the right margin, there are exactly three one-loop divergent loop diagrams in quantum electrodynamics:[21]
- (a) A photon creates a virtual electron–positron pair, which then annihilates. This is a vacuum polarization diagram.
- (b) An electron quickly emits and reabsorbs a virtual photon, called a self-energy.
- (c) An electron emits a photon, emits a second photon, and reabsorbs the first. This process is shown in the section below in figure 2, and it is called a vertex renormalization. The Feynman diagram for this is also called a “penguin diagram” due to its shape remotely resembling a penguin.
The three divergences correspond to the three parameters in the theory under consideration:
- The field normalization Z.
- The mass of the electron.
- The charge of the electron.
The second class of divergence called an infrared divergence, is due to massless particles, like the photon. Every process involving charged particles emits infinitely many coherent photons of infinite wavelength, and the amplitude for emitting any finite number of photons is zero. For photons, these divergences are well understood. For example, at the 1-loop order, the vertex function has both ultraviolet and infrared divergences. In contrast to the ultraviolet divergence, the infrared divergence does not require the renormalization of a parameter in the theory involved. The infrared divergence of the vertex diagram is removed by including a diagram similar to the vertex diagram with the following important difference: the photon connecting the two legs of the electron is cut and replaced by two on-shell (i.e. real) photons whose wavelengths tend to infinity; this diagram is equivalent to the bremsstrahlung process. This additional diagram must be included because there is no physical way to distinguish a zero-energy photon flowing through a loop as in the vertex diagram and zero-energy photons emitted through bremsstrahlung. From a mathematical point of view, the IR divergences can be regularized by assuming fractional differentiation w.r.t. a parameter, for example:
is well defined at p = a but is UV divergent; if we take the 3⁄2-th fractional derivative with respect to −a2, we obtain the IR divergence
so we can cure IR divergences by turning them into UV divergences.[clarification needed]
A loop divergence

The diagram in Figure 2 shows one of the several one-loop contributions to electron–electron scattering in QED. The electron on the left side of the diagram, represented by the solid line, starts out with 4-momentum pμ and ends up with 4-momentum rμ. It emits a virtual photon carrying rμ − pμ to transfer energy and momentum to the other electron. But in this diagram, before that happens, it emits another virtual photon carrying 4-momentum qμ, and it reabsorbs this one after emitting the other virtual photon. Energy and momentum conservation do not determine the 4-momentum qμ uniquely, so all possibilities contribute equally and we must integrate.
This diagram's amplitude ends up with, among other things, a factor from the loop of
The various γμ factors in this expression are gamma matrices as in the covariant formulation of the Dirac equation; they have to do with the spin of the electron. The factors of e are the electric coupling constant, while the provide a heuristic definition of the contour of integration around the poles in the space of momenta. The important part for our purposes is the dependency on qμ of the three big factors in the integrand, which are from the propagators of the two electron lines and the photon line in the loop.
This has a piece with two powers of qμ on top that dominates at large values of qμ (Pokorski 1987, p. 122):
This integral is divergent and infinite, unless we cut it off at finite energy and momentum in some way.
Similar loop divergences occur in other quantum field theories.
Renormalized and bare quantities
The solution was to realize that the quantities initially appearing in the theory's formulae (such as the formula for the Lagrangian), representing such things as the electron's electric charge and mass, as well as the normalizations of the quantum fields themselves, did not actually correspond to the physical constants measured in the laboratory. As written, they were bare quantities that did not take into account the contribution of virtual-particle loop effects to the physical constants themselves. Among other things, these effects would include the quantum counterpart of the electromagnetic back-reaction that so vexed classical theorists of electromagnetism. In general, these effects would be just as divergent as the amplitudes under consideration in the first place; so finite measured quantities would, in general, imply divergent bare quantities.
To make contact with reality, then, the formulae would have to be rewritten in terms of measurable, renormalized quantities. The charge of the electron, say, would be defined in terms of a quantity measured at a specific kinematic renormalization point or subtraction point (which will generally have a characteristic energy, called the renormalization scale or simply the energy scale). The parts of the Lagrangian left over, involving the remaining portions of the bare quantities, could then be reinterpreted as counterterms, involved in divergent diagrams exactly canceling out the troublesome divergences for other diagrams.
Renormalization in QED

For example, in the Lagrangian of QED
the fields and coupling constant are really bare quantities, hence the subscript B above. Conventionally the bare quantities are written so that the corresponding Lagrangian terms are multiples of the renormalized ones:
Gauge invariance, via a Ward–Takahashi identity, turns out to imply that we can renormalize the two terms of the covariant derivative piece
together (Pokorski 1987, p. 115), which is what happened to Z2; it is the same as Z1.
A term in this Lagrangian, for example, the electron–photon interaction pictured in Figure 1, can then be written
The physical constant e, the electron's charge, can then be defined in terms of some specific experiment: we set the renormalization scale equal to the energy characteristic of this experiment, and the first term gives the interaction we see in the laboratory (up to small, finite corrections from loop diagrams, providing such exotica as the high-order corrections to the magnetic moment). The rest is the counterterm. If the theory is renormalizable (see below for more on this), as it is in QED, the divergent parts of loop diagrams can all be decomposed into pieces with three or fewer legs, with an algebraic form that can be canceled out by the second term (or by the similar counterterms that come from Z0 and Z3).
The diagram with the Z1 counterterm's interaction vertex placed as in Figure 3 cancels out the divergence from the loop in Figure 2.
Historically, the splitting of the "bare terms" into the original terms and counterterms came before the renormalization group insight due to Kenneth Wilson.[22] According to such renormalization group insights, detailed in the next section, this splitting is unnatural and actually unphysical, as all scales of the problem enter in continuous systematic ways.
Running couplings
To minimize the contribution of loop diagrams to a given calculation (and therefore make it easier to extract results), one chooses a renormalization point close to the energies and momenta exchanged in the interaction. However, the renormalization point is not itself a physical quantity: the physical predictions of the theory, calculated to all orders, should in principle be independent of the choice of renormalization point, as long as it is within the domain of application of the theory. Changes in renormalization scale will simply affect how much of a result comes from Feynman diagrams without loops, and how much comes from the remaining finite parts of loop diagrams. One can exploit this fact to calculate the effective variation of physical constants with changes in scale. This variation is encoded by beta-functions, and the general theory of this kind of scale-dependence is known as the renormalization group.
Colloquially, particle physicists often speak of certain physical "constants" as varying with the energy of interaction, though in fact, it is the renormalization scale that is the independent quantity. This running does, however, provide a convenient means of describing changes in the behavior of a field theory under changes in the energies involved in an interaction. For example, since the coupling in quantum chromodynamics becomes small at large energy scales, the theory behaves more like a free theory as the energy exchanged in an interaction becomes large – a phenomenon known as asymptotic freedom. Choosing an increasing energy scale and using the renormalization group makes this clear from simple Feynman diagrams; were this not done, the prediction would be the same, but would arise from complicated high-order cancellations.
For example,
is ill-defined.
To eliminate the divergence, simply change lower limit of integral into εa and εb:
Making sure εb/εa → 1, then I = ln a/b.
Regularization
Since the quantity ∞ − ∞ is ill-defined, in order to make this notion of canceling divergences precise, the divergences first have to be tamed mathematically using the theory of limits, in a process known as regularization (Weinberg, 1995).
An essentially arbitrary modification to the loop integrands, or regulator, can make them drop off faster at high energies and momenta, in such a manner that the integrals converge. A regulator has a characteristic energy scale known as the cutoff; taking this cutoff to infinity (or, equivalently, the corresponding length/time scale to zero) recovers the original integrals.
With the regulator in place, and a finite value for the cutoff, divergent terms in the integrals then turn into finite but cutoff-dependent terms. After canceling out these terms with the contributions from cutoff-dependent counterterms, the cutoff is taken to infinity and finite physical results recovered. If physics on scales we can measure is independent of what happens at the very shortest distance and time scales, then it should be possible to get cutoff-independent results for calculations.
Many different types of regulator are used in quantum field theory calculations, each with its advantages and disadvantages. One of the most popular in modern use is dimensional regularization, invented by Gerardus 't Hooft and Martinus J. G. Veltman,[23] which tames the integrals by carrying them into a space with a fictitious fractional number of dimensions. Another is Pauli–Villars regularization, which adds fictitious particles to the theory with very large masses, such that loop integrands involving the massive particles cancel out the existing loops at large momenta.
Yet another regularization scheme is the lattice regularization, introduced by Kenneth Wilson, which pretends that hyper-cubical lattice constructs our spacetime with fixed grid size. This size is a natural cutoff for the maximal momentum that a particle could possess when propagating on the lattice. And after doing a calculation on several lattices with different grid size, the physical result is extrapolated to grid size 0, or our natural universe. This presupposes the existence of a scaling limit.
A rigorous mathematical approach to renormalization theory is the so-called causal perturbation theory, where ultraviolet divergences are avoided from the start in calculations by performing well-defined mathematical operations only within the framework of distribution theory. In this approach, divergences are replaced by ambiguity: corresponding to a divergent diagram is a term which now has a finite, but undetermined, coefficient. Other principles, such as gauge symmetry, must then be used to reduce or eliminate the ambiguity.
Zeta function regularization
Julian Schwinger discovered a relationship[citation needed] between zeta function regularization and renormalization, using the asymptotic relation:
as the regulator Λ → ∞. Based on this, he considered using the values of ζ(−n) to get finite results. Although he reached inconsistent results, an improved formula studied by Hartle, J. Garcia, and based on the works by E. Elizalde includes the technique of the zeta regularization algorithm
where the B's are the Bernoulli numbers and
So every I(m, Λ) can be written as a linear combination of ζ(−1), ζ(−3), ζ(−5), ..., ζ(−m).
Or simply using Abel–Plana formula we have for every divergent integral:
valid when m > 0. Here the zeta function is Hurwitz zeta function and Beta is a positive real number.
The "geometric" analogy is given by, (if we use rectangle method) to evaluate the integral so:
Using Hurwitz zeta regularization plus the rectangle method with step h (not to be confused with the Planck constant).
The logarithmic divergent integral has the regularization
since for the Harmonic series in the limit we must recover the series
For multi-loop integrals that will depend on several variables we can make a change of variables to polar coordinates and then replace the integral over the angles by a sum so we have only a divergent integral, that will depend on the modulus and then we can apply the zeta regularization algorithm, the main idea for multi-loop integrals is to replace the factor after a change to hyperspherical coordinates F(r, Ω) so the UV overlapping divergences are encoded in variable r. In order to regularize these integrals one needs a regulator, for the case of multi-loop integrals, these regulator can be taken as
so the multi-loop integral will converge for big enough s using the Zeta regularization we can analytic continue the variable s to the physical limit where s = 0 and then regularize any UV integral, by replacing a divergent integral by a linear combination of divergent series, which can be regularized in terms of the negative values of the Riemann zeta function ζ(−m).
Attitudes and interpretation
The early formulators of QED and other quantum field theories were, as a rule, dissatisfied with this state of affairs. It seemed illegitimate to do something tantamount to subtracting infinities from infinities to get finite answers.
Freeman Dyson argued that these infinities are of a basic nature and cannot be eliminated by any formal mathematical procedures, such as the renormalization method.[24][25]
Dirac's criticism was the most persistent.[26] As late as 1975, he was saying:[27]
- Most physicists are very satisfied with the situation. They say: 'Quantum electrodynamics is a good theory and we do not have to worry about it any more.' I must say that I am very dissatisfied with the situation because this so-called 'good theory' does involve neglecting infinities which appear in its equations, ignoring them in an arbitrary way. This is just not sensible mathematics. Sensible mathematics involves disregarding a quantity when it is small – not neglecting it just because it is infinitely great and you do not want it!
Another important critic was Feynman. Despite his crucial role in the development of quantum electrodynamics, he wrote the following in 1985:[28]
- The shell game that we play is technically called 'renormalization'. But no matter how clever the word, it is still what I would call a dippy process! Having to resort to such hocus-pocus has prevented us from proving that the theory of quantum electrodynamics is mathematically self-consistent. It's surprising that the theory still hasn't been proved self-consistent one way or the other by now; I suspect that renormalization is not mathematically legitimate.
Feynman was concerned that all field theories known in the 1960s had the property that the interactions become infinitely strong at short enough distance scales. This property called a Landau pole, made it plausible that quantum field theories were all inconsistent. In 1974, Gross, Politzer and Wilczek showed that another quantum field theory, quantum chromodynamics, does not have a Landau pole. Feynman, along with most others, accepted that QCD was a fully consistent theory.[citation needed]
The general unease was almost universal in texts up to the 1970s and 1980s. Beginning in the 1970s, however, inspired by work on the renormalization group and effective field theory, and despite the fact that Dirac and various others—all of whom belonged to the older generation—never withdrew their criticisms, attitudes began to change, especially among younger theorists. Kenneth G. Wilson and others demonstrated that the renormalization group is useful in statistical field theory applied to condensed matter physics, where it provides important insights into the behavior of phase transitions. In condensed matter physics, a physical short-distance regulator exists: matter ceases to be continuous on the scale of atoms. Short-distance divergences in condensed matter physics do not present a philosophical problem since the field theory is only an effective, smoothed-out representation of the behavior of matter anyway; there are no infinities since the cutoff is always finite, and it makes perfect sense that the bare quantities are cutoff-dependent.
If QFT holds all the way down past the Planck length (where it might yield to string theory, causal set theory or something different), then there may be no real problem with short-distance divergences in particle physics either; all field theories could simply be effective field theories. In a sense, this approach echoes the older attitude that the divergences in QFT speak of human ignorance about the workings of nature, but also acknowledges that this ignorance can be quantified and that the resulting effective theories remain useful.
Be that as it may, Salam's remark[29] in 1972 seems still relevant
- Field-theoretic infinities – first encountered in Lorentz's computation of electron self-mass – have persisted in classical electrodynamics for seventy and in quantum electrodynamics for some thirty-five years. These long years of frustration have left in the subject a curious affection for the infinities and a passionate belief that they are an inevitable part of nature; so much so that even the suggestion of a hope that they may, after all, be circumvented — and finite values for the renormalization constants computed – is considered irrational. Compare Russell's postscript to the third volume of his autobiography The Final Years, 1944–1969 (George Allen and Unwin, Ltd., London 1969),[30] p. 221:
- In the modern world, if communities are unhappy, it is often because they have ignorances, habits, beliefs, and passions, which are dearer to them than happiness or even life. I find many men in our dangerous age who seem to be in love with misery and death, and who grow angry when hopes are suggested to them. They think hope is irrational and that, in sitting down to lazy despair, they are merely facing facts.
In QFT, the value of a physical constant, in general, depends on the scale that one chooses as the renormalization point, and it becomes very interesting to examine the renormalization group running of physical constants under changes in the energy scale. The coupling constants in the Standard Model of particle physics vary in different ways with increasing energy scale: the coupling of quantum chromodynamics and the weak isospin coupling of the electroweak force tend to decrease, and the weak hypercharge coupling of the electroweak force tends to increase. At the colossal energy scale of 1015 GeV (far beyond the reach of our current particle accelerators), they all become approximately the same size (Grotz and Klapdor 1990, p. 254), a major motivation for speculations about grand unified theory. Instead of being only a worrisome problem, renormalization has become an important theoretical tool for studying the behavior of field theories in different regimes.
If a theory featuring renormalization (e.g. QED) can only be sensibly interpreted as an effective field theory, i.e. as an approximation reflecting human ignorance about the workings of nature, then the problem remains of discovering a more accurate theory that does not have these renormalization problems. As Lewis Ryder has put it, "In the Quantum Theory, these [classical] divergences do not disappear; on the contrary, they appear to get worse. And despite the comparative success of renormalisation theory, the feeling remains that there ought to be a more satisfactory way of doing things."[31]
Renormalizability
From this philosophical reassessment, a new concept follows naturally: the notion of renormalizability. Not all theories lend themselves to renormalization in the manner described above, with a finite supply of counterterms and all quantities becoming cutoff-independent at the end of the calculation. If the Lagrangian contains combinations of field operators of high enough dimension in energy units, the counterterms required to cancel all divergences proliferate to infinite number, and, at first glance, the theory would seem to gain an infinite number of free parameters and therefore lose all predictive power, becoming scientifically worthless. Such theories are called nonrenormalizable.
The Standard Model of particle physics contains only renormalizable operators, but the interactions of general relativity become nonrenormalizable operators if one attempts to construct a field theory of quantum gravity in the most straightforward manner (treating the metric in the Einstein–Hilbert Lagrangian as a perturbation about the Minkowski metric), suggesting that perturbation theory is not satisfactory in application to quantum gravity.
However, in an effective field theory, "renormalizability" is, strictly speaking, a misnomer. In nonrenormalizable effective field theory, terms in the Lagrangian do multiply to infinity, but have coefficients suppressed by ever-more-extreme inverse powers of the energy cutoff. If the cutoff is a real, physical quantity—that is, if the theory is only an effective description of physics up to some maximum energy or minimum distance scale—then these additional terms could represent real physical interactions. Assuming that the dimensionless constants in the theory do not get too large, one can group calculations by inverse powers of the cutoff, and extract approximate predictions to finite order in the cutoff that still have a finite number of free parameters. It can even be useful to renormalize these "nonrenormalizable" interactions.
Nonrenormalizable interactions in effective field theories rapidly become weaker as the energy scale becomes much smaller than the cutoff. The classic example is the Fermi theory of the weak nuclear force, a nonrenormalizable effective theory whose cutoff is comparable to the mass of the W particle. This fact may also provide a possible explanation for why almost all of the particle interactions we see are describable by renormalizable theories. It may be that any others that may exist at the GUT or Planck scale simply become too weak to detect in the realm we can observe, with one exception: gravity, whose exceedingly weak interaction is magnified by the presence of the enormous masses of stars and planets.[citation needed]
Renormalization schemes
In actual calculations, the counterterms introduced to cancel the divergences in Feynman diagram calculations beyond tree level must be fixed using a set of renormalisation conditions. The common renormalization schemes in use include:
- Minimal subtraction (MS) scheme and the related modified minimal subtraction (MS-bar) scheme
- On-shell scheme
Besides, there exists a "natural" definition of the renormalized coupling (combined with the photon propagator) as a propagator of dual free bosons, which does not explicitly require introducing the counterterms. [32]
Renormalization in statistical physics
History
A deeper understanding of the physical meaning and generalization of the renormalization process, which goes beyond the dilatation group of conventional renormalizable theories, came from condensed matter physics. Leo P. Kadanoff's paper in 1966 proposed the "block-spin" renormalization group.[33] The blocking idea is a way to define the components of the theory at large distances as aggregates of components at shorter distances.
This approach covered the conceptual point and was given full computational substance[22] in the extensive important contributions of Kenneth Wilson. The power of Wilson's ideas was demonstrated by a constructive iterative renormalization solution of a long-standing problem, the Kondo problem, in 1974, as well as the preceding seminal developments of his new method in the theory of second-order phase transitions and critical phenomena in 1971. He was awarded the Nobel prize for these decisive contributions in 1982.
Principles
In more technical terms, let us assume that we have a theory described by a certain function of the state variables and a certain set of coupling constants . This function may be a partition function, an action, a Hamiltonian, etc. It must contain the whole description of the physics of the system.
Now we consider a certain blocking transformation of the state variables , the number of must be lower than the number of . Now let us try to rewrite the function only in terms of the . If this is achievable by a certain change in the parameters, , then the theory is said to be renormalizable.
The possible
macroscopic states of the system, at a large scale, are given by this
set of fixed points.
Renormalization group fixed points
The most important information in the RG flow is its fixed points. A fixed point is defined by the vanishing of the beta function associated to the flow. Then, fixed points of the renormalization group are by definition scale invariant. In many cases of physical interest scale invariance enlarges to conformal invariance. One then has a conformal field theory at the fixed point.
The ability of several theories to flow to the same fixed point leads to universality.
If these fixed points correspond to free field theory, the theory is said to exhibit quantum triviality. Numerous fixed points appear in the study of lattice Higgs theories, but the nature of the quantum field theories associated with these remains an open question.[34]
See also
References
- ↑ See e.g., Weinberg vol I, chapter 10.
- ↑ Sanyuk, Valerii I.; Sukhanov, Alexander D. (2003-09-01). "Dirac in 20th century physics: a centenary assessment" (in en). Physics-Uspekhi 46 (9): 937–956. ISSN 1063-7869. https://ufn.ru/en/articles/2003/9/c/.
- ↑ Kar, Arnab (2014). Renormalization from Classical to Quantum Physics (Thesis). University of Rochester.
- ↑ Kramers presented his work at the 1947 Shelter Island Conference, repeated in 1948 at the Solvay Conference. The latter did not appear in print until the Proceedings of the Solvay Conference, published in 1950 (see Laurie M. Brown (ed.), Renormalization: From Lorentz to Landau (and Beyond), Springer, 2012, p. 53). Kramers' approach was nonrelativistic (see Jagdish Mehra, Helmut Rechenberg, The Conceptual Completion and Extensions of Quantum Mechanics 1932–1941. Epilogue: Aspects of the Further Development of Quantum Theory 1942–1999: Volumes 6, Part 2, Springer, 2001, p. 1050).
- ↑ H. Bethe (1947). "The Electromagnetic Shift of Energy Levels". Physical Review 72 (4): 339–341. doi:10.1103/PhysRev.72.339. Bibcode: 1947PhRv...72..339B.
- ↑ Schwinger, J. (1948). "On quantum-electrodynamics and the magnetic moment of the electron". Physical Review 73 (4): 416–417. doi:10.1103/PhysRev.73.416. Bibcode: 1948PhRv...73..416S.
- ↑ Schwinger, J. (1948). "I. A covariant formulation". Physical Review. Quantum Electrodynamics 74 (10): 1439–1461. doi:10.1103/PhysRev.74.1439. Bibcode: 1948PhRv...74.1439S.
- ↑ Schwinger, J. (1949). "II. Vacuum polarization and self-energy". Physical Review. Quantum Electrodynamics 75 (4): 651–679. doi:10.1103/PhysRev.75.651. Bibcode: 1949PhRv...75..651S.
- ↑ Schwinger, J. (1949). "III. The electromagnetic properties of the electron radiative corrections to scattering". Physical Review. Quantum Electrodynamics 76 (6): 790–817. doi:10.1103/PhysRev.76.790. Bibcode: 1949PhRv...76..790S.
- ↑ Feynman, Richard P. (1948). "Space-time approach to non-relativistic quantum mechanics". Reviews of Modern Physics 20 (2): 367–387. doi:10.1103/RevModPhys.20.367. Bibcode: 1948RvMP...20..367F. https://authors.library.caltech.edu/47756/1/FEYrmp48.pdf.
- ↑ Feynman, Richard P. (1948). "A relativistic cut-off for classical electrodynamics". Physical Review 74 (8): 939–946. doi:10.1103/PhysRev.74.939. Bibcode: 1948PhRv...74..939F. https://authors.library.caltech.edu/3516/1/FEYpr48a.pdf.
- ↑ Feynman, Richard P. (1948). "A relativistic cut-off for quantum electrodynamics". Physical Review 74 (10): 1430–1438. doi:10.1103/PhysRev.74.1430. Bibcode: 1948PhRv...74.1430F. https://authors.library.caltech.edu/3517/1/FEYpr48b.pdf.
- ↑ Tomonaga, S. (1946-08-01). "On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields". Progress of Theoretical Physics (Oxford University Press (OUP)) 1 (2): 27–42. doi:10.1143/ptp.1.27. ISSN 1347-4081. Bibcode: 1946PThPh...1...27T.
- ↑ Koba, Z.; Tati, T.; Tomonaga, S.-i. (1947-10-01). "On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields. II: Case of Interacting Electromagnetic and Electron Fields". Progress of Theoretical Physics (Oxford University Press (OUP)) 2 (3): 101–116. doi:10.1143/ptp/2.3.101. ISSN 0033-068X. Bibcode: 1947PThPh...2..101K.
- ↑ Koba, Z.; Tati, T.; Tomonaga, S.-i. (1947-12-01). "On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields. III: Case of Interacting Electromagnetic and Electron Fields". Progress of Theoretical Physics (Oxford University Press (OUP)) 2 (4): 198–208. doi:10.1143/ptp/2.4.198. ISSN 0033-068X. Bibcode: 1947PThPh...2..198K.
- ↑ Kanesawa, S.; Tomonaga, S.-i. (1948-03-01). "On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields. [IV]: Case of Interacting Electromagnetic and Meson Fields". Progress of Theoretical Physics (Oxford University Press (OUP)) 3 (1): 1–13. doi:10.1143/ptp/3.1.1. ISSN 0033-068X.
- ↑ Kanesawa, S.; Tomonaga, S.-i. (1948-06-01). "On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields V: Case of Interacting Electromagnetic and Meson Fields". Progress of Theoretical Physics (Oxford University Press (OUP)) 3 (2): 101–113. doi:10.1143/ptp/3.2.101. ISSN 0033-068X. Bibcode: 1948PThPh...3..101K.
- ↑ Koba, Z.; Tomonaga, S.-i. (1948-09-01). "On Radiation Reactions in Collision Processes. I: Application of the "Self-Consistent" Subtraction Method to the Elastic Scattering of an Electron". Progress of Theoretical Physics (Oxford University Press (OUP)) 3 (3): 290–303. doi:10.1143/ptp/3.3.290. ISSN 0033-068X. Bibcode: 1948PThPh...3..290K.
- ↑ Tomonaga, Sin-Itiro; Oppenheimer, J. R. (1948-07-15). "On Infinite Field Reactions in Quantum Field Theory". Physical Review (American Physical Society (APS)) 74 (2): 224–225. doi:10.1103/physrev.74.224. ISSN 0031-899X. Bibcode: 1948PhRv...74..224T.
- ↑ Dyson, F. J. (1949). "The radiation theories of Tomonaga, Schwinger, and Feynman". Phys. Rev. 75 (3): 486–502. doi:10.1103/PhysRev.75.486. Bibcode: 1949PhRv...75..486D.
- ↑ Peskin, Michael E.; Schroeder, Daniel V. (1995). An Introduction to Quantum Field Theory. Reading: Addison-Wesley. Chapter 10. ISBN 9780201503975. https://archive.org/details/introductiontoqu0000pesk.
- ↑ 22.0 22.1 Wilson, Kenneth G. (1975-10-01). "The renormalization group: Critical phenomena and the Kondo problem". Reviews of Modern Physics (American Physical Society (APS)) 47 (4): 773–840. doi:10.1103/revmodphys.47.773. ISSN 0034-6861. Bibcode: 1975RvMP...47..773W.
- ↑ 't Hooft, G.; Veltman, M. (1972). "Regularization and renormalization of gauge fields". Nuclear Physics B 44 (1): 189–213. doi:10.1016/0550-3213(72)90279-9. Bibcode: 1972NuPhB..44..189T. https://repositorio.unal.edu.co/handle/unal/81144.
- ↑ Dyson, F. J. (1952-02-15). "Divergence of Perturbation Theory in Quantum Electrodynamics". Physical Review (American Physical Society (APS)) 85 (4): 631–632. doi:10.1103/physrev.85.631. ISSN 0031-899X. Bibcode: 1952PhRv...85..631D.
- ↑ Stern, A. W. (1952-11-07). "Space, Field, and Ether in Contemporary Physics". Science (American Association for the Advancement of Science (AAAS)) 116 (3019): 493–496. doi:10.1126/science.116.3019.493. ISSN 0036-8075. PMID 17801299. Bibcode: 1952Sci...116..493S.
- ↑ P.A.M. Dirac, "The Evolution of the Physicist's Picture of Nature", in Scientific American, May 1963, p. 53.
- ↑ Kragh, Helge; Dirac: A scientific biography, CUP 1990, p. 184
- ↑ Feynman, Richard P.; QED: The Strange Theory of Light and Matter, Penguin 1990, p. 128
- ↑ Isham, C. J.; Salam, Abdus; Strathdee, J. (1972-05-15). "Infinity Suppression in Gravity-Modified Electrodynamics. II". Physical Review D (American Physical Society (APS)) 5 (10): 2548–2565. doi:10.1103/physrevd.5.2548. ISSN 0556-2821. Bibcode: 1972PhRvD...5.2548I.
- ↑ Russell, Bertrand. The Autobiography of Bertrand Russell: The Final Years, 1944-1969 (Bantam Books, 1970)
- ↑ Ryder, Lewis. Quantum Field Theory, page 390 (Cambridge University Press 1996).
- ↑ Makogon, D.; Morais Smith, C. (2022). "Median-point approximation and its application for the study of fermionic systems". Phys. Rev. B 105 (17): 174505. doi:10.1103/PhysRevB.105.174505. Bibcode: 2022PhRvB.105q4505M.
- ↑ L.P. Kadanoff (1966): "Scaling laws for Ising models near ", Physics (Long Island City, N.Y.) 2, 263.
- ↑ D. J. E. Callaway (1988). "Triviality Pursuit: Can Elementary Scalar Particles Exist?". Physics Reports 167 (5): 241–320. doi:10.1016/0370-1573(88)90008-7.
Further reading
General introduction
- DeDeo, Simon; Introduction to Renormalization (2017). Santa Fe Institute Complexity Explorer MOOC. Renormalization from a complex systems point of view, including Markov Chains, Cellular Automata, the real space Ising model, the Krohn-Rhodes Theorem, QED, and rate distortion theory.
- Delamotte, Bertrand (2004). "A hint of renormalization". American Journal of Physics 72 (2): 170–184. doi:10.1119/1.1624112. Bibcode: 2004AmJPh..72..170D.
- Baez, John; Renormalization Made Easy, (2005). A qualitative introduction to the subject.
- Blechman, Andrew E.; Renormalization: Our Greatly Misunderstood Friend, (2002). Summary of a lecture; has more information about specific regularization and divergence-subtraction schemes.
- Cao, Tian Yu; Schweber, Silvan S. (1993). "The conceptual foundations and the philosophical aspects of renormalization theory". Synthese 97: 33–108. doi:10.1007/BF01255832.
- Shirkov, Dmitry; Fifty Years of the Renormalization Group, C.E.R.N. Courrier 41(7) (2001). Full text available at : I.O.P Magazines.
- E. Elizalde; Zeta regularization techniques with Applications.
Mainly: quantum field theory
- N. N. Bogoliubov, D. V. Shirkov (1959): The Theory of Quantized Fields. New York, Interscience. The first text-book on the renormalization group theory.
- Ryder, Lewis H.; Quantum Field Theory (Cambridge University Press, 1985), ISBN 0-521-33859-X Highly readable textbook, certainly the best introduction to relativistic Q.F.T. for particle physics.
- Zee, Anthony; Quantum Field Theory in a Nutshell, Princeton University Press (2003) ISBN 0-691-01019-6. Another excellent textbook on Q.F.T.
- Weinberg, Steven; The Quantum Theory of Fields (3 volumes) Cambridge University Press (1995). A monumental treatise on Q.F.T. written by a leading expert, Nobel laureate 1979.
- Pokorski, Stefan; Gauge Field Theories, Cambridge University Press (1987) ISBN 0-521-47816-2.
- 't Hooft, Gerard; The Glorious Days of Physics – Renormalization of Gauge theories, lecture given at Erice (August/September 1998) by the Nobel laureate 1999 . Full text available at: hep-th/9812203.
- Rivasseau, Vincent; An introduction to renormalization, Poincaré Seminar (Paris, Oct. 12, 2002), published in : Duplantier, Bertrand; Rivasseau, Vincent (Eds.); Poincaré Seminar 2002, Progress in Mathematical Physics 30, Birkhäuser (2003) ISBN 3-7643-0579-7. Full text available in PostScript.
- Rivasseau, Vincent; From perturbative to constructive renormalization, Princeton University Press (1991) ISBN 0-691-08530-7. Full text available in PostScript[yes|permanent dead link|dead link}}] and in PDF (draft version).
- Iagolnitzer, Daniel & Magnen, J.; Renormalization group analysis, Encyclopaedia of Mathematics, Kluwer Academic Publisher (1996). Full text available in PostScript and pdf here.
- Scharf, Günter; Finite quantum electrodynamics: The causal approach, Springer Verlag Berlin Heidelberg New York (1995) ISBN 3-540-60142-2.
- A. S. Švarc (Albert Schwarz), Математические основы квантовой теории поля, (Mathematical aspects of quantum field theory), Atomizdat, Moscow, 1975. 368 pp.
Mainly: statistical physics
- A. N. Vasil'ev; The Field Theoretic Renormalization Group in Critical Behavior Theory and Stochastic Dynamics (Routledge Chapman & Hall 2004); ISBN 978-0-415-31002-4
- Nigel Goldenfeld; Lectures on Phase Transitions and the Renormalization Group, Frontiers in Physics 85, Westview Press (June, 1992) ISBN 0-201-55409-7. Covering the elementary aspects of the physics of phases transitions and the renormalization group, this popular book emphasizes understanding and clarity rather than technical manipulations.
- Zinn-Justin, Jean; Quantum Field Theory and Critical Phenomena, Oxford University Press (4th edition – 2002) ISBN 0-19-850923-5. A masterpiece on applications of renormalization methods to the calculation of critical exponents in statistical mechanics, following Wilson's ideas (Kenneth Wilson was Nobel laureate 1982).
- Zinn-Justin, Jean; Phase Transitions & Renormalization Group: from Theory to Numbers, Poincaré Seminar (Paris, Oct. 12, 2002), published in : Duplantier, Bertrand; Rivasseau, Vincent (Eds.); Poincaré Seminar 2002, Progress in Mathematical Physics 30, Birkhäuser (2003) ISBN 3-7643-0579-7. Full text available in PostScript .
- Domb, Cyril; The Critical Point: A Historical Introduction to the Modern Theory of Critical Phenomena, CRC Press (March, 1996) ISBN 0-7484-0435-X.
- Brown, Laurie M. (Ed.); Renormalization: From Lorentz to Landau (and Beyond), Springer-Verlag (New York-1993) ISBN 0-387-97933-6.
- Cardy, John; Scaling and Renormalization in Statistical Physics, Cambridge University Press (1996) ISBN 0-521-49959-3.
Miscellaneous
- Shirkov, Dmitry; The Bogoliubov Renormalization Group, JINR Communication E2-96-15 (1996). Full text available at: hep-th/9602024
- Zinn-Justin, Jean; Renormalization and renormalization group: From the discovery of UV divergences to the concept of effective field theories, in: de Witt-Morette C., Zuber J.-B. (eds), Proceedings of the NATO ASI on Quantum Field Theory: Perspective and Prospective, June 15–26, 1998, Les Houches, France, Kluwer Academic Publishers, NATO ASI Series C 530, 375–388 (1999). Full text available in PostScript.
- Connes, Alain; Symétries Galoisiennes & Renormalisation, Poincaré Seminar (Paris, Oct. 12, 2002), published in : Duplantier, Bertrand; Rivasseau, Vincent (Eds.); Poincaré Seminar 2002, Progress in Mathematical Physics 30, Birkhäuser (2003) ISBN 3-7643-0579-7. French mathematician Alain Connes (Fields medallist 1982) describe the mathematical underlying structure (the Hopf algebra) of renormalization, and its link to the Riemann-Hilbert problem. Full text (in French) available at arXiv:math/0211199.
External links
 |
