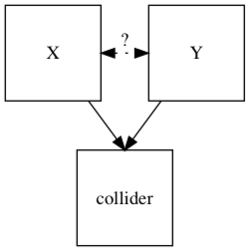
Collider (epidemiology)

In statistics and causal graphs, a variable is a collider when it is causally influenced by two or more variables. The causal variables influencing the collider are themselves not necessarily associated. The name "collider" reflects the fact that in graphical models, the arrow heads from variables that lead into the collider appear to "collide" on the node that is the collider. They are sometimes also referred to as inverted forks.

Figure 1: SEM model of a Collider

The result of having a collider in the path is that the collider blocks the association between the variables that influence it. Thus, the collider does not generate an unconditional association between the variables that determine it.

Conditioning on the collider via regression analysis, stratification, experimental design, or sample selection based on values of the collider create a non-causal association between X and Y (Berkson's paradox). In the terminology of causal graphs, conditioning on the colllider open the path between X and Y. This will introduce bias when estimating the causal association between X and Y, potentially introducing associations where there are none. Colliders can therefore undermine attempts to test causal theories.

Colliders are sometimes confused with confounder variables. Unlike colliders, confounder variables should be controlled for when estimating causal associations.

See also

• Causality
• Causal graphs
• Confounding
• Directed acyclic graph
• Selection bias
• Path analysis