Colpitts oscillator

Short description: LC oscillator design

A Colpitts oscillator, invented in 1918 by Canadian-American engineer Edwin H. Colpitts using vacuum tubes, is one of a number of designs for LC oscillators, electronic oscillators that use a combination of inductors (L) and capacitors (C) to produce an oscillation at a certain frequency. The distinguishing feature of the Colpitts oscillator is that the feedback for the active device is taken from a voltage divider made of two capacitors in series across the inductor.

Overview

Figure 1: Simple common-base Colpitts oscillator (with simplified biasing)

Figure 2: Simple common-collector Colpitts oscillator (with simplified biasing)

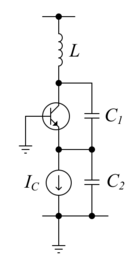
The Colpitts circuit, like other LC oscillators, consists of a gain device (such as a bipolar junction transistor, field-effect transistor, operational amplifier, or vacuum tube) with its output connected to its input in a feedback loop containing a parallel LC circuit (tuned circuit), which functions as a bandpass filter to set the frequency of oscillation. The amplifier will have differing input and output impedances, and these need to be coupled into the LC circuit without overly damping it.

A Colpitts oscillator uses a pair of capacitors to provide voltage division to couple the energy in and out of the tuned circuit. (It can be considered as the electrical dual of a Hartley oscillator, where the feedback signal is taken from an "inductive" voltage divider consisting of two coils in series (or a tapped coil).) Fig. 1 shows the common-base Colpitts circuit. The inductor L and the series combination of C₁ and C₂ form the resonant tank circuit, which determines the frequency of the oscillator. The voltage across C₂ is applied to the base-emitter junction of the transistor, as feedback to create oscillations. Fig. 2 shows the common-collector version. Here the voltage across C₁ provides feedback. The frequency of oscillation is approximately the resonant frequency of the LC circuit, which is the series combination of the two capacitors in parallel with the inductor:

[math]\displaystyle{ f_0 = \frac{1}{2\pi \sqrt{L \frac{C_1 C_2}{C_1 + C_2}}}. }[/math]

The actual frequency of oscillation will be slightly lower due to junction capacitances and resistive loading of the transistor.

As with any oscillator, the amplification of the active component should be marginally larger than the attenuation of the resonator losses and its voltage division, to obtain stable operation. Thus, a Colpitts oscillator used as a variable-frequency oscillator (VFO) performs best when a variable inductance is used for tuning, as opposed to tuning just one of the two capacitors. If tuning by variable capacitor is needed, it should be done with a third capacitor connected in parallel to the inductor (or in series as in the Clapp oscillator).

Practical example

Figure 3: Practical common-base Colpitts oscillator with an oscillation frequency of ~50 MHz

Fig. 3 shows a working example with component values. Instead of bipolar junction transistors, other active components such as field-effect transistors or vacuum tubes, capable of producing gain at the desired frequency, could be used.

The capacitor at the base provides an AC path to ground for parasitic inductances that could lead to unwanted resonance at undesired frequencies. Selection of the base's biasing resistors is not trivial. Periodic oscillation starts for a critical bias current and with the variation of the bias current to a higher value chaotic oscillations are observed.

Theory

Ideal Colpitts oscillator model (common-collector configuration)

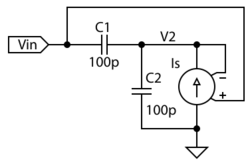
One method of oscillator analysis is to determine the input impedance of an input port neglecting any reactive components. If the impedance yields a negative resistance term, oscillation is possible. This method will be used here to determine conditions of oscillation and the frequency of oscillation.

An ideal model is shown to the right. This configuration models the common collector circuit in the section above. For initial analysis, parasitic elements and device non-linearities will be ignored. These terms can be included later in a more rigorous analysis. Even with these approximations, acceptable comparison with experimental results is possible.

Ignoring the inductor, the input impedance at the base can be written as

[math]\displaystyle{ Z_\text{in} = \frac{v_1}{i_1}, }[/math]

where [math]\displaystyle{ v_1 }[/math] is the input voltage, and [math]\displaystyle{ i_1 }[/math] is the input current. The voltage [math]\displaystyle{ v_2 }[/math] is given by

[math]\displaystyle{ v_2 = i_2 Z_2, }[/math]

where [math]\displaystyle{ Z_2 }[/math] is the impedance of [math]\displaystyle{ C_2 }[/math]. The current flowing into [math]\displaystyle{ C_2 }[/math] is [math]\displaystyle{ i_2 }[/math], which is the sum of two currents:

[math]\displaystyle{ i_2 = i_1 + i_s, }[/math]

where [math]\displaystyle{ i_s }[/math] is the current supplied by the transistor. [math]\displaystyle{ i_s }[/math] is a dependent current source given by

[math]\displaystyle{ i_s = g_m (v_1 - v_2), }[/math]

where [math]\displaystyle{ g_m }[/math] is the transconductance of the transistor. The input current [math]\displaystyle{ i_1 }[/math] is given by

[math]\displaystyle{ i_1 = \frac{v_1 - v_2}{Z_1}, }[/math]

where [math]\displaystyle{ Z_1 }[/math] is the impedance of [math]\displaystyle{ C_1 }[/math]. Solving for [math]\displaystyle{ v_2 }[/math] and substituting above yields

[math]\displaystyle{ Z_\text{in} = Z_1 + Z_2 + g_m Z_1 Z_2. }[/math]

The input impedance appears as the two capacitors in series with the term [math]\displaystyle{ R_\text{in} }[/math], which is proportional to the product of the two impedances:

[math]\displaystyle{ R_\text{in} = g_m Z_1 Z_2. }[/math]

If [math]\displaystyle{ Z_1 }[/math] and [math]\displaystyle{ Z_2 }[/math] are complex and of the same sign, then [math]\displaystyle{ R_\text{in} }[/math] will be a negative resistance. If the impedances for [math]\displaystyle{ Z_1 }[/math] and [math]\displaystyle{ Z_2 }[/math] are substituted, [math]\displaystyle{ R_\text{in} }[/math] is

[math]\displaystyle{ R_\text{in} = \frac{-g_m}{\omega^2 C_1 C_2}. }[/math]

If an inductor is connected to the input, then the circuit will oscillate if the magnitude of the negative resistance is greater than the resistance of the inductor and any stray elements. The frequency of oscillation is as given in the previous section.

For the example oscillator above, the emitter current is roughly 1 mA. The transconductance is roughly 40 mS. Given all other values, the input resistance is roughly

[math]\displaystyle{ R_\text{in} = -30\ \Omega. }[/math]

This value should be sufficient to overcome any positive resistance in the circuit. By inspection, oscillation is more likely for larger values of transconductance and smaller values of capacitance. A more complicated analysis of the common-base oscillator reveals that a low-frequency amplifier voltage gain must be at least 4 to achieve oscillation. The low-frequency gain is given by

[math]\displaystyle{ A_v = g_m R_p \ge 4. }[/math]

Comparison of Hartley and Colpitts oscillators

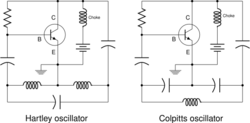
If the two capacitors are replaced by inductors, and magnetic coupling is ignored, the circuit becomes a Hartley oscillator. In that case, the input impedance is the sum of the two inductors and a negative resistance given by

[math]\displaystyle{ R_\text{in} = -g_m \omega^2 L_1 L_2. }[/math]

In the Hartley circuit, oscillation is more likely for larger values of transconductance and larger values of inductance.

The above analysis also describes the behavior of the Pierce oscillator. The Pierce oscillator, with two capacitors and one inductor, is equivalent to the Colpitts oscillator. Equivalence can be shown by choosing the junction of the two capacitors as the ground point. An electrical dual of the standard Pierce oscillator using two inductors and one capacitor is equivalent to the Hartley oscillator.

Working Principle

A Colpitts oscillator is an electronic circuit that generates a sinusoidal waveform, typically in the radio frequency range. It uses an inductor and two capacitors in parallel to form a resonant tank circuit, which determines the oscillation frequency. The output signal from the tank circuit is fed back into the input of an amplifier, where it is amplified and fed back into the tank circuit. The feedback signal provides the necessary phase shift for sustained oscillation.

The working principle of a Colpitts oscillator can be explained as follows:

• When the power supply is switched on, the capacitors C1 and C2 start charging through the resistor R1 and R2. The voltage across C2 is coupled to the base of the transistor through the capacitor Cin.
• The transistor amplifies the input signal and produces an inverted output signal at the collector. The output signal is coupled to the tank circuit through the capacitor Cout.
• The tank circuit resonates at its natural frequency, which is given by:

f=2πLCt1

Where:

• f = frequency of oscillation
• L = inductance of the inductor
• Ct = total capacitance of the series combination of C1 and C2, given by:

Ct=C1+C2C1C2

• The resonant frequency is independent of the values of C1 and C2, but depends on their ratio. The ratio of C1 and C2 also affects the feedback gain and the stability of the oscillator.
• The voltage across the inductor L is in phase with the voltage across C2, and 180 degrees out of phase with the voltage across C1. Therefore, the voltage at the junction of C1 and C2 is 180 degrees out of phase with the voltage at the collector of the transistor. This voltage is fed back to the base of the transistor through Cin, providing another 180 degrees phase shift. Thus, the total phase shift around the loop is 360 degrees, which is equivalent to zero degrees. This satisfies the Barkhausen criterion for oscillation.
• The amplitude of the oscillation depends on the feedback gain and the losses in the tank circuit. The feedback gain should be equal to or slightly greater than the losses for sustained oscillation. The feedback gain can be adjusted by varying the values of R1 and R2, or by using a variable capacitor in place of C1 or C2.

The Colpitts oscillator is widely used in various applications, such as RF communication systems, signal generators, and electronic testing equipment. It has better frequency stability than the Hartley oscillator, which uses a tapped inductor instead of a tapped capacitor in the tank circuit. However, the Colpitts oscillator may require a higher supply voltage and a larger coupling capacitor than the Hartley oscillator.

Oscillation amplitude

The amplitude of oscillation is generally difficult to predict, but it can often be accurately estimated using the describing function method.

For the common-base oscillator in Figure 1, this approach applied to a simplified model predicts an output (collector) voltage amplitude given by

[math]\displaystyle{ V_C = 2 I_C R_L \frac{C_2}{C_1 + C_2}, }[/math]

where [math]\displaystyle{ I_C }[/math] is the bias current, and [math]\displaystyle{ R_L }[/math] is the load resistance at the collector.

This assumes that the transistor does not saturate, the collector current flows in narrow pulses, and that the output voltage is sinusoidal (low distortion).

This approximate result also applies to oscillators employing different active device, such as MOSFETs and vacuum tubes.

Further reading

• Lee, T. (December 2003). The Design of CMOS Radio-Frequency Integrated Circuits. Cambridge University Press. ISBN 978-0521835398. 
• Rohde, Ulrich L.; Poddar, Ajay K.; Böck, Georg (May 2005). The Design of Modern Microwave Oscillators for Wireless Applications. New York, NY: John Wiley & Sons. ISBN 0-471-72342-8. .
• Vendelin, George; Pavio, Anthony M.; Rohde, Ulrich L. (May 2005). Microwave Circuit Design Using Linear and Nonlinear Techniques. New York, NY: John Wiley & Sons. ISBN 0-471-41479-4. .
• Rohde, Ulrich L.; Apte, Anisha M. (August 2016). "Everything You Always Wanted to Know About Colpitts Oscillators". IEEE Microwave Magazine 17 (6): 59–76. doi:10.1109/MMM.2016.2561498. 
• Apte, Anisha M.; Poddar, Ajay K.; Rohde, Ulrich L.; Rubiola, Enrico (2016). "Colpitts oscillator: A new criterion of energy saving for high performance signal sources". IEEE International Frequency Control Symposium. doi:10.1109/FCS.2016.7546729.