Engineering:Electronic oscillator

From HandWiki
Short description: Type of electronic circuit
Simple relaxation oscillator made by feeding back an inverting Schmitt trigger's output voltage through a RC network to its input.

An electronic oscillator is an electronic circuit that produces a periodic, oscillating or alternating current (AC) signal, usually a sine wave, square wave or a triangle wave,[1][2][3] powered by a direct current (DC) source. Oscillators are found in many electronic devices, such as radio receivers, television sets, radio and television broadcast transmitters, computers, computer peripherals, cellphones, radar, and many other devices.[1]

Oscillators are often characterized by the frequency of their output signal:

  • A low-frequency oscillator (LFO) is an oscillator that generates a frequency below approximately 20 Hz. This term is typically used in the field of audio synthesizers, to distinguish it from an audio frequency oscillator.
  • An audio oscillator produces frequencies in the audio range, 20 Hz to 20 kHz.[2]
  • A radio frequency (RF) oscillator produces signals above the audio range, more generally in the range of 100 kHz to 100 GHz.[2]
Crystal oscillator

There are two general types of electronic oscillators: the linear or harmonic oscillator, and the nonlinear or relaxation oscillator.[2][4] The two types are fundamentally different in how oscillation is produced, as well as in the characteristic type of output signal that is generated.

The most-common linear oscillator in use is the crystal oscillator, in which the output frequency is controlled by a piezo-electric resonator consisting of a vibrating quartz crystal. Crystal oscillators are ubiquitous in modern electronics, being the source for the clock signal in computers and digital watches, as well as a source for the signals generated in radio transmitters and receivers. As a crystal oscillator’s “native” output waveform is sinusoidal, a signal-conditioning circuit may be used to convert the output to other waveform types, such as the square wave typically utilized in computer clock circuits.

Harmonic oscillators

Block diagram of a feedback linear oscillator; an amplifier A with its output vo fed back into its input vf through a filter, β(jω).

Linear or harmonic oscillators generate a sinusoidal (or nearly-sinusoidal) signal. There are two types:

Feedback oscillator

The most common form of linear oscillator is an electronic amplifier such as a transistor or operational amplifier connected in a feedback loop with its output fed back into its input through a frequency selective electronic filter to provide positive feedback. When the power supply to the amplifier is switched on initially, electronic noise in the circuit provides a non-zero signal to get oscillations started.[5]:p.113–114 The noise travels around the loop and is amplified and filtered until very quickly it converges on a sine wave at a single frequency.

Feedback oscillator circuits can be classified according to the type of frequency selective filter they use in the feedback loop:[2][4]

  • In an RC oscillator circuit, the filter is a network of resistors and capacitors.[2][4] RC oscillators are mostly used to generate lower frequencies, for example in the audio range. Common types of RC oscillator circuits are the phase shift oscillator and the Wien bridge oscillator. LR oscillators, using inductor and resistor filters also exist, however they are much less common due to the required size of an inductor to achieve a value appropriate for use at lower frequencies.

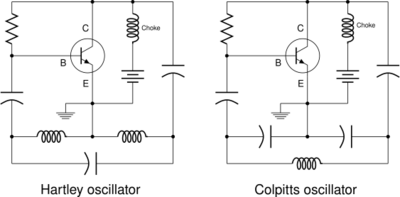
Two common LC oscillator circuits, the Hartley and Colpitts oscillators
  • In an LC oscillator circuit, the filter is a tuned circuit (often called a tank circuit) consisting of an inductor (L) and capacitor (C) connected together, which acts as a resonator.[2][4] Charge flows back and forth between the capacitor's plates through the inductor, so the tuned circuit can store electrical energy oscillating at its resonant frequency. The amplifier adds power to compensate for resistive energy losses in the circuit and supplies the power for the output signal. LC oscillators are often used at radio frequencies,[2] when a tunable frequency source is necessary, such as in signal generators, tunable radio transmitters and the local oscillators in radio receivers. Typical LC oscillator circuits are the Hartley, Colpitts[2] and Clapp circuits.
  • In a crystal oscillator circuit the filter is a piezoelectric crystal (commonly a quartz crystal).[2][4] The crystal mechanically vibrates as a resonator, and its frequency of vibration determines the oscillation frequency. Crystals have a very high Q-factor and also better temperature stability than tuned circuits, so crystal oscillators have much better frequency stability than LC or RC oscillators. Crystal oscillators are the most common type of linear oscillator, used to stabilize the frequency of most radio transmitters, and to generate the clock signal in computers and quartz clocks. Crystal oscillators often use the same circuits as LC oscillators, with the crystal replacing the tuned circuit;[2] the Pierce oscillator circuit is also commonly used. Quartz crystals are generally limited to frequencies of 30 MHz or below.[2] Other types of resonators, dielectric resonators and surface acoustic wave (SAW) devices, are used to control higher frequency oscillators, up into the microwave range. For example, SAW oscillators are used to generate the radio signal in cell phones.[6]

Negative-resistance oscillator

(left) Typical block diagram of a negative resistance oscillator. In some types the negative resistance device is connected in parallel with the resonant circuit. (right) A negative-resistance microwave oscillator consisting of a Gunn diode in a cavity resonator. The negative resistance of the diode excites microwave oscillations in the cavity, which radiate out the aperture into a waveguide.

In addition to the feedback oscillators described above, which use two-port amplifying active elements such as transistors and operational amplifiers, linear oscillators can also be built using one-port (two terminal) devices with negative resistance,[2][4] such as magnetron tubes, tunnel diodes, IMPATT diodes and Gunn diodes. Negative-resistance oscillators are usually used at high frequencies in the microwave range and above, since at these frequencies feedback oscillators perform poorly due to excessive phase shift in the feedback path.

In negative-resistance oscillators, a resonant circuit, such as an LC circuit, crystal, or cavity resonator, is connected across a device with negative differential resistance, and a DC bias voltage is applied to supply energy. A resonant circuit by itself is "almost" an oscillator; it can store energy in the form of electronic oscillations if excited, but because it has electrical resistance and other losses the oscillations are damped and decay to zero. The negative resistance of the active device cancels the (positive) internal loss resistance in the resonator, in effect creating a resonator with no damping, which generates spontaneous continuous oscillations at its resonant frequency.

The negative-resistance oscillator model is not limited to one-port devices like diodes; feedback oscillator circuits with two-port amplifying devices such as transistors and tubes also have negative resistance.[7][8][9] At high frequencies, three terminal devices such as transistors and FETs are also used in negative resistance oscillators. At high frequencies these devices do not need a feedback loop, but with certain loads applied to one port can become unstable at the other port and show negative resistance due to internal feedback. The negative resistance port is connected to a tuned circuit or resonant cavity, causing them to oscillate.[7][8][10] High-frequency oscillators in general are designed using negative-resistance techniques.[7][8][9]

List of harmonic oscillator circuits

Some of the many harmonic oscillator circuits are listed below:

Active devices used in oscillators and approximate maximum frequencies[8]
Device Frequency
Triode vacuum tube ~1 GHz
Bipolar transistor (BJT) ~20 GHz
Heterojunction bipolar transistor (HBT) ~50 GHz
Metal–semiconductor field-effect transistor (MESFET) ~100 GHz
Gunn diode, fundamental mode ~100 GHz
Magnetron tube ~100 GHz
High electron mobility transistor (HEMT) ~200 GHz
Klystron tube ~200 GHz
Gunn diode, harmonic mode ~200 GHz
IMPATT diode ~300 GHz
Gyrotron tube ~600 GHz

Relaxation oscillator

Main page: Engineering:Relaxation oscillator
A popular op-amp relaxation oscillator.

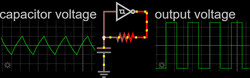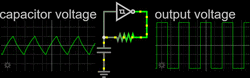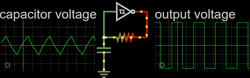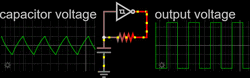
A nonlinear or relaxation oscillator produces a non-sinusoidal output, such as a square, sawtooth or triangle wave.[4] It consists of an energy-storing element (a capacitor or, more rarely, an inductor) and a nonlinear switching device (a latch, Schmitt trigger, or negative-resistance element) connected in a feedback loop. The switching device periodically charges and discharges the energy stored in the storage element thus causing abrupt changes in the output waveform.

Square-wave relaxation oscillators are used to provide the clock signal for sequential logic circuits such as timers and counters, although crystal oscillators are often preferred for their greater stability. Triangle-wave or sawtooth oscillators are used in the timebase circuits that generate the horizontal deflection signals for cathode ray tubes in analogue oscilloscopes and television sets. They are also used in voltage-controlled oscillators (VCOs), inverters and switching power supplies, dual-slope analog to digital converters (ADCs), and in function generators to generate square and triangle waves for testing equipment. In general, relaxation oscillators are used at lower frequencies and have poorer frequency stability than linear oscillators.

Ring oscillators are built of a ring of active delay stages. Generally the ring has an odd number of inverting stages, so that there is no single stable state for the internal ring voltages. Instead, a single transition propagates endlessly around the ring.

Some of the more common relaxation oscillator circuits are listed below:

Voltage-controlled oscillator (VCO)

Main page: Engineering:Voltage-controlled oscillator

An oscillator can be designed so that the oscillation frequency can be varied over some range by an input voltage or current. These voltage controlled oscillators are widely used in phase-locked loops, in which the oscillator's frequency can be locked to the frequency of another oscillator. These are ubiquitous in modern communications circuits, used in filters, modulators, demodulators, and forming the basis of frequency synthesizer circuits which are used to tune radios and televisions.

Radio frequency VCOs are usually made by adding a varactor diode to the tuned circuit or resonator in an oscillator circuit. Changing the DC voltage across the varactor changes its capacitance, which changes the resonant frequency of the tuned circuit. Voltage controlled relaxation oscillators can be constructed by charging and discharging the energy storage capacitor with a voltage controlled current source. Increasing the input voltage increases the rate of charging the capacitor, decreasing the time between switching events.

Theory of feedback oscillators

A feedback oscillator circuit consists of two parts connected in a feedback loop; an amplifier [math]\displaystyle{ A }[/math] and an electronic filter [math]\displaystyle{ \beta(j\omega) }[/math]. The filter's purpose is to limit the frequencies that can pass through the loop so the circuit only oscillates at the desired frequency.[11] Since the filter and wires in the circuit have resistance they consume energy and the amplitude of the signal drops as it passes through the filter. The amplifier is needed to increase the amplitude of the signal to compensate for the energy lost in the other parts of the circuit, so the loop will oscillate, as well as supply energy to the load attached to the output.

Frequency of oscillation - the Barkhausen criterion

Main page: Barkhausen stability criterion
To determine the loop gain, the feedback loop of the oscillator (left) is considered to be broken at some point (right).

To determine the frequency(s) [math]\displaystyle{ \omega_0\;=\;2\pi f_0 }[/math] at which a feedback oscillator circuit will oscillate, the feedback loop is thought of as broken at some point (see diagrams) to give an input and output port. A sine wave is applied to the input [math]\displaystyle{ v_i(t) = V_ie^{j\omega t} }[/math] and the amplitude and phase of the sine wave after going through the loop [math]\displaystyle{ v_o = V_o e^{j(\omega t + \phi)} }[/math] is calculated[12][13]

[math]\displaystyle{ v_o = A v_f\, }[/math]      and      [math]\displaystyle{ v_f = \beta(j\omega) v_i \, }[/math]      so      [math]\displaystyle{ v_o = A\beta(j\omega) v_i\, }[/math]

Since in the complete circuit [math]\displaystyle{ v_o }[/math] is connected to [math]\displaystyle{ v_i }[/math], for oscillations to exist

[math]\displaystyle{ v_o(t) = v_i(t) }[/math]

The ratio of output to input of the loop, [math]\displaystyle{ {v_o \over v_i} = A\beta(j\omega) }[/math], is called the loop gain. So the condition for oscillation is that the loop gain must be one[14]:p.3–5[13][15][16]

[math]\displaystyle{ A\beta(j\omega_0) = 1\, }[/math]

Since [math]\displaystyle{ A\beta(j\omega) }[/math] is a complex number with two parts, a magnitude and an angle, the above equation actually consists of two conditions:[17][16][13]

  • The magnitude of the gain (amplification) around the loop at ω0 must be unity
[math]\displaystyle{ |A||\beta(j\omega_0)| = 1\, \qquad\qquad\qquad\qquad\qquad\qquad \text{(1)} }[/math]
so that after a trip around the loop the sine wave is the same amplitude. It can be seen intuitively that if the loop gain were greater than one, the amplitude of the sinusoidal signal would increase as it travels around the loop, resulting in a sine wave that grows exponentially with time, without bound.[11] If the loop gain were less than one, the signal would decrease around the loop, resulting in an exponentially decaying sine wave that decreases to zero.
  • The sine wave at the end of the loop must be in phase with the wave at the beginning of the loop.[13] Since the sine wave is periodic and repeats every 2π radians, this means that the phase shift around the loop at the oscillation frequency ω0 must be zero or a multiple of 2π radians (360°)
[math]\displaystyle{ \angle A + \angle \beta = 2 \pi n \qquad n \in 0, 1, 2... \, \qquad\qquad \text{(2)} }[/math]

Equations (1) and (2) are called the Barkhausen stability criterion.[16][14]:p.3–5 It is a necessary but not a sufficient criterion for oscillation, so there are some circuits which satisfy these equations that will not oscillate. An equivalent condition often used instead of the Barkhausen condition is that the circuit's closed loop transfer function (the circuit's complex impedance at its output) have a pair of poles on the imaginary axis.

In general, the phase shift of the feedback network increases with increasing frequency so there are only a few discrete frequencies (often only one) which satisfy the second equation.[16][11] If the amplifier gain [math]\displaystyle{ A }[/math] is high enough that the loop gain is unity (or greater, see Startup section) at one of these frequencies, the circuit will oscillate at that frequency. Many amplifiers such as common-emitter transistor circuits are "inverting", meaning that their output voltage decreases when their input increases.[17][13] In these the amplifier provides 180° phase shift, so the circuit will oscillate at the frequency at which the feedback network provides the other 180° phase shift.[14]:p.3–5[13]

At frequencies well below the poles of the amplifying device, the amplifier will act as a pure gain [math]\displaystyle{ A }[/math], but if the oscillation frequency [math]\displaystyle{ \omega_0 }[/math] is near the amplifier's cutoff frequency [math]\displaystyle{ \omega_C }[/math], within [math]\displaystyle{ 0.1\omega_C }[/math], the active device can no longer be considered a 'pure gain', and it will contribute some phase shift to the loop.[14]:p.3–5[18]

An alternate mathematical stability test sometimes used instead of the Barkhausen criterion is the Nyquist stability criterion.[14]:p.6–7 This has a wider applicability than the Barkhausen, so it can identify some of the circuits which pass the Barkhausen criterion but do not oscillate.

Frequency stability

Temperature changes, aging, and manufacturing tolerances will cause component values to "drift" away from their designed values.[19][20] Changes in frequency determining components such as the tank circuit in LC oscillators will cause the oscillation frequency to change, so for a constant frequency these components must have stable values. How stable the oscillator's frequency is to other changes in the circuit, such as changes in values of other components, gain of the amplifier, the load impedance, or the supply voltage, is mainly dependent on the Q factor ("quality factor") of the feedback filter.[19] Since the amplitude of the output is constant due to the nonlinearity of the amplifier (see Startup section below), changes in component values cause changes in the phase shift [math]\displaystyle{ \phi\;=\;\angle A\beta(j\omega) }[/math] of the feedback loop. Since oscillation can only occur at frequencies where the phase shift is a multiple of 360°, [math]\displaystyle{ \phi\;=\;360n^\circ }[/math], shifts in component values cause the oscillation frequency [math]\displaystyle{ \omega_0 }[/math] to change to bring the loop phase back to 360n°. The amount of frequency change [math]\displaystyle{ \Delta \omega }[/math] caused by a given phase change [math]\displaystyle{ \Delta \phi }[/math] depends on the slope of the loop phase curve at [math]\displaystyle{ \omega_0 }[/math], which is determined by the [math]\displaystyle{ Q }[/math][19][20][21] [22]

[math]\displaystyle{ {d\phi \over d\omega}\Bigg|_{\omega_0} = -{2Q \over \omega_0}\, }[/math]      so      [math]\displaystyle{ \Delta \omega = -{\omega_0 \over 2Q}\Delta \phi \, }[/math]

RC oscillators have the equivalent of a very low [math]\displaystyle{ Q }[/math], so the phase changes very slowly with frequency, therefore a given phase change will cause a large change in the frequency. In contrast, LC oscillators have tank circuits with high [math]\displaystyle{ Q }[/math] (~102). This means the phase shift of the feedback network increases rapidly with frequency near the resonant frequency of the tank circuit.[19] So a large change in phase causes only a small change in frequency. Therefore the circuit's oscillation frequency is very close to the natural resonant frequency of the tuned circuit, and doesn't depend much on other components in the circuit. The quartz crystal resonators used in crystal oscillators have even higher [math]\displaystyle{ Q }[/math] (104 to 106)[22] and their frequency is very stable and independent of other circuit components.

Tunability

The frequency of RC and LC oscillators can be tuned over a wide range by using variable components in the filter. A microwave cavity can be tuned mechanically by moving one of the walls. In contrast, a quartz crystal is a mechanical resonator whose resonant frequency is mainly determined by its dimensions, so a crystal oscillator's frequency is only adjustable over a very narrow range, a tiny fraction of one percent.[5]:p.39–40[23][24][25][26] [27] [28] It's frequency can be changed slightly by using a trimmer capacitor in series or parallel with the crystal.[5]:p.39–40

Startup and amplitude of oscillation

The Barkhausen criterion above, eqs. (1) and (2), merely gives the frequencies at which steady-state oscillation is possible, but says nothing about the amplitude of the oscillation, whether the amplitude is stable, or whether the circuit will start oscillating when the power is turned on.[29][14]:p.5[30] For a practical oscillator two additional requirements are necessary:

  • In order for oscillations to start up in the circuit from zero, the circuit must have "excess gain"; the loop gain for small signals must be greater than one at its oscillation frequency[16][11][17][14]:p.3–5[30]
[math]\displaystyle{ |A\beta(j\omega_0)| \gt 1\, }[/math]
  • For stable operation, the feedback loop must include a nonlinear component which reduces the gain back to unity as the amplitude increases to its operating value.[16][11]

A typical rule of thumb is to make the small signal loop gain at the oscillation frequency 2 or 3.[31][17] When the power is turned on, oscillation is started by the power turn-on transient or random electronic noise present in the circuit.[14]:p.5[5]:p.113–114 Noise guarantees that the circuit will not remain "balanced" precisely at its unstable DC equilibrium point (Q point) indefinitely. Due to the narrow passband of the filter, the response of the circuit to a noise pulse will be sinusoidal, it will excite a small sine wave of voltage in the loop. Since for small signals the loop gain is greater than one, the amplitude of the sine wave increases exponentially.[16][11]

During startup, while the amplitude of the oscillation is small, the circuit is approximately linear, so the analysis used in the Barkhausen criterion is applicable. When the amplitude becomes large enough that the amplifier becomes nonlinear, technically the frequency domain analysis used in normal amplifier circuits is no longer applicable, so the "gain" of the circuit is undefined. However the filter attenuates the harmonic components produced by the nonlinearity of the amplifier, so the fundamental frequency component [math]\displaystyle{ \sin \omega_0 t }[/math] mainly determines the loop gain[32] (this is the "harmonic balance" analysis technique for nonlinear circuits).

The sine wave cannot grow indefinitely; in all real oscillators some nonlinear process in the circuit limits its amplitude,[16][33][5]:p.120 reducing the gain as the amplitude increases, resulting in stable operation at some constant amplitude.[16] In most oscillators this nonlinearity is simply the saturation (limiting) of the amplifying device, the transistor, vacuum tube or op-amp.[31][34][35][14]:p.5 The maximum voltage swing of the amplifier's output is limited by the DC voltage provided by its power supply. Another possibility is that the output may be limited by the amplifier slew rate.

As the amplitude of the output nears the power supply voltage rails, the amplifier begins to saturate on the peaks (top and bottom) of the sine wave, flattening or "clipping" the peaks.[18] Since the output of the amplifier can no longer increase with increasing input, further increases in amplitude cause the equivalent gain of the amplifier and thus the loop gain to decrease.[30] The amplitude of the sine wave, and the resulting clipping, continues to grow until the loop gain is reduced to unity, [math]\displaystyle{ |A\beta(j\omega_0)|\;=\;1\, }[/math], satisfying the Barkhausen criterion, at which point the amplitude levels off and steady state operation is achieved,[16] with the output a slightly distorted sine wave with peak amplitude determined by the supply voltage. This is a stable equilibrium; if the amplitude of the sine wave increases for some reason, increased clipping of the output causes the loop gain [math]\displaystyle{ |A\beta(j\omega_0)| }[/math] to drop below one temporarily, reducing the sine wave's amplitude back to its unity-gain value. Similarly if the amplitude of the wave decreases, the decreased clipping will cause the loop gain to increase above one, increasing the amplitude.

The amount of harmonic distortion in the output is dependent on how much excess loop gain the circuit has:[30][31][18][11]

  • If the small signal loop gain is made close to one, just slightly greater, the output waveform will have minimum distortion, and the frequency will be most stable and independent of supply voltage and load impedance. However, the oscillator may be slow starting up, and a small decrease in gain due to a variation in component values may prevent it from oscillating.
  • If the small signal loop gain is made significantly greater than one, the oscillator starts up faster, but more severe clipping of the sine wave occurs, and thus the resulting distortion of the output waveform increases. The oscillation frequency becomes more dependent on the supply voltage and current drawn by the load.[18]

An exception to the above are high Q oscillator circuits such as crystal oscillators; the narrow bandwidth of the crystal removes the harmonics from the output, producing a 'pure' sinusoidal wave with almost no distortion even with large loop gains.

Design procedure

Since oscillators depend on nonlinearity for their operation, the usual linear frequency domain circuit analysis techniques used for amplifiers based on the Laplace transform, such as root locus and gain and phase plots (Bode plots), cannot capture their full behavior.[29] To determine startup and transient behavior and calculate the detailed shape of the output waveform, electronic circuit simulation computer programs like SPICE are used.[29] A typical design procedure for oscillator circuits is to use linear techniques such as the Barkhausen stability criterion or Nyquist stability criterion to design the circuit, then simulate the circuit on computer to make sure it starts up reliably and to determine the nonlinear aspects of operation such as harmonic distortion.[11][29][31] Component values are tweaked until the simulation results are satisfactory. The distorted oscillations of real-world (nonlinear) oscillators are called limit cycles and are studied in nonlinear control theory.

Amplitude-stabilized oscillators

In applications where a 'pure' very low distortion sine wave is needed, such as precision signal generators, a nonlinear component is often used in the feedback loop that provides a 'slow' gain reduction with amplitude. This stabilizes the loop gain at an amplitude below the saturation level of the amplifier, so it does not saturate and "clip" the sine wave. Resistor-diode networks and FETs are often used for the nonlinear element. An older design uses a thermistor or an ordinary incandescent light bulb; both provide a resistance that increases with temperature as the current through them increases.

As the amplitude of the signal current through them increases during oscillator startup, the increasing resistance of these devices reduces the loop gain. The essential characteristic of all these circuits is that the nonlinear gain-control circuit must have a long time constant, much longer than a single period of the oscillation. Therefore over a single cycle they act as virtually linear elements, and so introduce very little distortion. The operation of these circuits is somewhat analogous to an automatic gain control (AGC) circuit in a radio receiver. The Wein bridge oscillator is a widely used circuit in which this type of gain stabilization is used.

Frequency limitations

At high frequencies it becomes difficult to physically implement feedback oscillators because of shortcomings of the components. Since at high frequencies the tank circuit has very small capacitance and inductance, parasitic capacitance and parasitic inductance of component leads and PCB traces become significant. These may create unwanted feedback paths between the output and input of the active device, creating instability and oscillations at unwanted frequencies (parasitic oscillation). Parasitic feedback paths inside the active device itself, such as the interelectrode capacitance between output and input, make the device unstable. The input impedance of the active device falls with frequency, so it may load the feedback network. As a result, stable feedback oscillators are difficult to build for frequencies above 500 MHz, and negative resistance oscillators are usually used for frequencies above this.

History

The first practical oscillators were based on electric arcs, which were used for lighting in the 19th century. The current through an arc light is unstable due to its negative resistance, and often breaks into spontaneous oscillations, causing the arc to make hissing, humming or howling sounds[36]:p.161–165 which had been noticed by Humphry Davy in 1821, Benjamin Silliman in 1822,[37] Auguste Arthur de la Rive in 1846,[38] and David Edward Hughes in 1878.[39] Ernst Lecher in 1888 showed that the current through an electric arc could be oscillatory.[40][41][42]

An oscillator was built by Elihu Thomson in 1892[43][44] by placing an LC tuned circuit in parallel with an electric arc and included a magnetic blowout. Independently, in the same year, George Francis FitzGerald realized that if the damping resistance in a resonant circuit could be made zero or negative, the circuit would produce oscillations, and, unsuccessfully, tried to build a negative resistance oscillator with a dynamo, what would now be called a parametric oscillator.[45][36]:p.161–165 The arc oscillator was rediscovered and popularized by William Duddell in 1900.[46][47] Duddell, a student at London Technical College, was investigating the hissing arc effect. He attached an LC circuit (tuned circuit) to the electrodes of an arc lamp, and the negative resistance of the arc excited oscillation in the tuned circuit.[36]:p.161–165 Some of the energy was radiated as sound waves by the arc, producing a musical tone. Duddell demonstrated his oscillator before the London Institute of Electrical Engineers by sequentially connecting different tuned circuits across the arc to play the national anthem "God Save the Queen".[36]:p.161–165 Duddell's "singing arc" did not generate frequencies above the audio range. In 1902 Danish physicists Valdemar Poulsen and P. O. Pederson were able to increase the frequency produced into the radio range by operating the arc in a hydrogen atmosphere with a magnetic field, inventing the Poulsen arc radio transmitter, the first continuous wave radio transmitter, which was used through the 1920s.[48][49][50]

A 120 MHz oscillator from 1938 using a parallel rod transmission line resonator (Lecher line). Transmission lines are widely used for UHF oscillators.

The vacuum-tube feedback oscillator was invented around 1912, when it was discovered that feedback ("regeneration") in the recently invented audion (triode) vacuum tube could produce oscillations. At least six researchers independently made this discovery, although not all of them can be said to have a role in the invention of the oscillator.[51][52] In the summer of 1912, Edwin Armstrong observed oscillations in audion radio receiver circuits[53] and went on to use positive feedback in his invention of the regenerative receiver.[54][55] Austrian Alexander Meissner independently discovered positive feedback and invented oscillators in March 1913.[53][56] Irving Langmuir at General Electric observed feedback in 1913.[56] Fritz Lowenstein may have preceded the others with a crude oscillator in late 1911.[57] In Britain, H. J. Round patented amplifying and oscillating circuits in 1913.[53] In August 1912, Lee De Forest, the inventor of the audion, had also observed oscillations in his amplifiers, but he didn't understand the significance and tried to eliminate it[58][59] until he read Armstrong's patents in 1914,[60] which he promptly challenged.[61] Armstrong and De Forest fought a protracted legal battle over the rights to the "regenerative" oscillator circuit[61][62] which has been called "the most complicated patent litigation in the history of radio".[63] De Forest ultimately won before the Supreme Court in 1934 on technical grounds, but most sources regard Armstrong's claim as the stronger one.[59][61]

The first and most widely used relaxation oscillator circuit, the astable multivibrator, was invented in 1917 by French engineers Henri Abraham and Eugene Bloch.[64][65][66] They called their cross-coupled, dual-vacuum-tube circuit a multivibrateur, because the square-wave signal it produced was rich in harmonics,[65][66] compared to the sinusoidal signal of other vacuum-tube oscillators.

Vacuum-tube feedback oscillators became the basis of radio transmission by 1920. However, the triode vacuum tube oscillator performed poorly above 300 MHz because of interelectrode capacitance.[citation needed] To reach higher frequencies, new "transit time" (velocity modulation) vacuum tubes were developed, in which electrons traveled in "bunches" through the tube. The first of these was the Barkhausen–Kurz oscillator (1920), the first tube to produce power in the UHF range. The most important and widely used were the klystron (R. and S. Varian, 1937) and the cavity magnetron (J. Randall and H. Boot, 1940).

Mathematical conditions for feedback oscillations, now called the Barkhausen criterion, were derived by Heinrich Georg Barkhausen in 1921. The first analysis of a nonlinear electronic oscillator model, the Van der Pol oscillator, was done by Balthasar van der Pol in 1927.[67] He showed that the stability of the oscillations (limit cycles) in actual oscillators was due to the nonlinearity of the amplifying device. He originated the term "relaxation oscillation" and was first to distinguish between linear and relaxation oscillators. Further advances in mathematical analysis of oscillation were made by Hendrik Wade Bode and Harry Nyquist[68] in the 1930s. In 1969 Kaneyuki Kurokawa derived necessary and sufficient conditions for oscillation in negative-resistance circuits,[69] which form the basis of modern microwave oscillator design.[10]

See also

References

  1. ↑ 1.0 1.1 Snelgrove, Martin (2011). "Oscillator". McGraw-Hill. http://accessscience.com/abstract.aspx?id=477900&referURL=http%3a%2f%2faccessscience.com%2fcontent.aspx%3fid%3d477900. 
  2. ↑ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 2.11 2.12 Chattopadhyay, D. (2006). Electronics (fundamentals And Applications). New Age International. pp. 224–225. ISBN 978-81-224-1780-7. https://books.google.com/books?id=n0rf9_2ckeYC&q=%22negative+resistance%22&pg=PA224. 
  3. ↑ Horowitz, Paul; Hill, Winfield (2015). The Art of Electronics. USA. pp. 425. ISBN 978-0-521-80926-9. 
  4. ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 Garg, Rakesh Kumar; Ashish Dixit; Pavan Yadav (2008). Basic Electronics. Firewall Media. pp. 280. ISBN 978-8131803028. https://books.google.com/books?id=9SOdnsHA2IYC&pg=PA280. 
  5. ↑ 5.0 5.1 5.2 5.3 5.4 Gottlieb, Irving M. (1997). Practical Oscillator Handbook. Elsevier. ISBN 0080539386. https://books.google.com/books?id=e_oZ69GAuxAC&dq=pull+pulling&pg=PA40. 
  6. ↑ APITech. "SAW Technology" (in en). https://info.apitech.com/saw-technology-va. 
  7. ↑ 7.0 7.1 7.2 Kung, Fabian Wai Lee (2009). "Lesson 9: Oscillator Design". Prof. Kung's website, Multimedia University. http://pesona.mmu.edu.my/~wlkung/ADS/rf/lesson9.pdf. , Sec. 3 Negative Resistance Oscillators, pp. 9–10, 14
  8. ↑ 8.0 8.1 8.2 8.3 Räisänen, Antti V.; Arto Lehto (2003). Radio Engineering for Wireless Communication and Sensor Applications. USA: Artech House. pp. 180–182. ISBN 978-1580535427. https://books.google.com/books?id=m8Dgkvf84xoC&pg=PA181. 
  9. ↑ 9.0 9.1 Ellinger, Frank (2008). Radio Frequency Integrated Circuits and Technologies, 2nd Ed. USA: Springer. pp. 391–394. ISBN 978-3540693246. https://books.google.com/books?id=0pl9xYD0QNMC&pg=PA391. 
  10. ↑ 10.0 10.1 Maas, Stephen A. (2003). Nonlinear Microwave and RF Circuits, 2nd Ed. Artech House. pp. 542–544. ISBN 978-1580534840. https://books.google.com/books?id=SSw6gWLG-d4C&pg=PA542. 
  11. ↑ 11.0 11.1 11.2 11.3 11.4 11.5 11.6 11.7 Schubert, Thomas F. Jr.; Kim, Ernest M. (2016). Fundamentals of Electronics. Book 4: Oscillators and Advanced Electronics Topics. Morgan and Claypool. pp. 926–928. ISBN 978-1627055697. https://books.google.com/books?id=uNQlDAAAQBAJ&dq=nonlinearity&pg=PA927. 
  12. ↑ Sobot, Robert (2012). Wireless Communication Electronics: Introduction to RF Circuits and Design Techniques. Springer Science and Business Media. pp. 221–222. ISBN 978-1461411161. https://books.google.com/books?id=SdGaiV6iup0C&dq=oscillator+gain+phase+barkhausen&pg=PA221. 
  13. ↑ 13.0 13.1 13.2 13.3 13.4 13.5 Carr, Joe (2002). RF Components and Circuits. Newnes. pp. 125–126. ISBN 0080498078. https://books.google.com/books?id=V9gBTNvt3zIC&dq=barkhausen+inverting*180+%22phase+shift%22&pg=PA126. 
  14. ↑ 14.0 14.1 14.2 14.3 14.4 14.5 14.6 14.7 14.8 Gonzalez, Guillermo (2006). Foundations of Oscillator Circuit Design. Artech House. ISBN 9781596931633. http://www.artechhouse.com/uploads/public/documents/chapters/Gonzalez-162_CH01.pdf. 
  15. ↑ Maas, Stephen A. (2003). Nonlinear Microwave and RF Circuits. Artech House. pp. 537–540. ISBN 1580536115. https://books.google.com/books?id=SSw6gWLG-d4C&dq=gain+phase&pg=PA537. 
  16. ↑ 16.0 16.1 16.2 16.3 16.4 16.5 16.6 16.7 16.8 16.9 Lesurf, Jim (2006). "Feedback Oscillators". The Scots Guide to Electronics. School of Physics and Astronomy, Univ. of St. Andrewes, Scotland. https://www.st-andrews.ac.uk/~www_pa/Scots_Guide/RadCom/part4/page1.html. 
  17. ↑ 17.0 17.1 17.2 17.3 Razavi, Behzad (2001). Design of Analog CMOS Integrated Circuits. The McGraw-Hill Companies. pp. 482–484. ISBN 7302108862. https://books.google.com/books?id=hl6JZ8DKlFwC&dq=Barkhausen&pg=PA483. 
  18. ↑ 18.0 18.1 18.2 18.3 Carter, Bruce; Mancini, Ron (2009). Op Amps for Everyone, 3rd Ed.. Elsevier. pp. 345–347. ISBN 9781856175050. https://books.google.com/books?id=nnCNsjpicJIC&pg=PA346. 
  19. ↑ 19.0 19.1 19.2 19.3 Stephan, Karl (2015). Analog and Mixed-Signal Electronics. John Wiley and Sons. pp. 192–193. ISBN 978-1119051800. https://books.google.com/books?id=cDAABwAAQBAJ&pg=PA192. 
  20. ↑ 20.0 20.1 Vidkjaer, Jens. "Ch. 6: Oscillators". Class Notes: 31415 RF Communications Circuits. Technical Univ. of Denmark. http://rftoolbox.dtu.dk/book/Ch6.pdf.  p. 8-9
  21. ↑ Huijsing, Johan; van de Plassche, Rudy J.; Sansen, Willy (2013). Analog Circuit Design. Springer Scientific and Business Media. pp. 77. ISBN 978-1475724622. https://books.google.com/books?id=B8fSBwAAQBAJ&pg=PA77. 
  22. ↑ 22.0 22.1 Kazimierczuk, Marian K. (2014). RF Power Amplifiers, 2nd Ed.. John Wiley and Sons. pp. 586–587. ISBN 978-1118844335. https://books.google.com/books?id=-U7YBAAAQBAJ&pg=PA587. 
  23. ↑ Froehlich, Fritz E.; Kent, Allen (1991). The Froehlich/Kent Encyclopedia of Telecommunications, Volume 3. CRC Press. pp. 448. ISBN 0824729021. https://books.google.com/books?id=QQcfD_iWlPYC&dq=%22crystal+oscillator%22+tuning+stiffness&pg=PA448. 
  24. ↑ Misra, Devendra (2004). Radio-Frequency and Microwave Communication Circuits: Analysis and Design. John Wiley. pp. 494. ISBN 0471478733. https://books.google.com/books?id=7nWN_pGQKnMC&dq=%22crystal+oscillator%22+pulling+%22tuning+range%22&pg=PA494. 
  25. ↑ Terman, Frederick E. (1943). Radio Engineer's Handbook. McGraw-Hill. pp. 497. http://www.itermoionici.it/letteratura_files/Radio-Engineers-Handbook.pdf. 
  26. ↑ "Oscillator Application Notes". Support. Frequency Management International, CA. http://www.frequencymanagement.com/web_pdfs/cat_pdfs_applicationNotes/45-49.PDF. 
  27. ↑ Scroggie, M. G.; Amos, S. W. (2013). Foundations of Wireless and Electronics. Elsevier. pp. 241–242. ISBN 978-1483105574. https://books.google.com/books?id=ihABBQAAQBAJ&dq=%22fixed+frequency%22+%22hardly+anything+about+it+that+can+vary%22&pg=PA242. 
  28. ↑ Vig, John R. and Ballato, Arthur "Frequency Control Devices" in Thurston, R. N.; Pierce, Allan D.; Papadakis, Emmanuel P. (1998). Reference for Modern Instrumentation, Techniques, and Technology: Ultrasonic Instruments and Devices II. Elsevier. pp. 227. ISBN 0080538916. https://books.google.com/books?id=0lvCkB6y4dwC&dq=%22crystal+oscillator%22+tuning+stiffness&pg=PA227. 
  29. ↑ 29.0 29.1 29.2 29.3 Stephan, Karl (2015). Analog and Mixed-Signal Electronics. John Wiley and Sons. pp. 187–188. ISBN 978-1119051800. https://books.google.com/books?id=cDAABwAAQBAJ&pg=PA188. 
  30. ↑ 30.0 30.1 30.2 30.3 "Sinusoidal Oscillators" (DOC). Course notes: ECE3434 Advanced Electronic Circuits. Electrical and Computer Engineering Dept., Mississippi State University. Summer 2015. http://courses.ece.msstate.edu/ece3434/notes/oscillators/Oscillator.doc. , p. 4-7
  31. ↑ 31.0 31.1 31.2 31.3 Rhea, Randall W. (2014). Discrete Oscillator Design: Linear, Nonlinear, Transient, and Noise Domains. Artech House. pp. 11–12. ISBN 978-1608070480. https://books.google.com/books?id=4Op56QdHFPUC&pg=PA11. 
  32. ↑ Toumazou, Chris; Moschytz, George S.; Gilbert, Barrie (2004). Trade-Offs in Analog Circuit Design: The Designer's Companion, Part 1. Springer Science and Business Media. pp. 565–566. ISBN 9781402080463. https://books.google.com/books?id=VoBIOvirkiMC&dq=nonlinear&pg=PA565. 
  33. ↑ Roberge, James K. (1975). Operational Amplifiers: Theory and Practice. John Wiley and Sons. pp. 487–488. ISBN 0471725854. http://ocw.mit.edu/resources/res-6-010-electronic-feedback-systems-spring-2013/textbook/MITRES_6-010S13_chap12.pdf. 
  34. ↑ van der Tang, J.; Kasperkovitz, Dieter; van Roermund, Arthur (2006). High-Frequency Oscillator Design for Integrated Transceivers. Springer Science and Business Media. pp. 51. ISBN 0306487160. https://books.google.com/books?id=0rniokw7bLkC&dq=%22amplitude+stabilization%22+self-limiting&pg=PT51. 
  35. ↑ Razavi, Behzad (2001) Design of Analog CMOS Integrated Circuits, p. 487-489
  36. ↑ 36.0 36.1 36.2 36.3 Hong, Sungook (2001). Wireless: From Marconi's Black-Box to the Audion. MIT Press. ISBN 978-0262082983. https://books.google.com/books?id=UjXGQSPXvIcC&pg=PA165. 
  37. ↑ Silliman, Benjamin (1859). First Principles of Physics: Or Natural Philosophy, Designed for the Use of Schools and Colleges. H.C. Peck & T. Bliss. p. 629. https://archive.org/details/firstprinciples05sillgoog. "Davy Silliman Hissing." 
  38. ↑ "Wireless telephony, in theory and practice". N.Y. Van Nostrand. 1908. https://archive.org/details/wirelesstelephon00ruhmrich. 
  39. ↑ Casperson, L. W (1991). "The humming telephone as an acoustic maser". Optical and Quantum Electronics 23 (8): 995–1010. doi:10.1007/BF00611436. 
  40. ↑ Anders, André (2009). Cathodic Arcs: From Fractal Spots to Energetic Condensation. Springer Science and Business Media. pp. 31–32. ISBN 978-0387791081. https://books.google.com/books?id=rwIUhsbBHQYC&pg=PA31. 
  41. ↑ Cady, W. G.; Arnold, H. D. (1907). "On the electric arc between metallic electrodes". American Journal of Science 24 (143): 406. https://books.google.com/books?id=0KD0BuvSOokC&pg=PA406. Retrieved April 12, 2017. 
  42. ↑ "Notes". The Electrical Review 62 (1578): 812. February 21, 1908. https://books.google.com/books?id=it9QAAAAYAAJ&pg=PA312. Retrieved April 12, 2017. 
  43. ↑ Morse 1925, p. 23
  44. ↑ Thomson, Elihu, "Method of and Means for Producing Alternating Currents", US patent 500630, published 18 July 1892, issued 4 July 1893
  45. ↑ G. Fitzgerald, On the Driving of Electromagnetic Vibrations by Electromagnetic and Electrostatic Engines, read at the January 22, 1892, meeting of the Physical Society of London, in Larmor, Joseph, ed (1902). The Scientific Writings of the late George Francis Fitzgerald. London: Longmans, Green and Co.. pp. 277–281. https://books.google.com/books?id=G0bPAAAAMAAJ&pg=PA277. 
  46. ↑ Morse 1925, pp. 80–81
  47. ↑ Duddell, William du Bois, "Improvements in and connected with Means for the Conversion of Electrical Energy, Derived from a Source of Direct Current, into Varying or Alternating Currents", GB patent 190021629, published 29 Nov 1900, issued 23 Nov 1901
  48. ↑ Morse 1925, p. 31
  49. ↑ Poulsen, Valdemar, "Improvements relating to the Production of Alternating Electric Currents", GB patent 190315599, issued 14 July 1904
  50. ↑ Poulsen, Valdemar, "Method of Producing Alternating Currents with a High Number of Vibrations", US patent 789449, issued 9 May 1905
  51. ↑ Hempstead, Colin; William E. Worthington (2005). Encyclopedia of 20th-Century Technology. 2. Taylor & Francis. p. 648. ISBN 978-1579584641. https://books.google.com/books?id=0wkIlnNjDWcC&pg=PA648. 
  52. ↑ Hong 2001, p. 156
  53. ↑ 53.0 53.1 53.2 Fleming, John Ambrose (1919). The Thermionic Valve and its Developments in Radiotelegraphy and Telephony. London: The Wireless Press. pp. 148–155. https://books.google.com/books?id=ZBtDAAAAIAAJ&pg=PA148. 
  54. ↑ Hong, Sungook (2003). "A history of the regeneration circuit: From invention to patent litigation". IEEE. http://www.ieeeghn.org/wiki/images/0/08/Hong.pdf. Retrieved August 29, 2012. , pp. 9–10
  55. ↑ Armstrong, Edwin H. (September 1915). "Some recent developments in the Audion receiver". Proc. IRE 3 (9): 215–247. doi:10.1109/jrproc.1915.216677. http://www.ieee.org/documents/00573757.pdf. Retrieved August 29, 2012. 
  56. ↑ 56.0 56.1 Hong 2003, p. 13
  57. ↑ Hong 2003, p. 5
  58. ↑ Hong 2003, pp. 6–7
  59. ↑ 59.0 59.1 Hijiya, James A. (1992). Lee De Forest and the Fatherhood of Radio. Lehigh University Press. pp. 89–90. ISBN 978-0934223232. https://books.google.com/books?id=JYylHhmoNZ4C&pg=PA89. 
  60. ↑ Hong 2003, p. 14
  61. ↑ 61.0 61.1 61.2 Nahin, Paul J. (2001). The Science of Radio: With Matlab and Electronics Workbench Demonstration, 2nd Ed. Springer. pp. 280. ISBN 978-0387951508. https://books.google.com/books?id=V1GBW6UD4CcC&pg=PA82. 
  62. ↑ Hong 2001, pp. 181–189
  63. ↑ Hong 2003, p. 2
  64. ↑ Abraham, H.; E. Bloch (1919). "Measurement of period of high frequency oscillations". Comptes Rendus 168: 1105. 
  65. ↑ 65.0 65.1 Glazebrook, Richard (1922). A Dictionary of Applied Physics, Vol. 2: Electricity. London: Macmillan and Co. Ltd.. pp. 633–634. https://books.google.com/books?id=bavQAAAAMAAJ&pg=PA633. 
  66. ↑ 66.0 66.1 Calvert, James B. (2002). "The Eccles-Jordan Circuit and Multivibrators". Dr. J. B. Calvert website, Univ. of Denver. http://mysite.du.edu/~etuttle/electron/elect36.htm. 
  67. ↑ Van der Pol, Balthazar (1927). "On relaxation-oscillations". The London, Edinburgh and Dublin Philosophical Magazine 2 (7): 978–992. doi:10.1080/14786442608564127. 
  68. ↑ Nyquist, H. (January 1932). "Regeneration Theory". Bell System Tech. J. 11 (1): 126–147. doi:10.1002/j.1538-7305.1932.tb02344.x. http://www3.alcatel-lucent.com/bstj/vol11-1932/articles/bstj11-1-126.pdf. Retrieved December 5, 2012.  on Alcatel-Lucent website
  69. ↑ Kurokawa, Kaneyuki (July 1969). "Some Basic Characteristics of Broadband Negative Resistance Oscillator Circuits". Bell System Tech. J. 48 (6): 1937–1955. doi:10.1002/j.1538-7305.1969.tb01158.x. http://www3.alcatel-lucent.com/bstj/vol48-1969/articles/bstj48-6-1937.pdf. Retrieved December 8, 2012.  Eq. 10 is a necessary condition for oscillation; eq. 12 is a sufficient condition,
  • Morse, A. H. (1925), Radio: Beam and Broadcast: Its story and patents, London: Ernest Benn, https://archive.org/details/radiobeamandbroa029214mbp . History of radio in 1925. Oscillator claims 1912; De Forest and Armstrong court case cf p. 45. Telephone hummer/oscillator by A. S. Hibbard in 1890 (carbon microphone has power gain); Larsen "used the same principle in the production of alternating current from a direct current source"; accidental development of vacuum tube oscillator; all at p. 86. Von Arco and Meissner first to recognize application to transmitter; Round for first transmitter; nobody patented triode transmitter at p. 87.

Further reading

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Engineering:Electronic_oscillator&oldid=3413391"