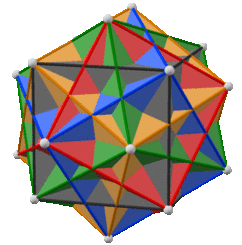
Compound of four cubes
| Compound of four cubes | |
|---|---|
 (Animation) | |
| Type | Compound |
| Convex hull | Chamfered cube |
| Polyhedra | 4 cubes |
| Faces | 32 squares |
| Edges | 48 |
| Vertices | 32 (8 + 24) |
| Symmetry group | octahedral (Oh) |
| Subgroup restricting to one constituent | 3-fold antiprismatic (D3d) |
The compound of four cubes or Bakos compound[1] is a face-transitive polyhedron compound of four cubes with octahedral symmetry. It is the dual of the compound of four octahedra. Its surface area is 687/77 square lengths of the edge.[2]
Its Cartesian coordinates are (±3, ±3, ±3) and the permutations of (±5, ±1, ±1).
|
Views from 2-fold, 3-fold and 4-fold symmetry axis |
Extension with fifth cube
The eight vertices on the 3-fold symmetry axes can be seen as the vertices of a fifth cube of the same size.[3] Referring to the images below, the four old cubes are called colored, and the new one black. Each colored cube has two opposite vertices on a 3-fold symmetry axis, which are shared with the black cube. (In the picture both 3-fold vertices of the green cube are visible.) The remaining six vertices of each colored cube correspond to the faces of the black cube. This compound shares these properties with the compound of five cubes (related to the dodecahedron), into which it can be transformed by rotating the colored cubes on their 3-fold axes.
|
Extension (see animation) and its transition to the icosahedral compound |
See also
- Compound of three octahedra
- Compound of five octahedra
- Compound of ten octahedra
- Compound of twenty octahedra
- Compound of three cubes
- Compound of five cubes
- Compound of six cubes
- Uniform polyhedron compound
References
- ↑ WOLFRAM Demonstrations Project: The Bakos Compound
- ↑ Weisstein, Eric W.. "Cube 4-Compound". Wolfram. http://mathworld.wolfram.com/Cube4-Compound.html.
- ↑ The Wolfram page Cube 5-Compound shows a small picture of this extension under the name "first cube 4-compound". Also Grant Sanderson has used a picture of it to illustrate the term symmetry.
 |