Computational complexity of matrix multiplication

Short description: Algorithmic runtime requirements for matrix multiplication

Unsolved problem in computer science: What is the fastest algorithm for matrix multiplication? (more unsolved problems in computer science)

In theoretical computer science, the computational complexity of matrix multiplication dictates how quickly the operation of matrix multiplication can be performed. Matrix multiplication algorithms are a central subroutine in theoretical and numerical algorithms for numerical linear algebra and optimization, so finding the fastest algorithm for matrix multiplication is of major practical relevance.

Directly applying the mathematical definition of matrix multiplication gives an algorithm that requires n³ field operations to multiply two n × n matrices over that field (Θ(n³) in big O notation). Surprisingly, algorithms exist that provide better running times than this straightforward "schoolbook algorithm". The first to be discovered was Strassen's algorithm, devised by Volker Strassen in 1969 and often referred to as "fast matrix multiplication". The optimal number of field operations needed to multiply two square n × n matrices up to constant factors is still unknown. This is a major open question in theoretical computer science.

(As of July 2023), the best announced bound on the asymptotic complexity of a matrix multiplication algorithm is O(n^2.371552) time, given by Williams, Xu, Xu, and Zhou, announced in a preprint. This improves on the bound of O(n^2.371866) given by a preprint of Duan, Wu and Zhou. However, this and similar improvements to Strassen are not used in practice, because they are galactic algorithms: the constant coefficient hidden by the Big O notation is so large that they are only worthwhile for matrices that are too large to handle on present-day computers. The best time-bound confirmed by peer review is O(n^2.3728596).

Simple algorithms

If A, B are n × n matrices over a field, then their product AB is also an n × n matrix over that field, defined entrywise as

[math]\displaystyle{ (AB)_{ij} = \sum_{k = 1}^n A_{ik} B_{kj}. }[/math]

Schoolbook algorithm

The simplest approach to computing the product of two n × n matrices A and B is to compute the arithmetic expressions coming from the definition of matrix multiplication. In pseudocode:

input A and B, both n by n matrices
initialize C to be an n by n matrix of all zeros
for i from 1 to n:
    for j from 1 to n:
        for k from 1 to n:
            C[i][j] = C[i][j] + A[i][k]*B[k][j]
output C (as A*B)

This algorithm requires, in the worst case, [math]\displaystyle{ n^3 }[/math] multiplications of scalars and [math]\displaystyle{ n^3 - n^2 }[/math] additions for computing the product of two square n×n matrices. Its computational complexity is therefore [math]\displaystyle{ O(n^3) }[/math], in a model of computation where field operations (addition and multiplication) take constant time (in practice, this is the case for floating point numbers, but not necessarily for integers).

Strassen's algorithm

Strassen's algorithm improves on naive matrix multiplication through a divide-and-conquer approach. The key observation is that multiplying two 2 × 2 matrices can be done with only 7 multiplications, instead of the usual 8 (at the expense of 11 additional addition and subtraction operations). This means that, treating the input n×n matrices as block 2 × 2 matrices, the task of multiplying n×n matrices can be reduced to 7 subproblems of multiplying n/2×n/2 matrices. Applying this recursively gives an algorithm needing [math]\displaystyle{ O( n^{\log_{2}7}) \approx O(n^{2.807}) }[/math] field operations.

Unlike algorithms with faster asymptotic complexity, Strassen's algorithm is used in practice. The numerical stability is reduced compared to the naive algorithm, but it is faster in cases where n > 100 or so and appears in several libraries, such as BLAS. Fast matrix multiplication algorithms cannot achieve component-wise stability, but some can be shown to exhibit norm-wise stability. It is very useful for large matrices over exact domains such as finite fields, where numerical stability is not an issue.

Matrix multiplication exponent

Improvement of estimates of exponent ω over time for the computational complexity of matrix multiplication [math]\displaystyle{ O(n^\omega) }[/math]

Closeup of 1990–2023

Timeline of matrix multiplication exponent

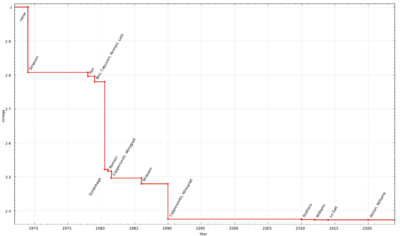
Year	Bound on omega	Authors
1969	2.8074	Strassen
1978	2.796	Pan
1979	2.780	Bini, Milvio Capovani (it), Romani
1981	2.522	Schönhage
1981	2.517	Romani
1981	2.496	Coppersmith, Winograd
1986	2.479	Strassen
1990	2.3755	Coppersmith, Winograd
2010	2.3737	Stothers
2012	2.3729	Williams
2014	2.3728639	Le Gall
2020	2.3728596	Alman, Williams
2022	2.371866	Duan, Wu, Zhou
2023	2.371552	Williams, Xu, Xu, and Zhou

The matrix multiplication exponent, usually denoted ω, is the smallest real number for which any two [math]\displaystyle{ n\times n }[/math] matrices over a field can be multiplied together using [math]\displaystyle{ n^{\omega + o(1)} }[/math] field operations. This notation is commonly used in algorithms research, so that algorithms using matrix multiplication as a subroutine have bounds on running time that can update as bounds on ω improve.

Using a naive lower bound and schoolbook matrix multiplication for the upper bound, one can straightforwardly conclude that 2 ≤ ω ≤ 3. Whether ω = 2 is a major open question in theoretical computer science, and there is a line of research developing matrix multiplication algorithms to get improved bounds on ω.

All recent algorithms in this line of research use the laser method, a generalization of the Coppersmith–Winograd algorithm, which was given by Don Coppersmith and Shmuel Winograd in 1990 and was the best matrix multiplication algorithm until 2010. The conceptual idea of these algorithms is similar to Strassen's algorithm: a way is devised for multiplying two k × k-matrices with fewer than k³ multiplications, and this technique is applied recursively. The laser method has limitations to its power, and cannot be used to show that ω < 2.3725. Duan, Wu and Zhou identify a source of potential optimization in the laser method termed combination loss. They find a way to exploit this to devise a variant of the laser method which they use to show ω < 2.37188, breaking the barrier for any conventional laser method algorithm. With this newer approach another bound applies according to Duan, Wu and Zhou and showing ω < 2.3078 will not be possible only addressing combination loss in the laser method.

Group theory reformulation of matrix multiplication algorithms

Henry Cohn, Robert Kleinberg, Balázs Szegedy and Chris Umans put methods such as the Strassen and Coppersmith–Winograd algorithms in an entirely different group-theoretic context, by utilising triples of subsets of finite groups which satisfy a disjointness property called the triple product property (TPP). They also give conjectures that, if true, would imply that there are matrix multiplication algorithms with essentially quadratic complexity. This implies that the optimal exponent of matrix multiplication is 2, which most researchers believe is indeed the case. One such conjecture is that families of wreath products of Abelian groups with symmetric groups realise families of subset triples with a simultaneous version of the TPP. Several of their conjectures have since been disproven by Blasiak, Cohn, Church, Grochow, Naslund, Sawin, and Umans using the Slice Rank method. Further, Alon, Shpilka and Chris Umans have recently shown that some of these conjectures implying fast matrix multiplication are incompatible with another plausible conjecture, the sunflower conjecture, which in turn is related to the cap set problem.

Lower bounds for ω

There is a trivial lower bound of [math]\displaystyle{ \omega \ge 2 }[/math]. Since any algorithm for multiplying two n × n-matrices has to process all 2n² entries, there is a trivial asymptotic lower bound of Ω(n²) operations for any matrix multiplication algorithm. Thus [math]\displaystyle{ 2\le \omega \lt 2.37188 }[/math]. It is unknown whether [math]\displaystyle{ \omega \gt 2 }[/math]. The best known lower bound for matrix-multiplication complexity is Ω(n² log(n)), for bounded coefficient arithmetic circuits over the real or complex numbers, and is due to Ran Raz.

The exponent ω is defined to be a limit point, in that it is the infimum of the exponent over all matrix multiplication algorithms. It is known that this limit point is not achieved. In other words, under the model of computation typically studied, there is no matrix multiplication algorithm that uses precisely O(n^ω) operations; there must be an additional factor of n^o(1).

Rectangular matrix multiplication

Similar techniques also apply to rectangular matrix multiplication. The central object of study is [math]\displaystyle{ \omega(k) }[/math], which is the smallest [math]\displaystyle{ c }[/math] such that one can multiply a matrix of size [math]\displaystyle{ n\times \lceil n^k\rceil }[/math] with a matrix of size [math]\displaystyle{ \lceil n^k\rceil \times n }[/math] with [math]\displaystyle{ O(n^{c + o(1)}) }[/math] arithmetic operations. A result in algebraic complexity states that multiplying matrices of size [math]\displaystyle{ n\times \lceil n^k\rceil }[/math] and [math]\displaystyle{ \lceil n^k\rceil \times n }[/math] requires the same number of arithmetic operations as multiplying matrices of size [math]\displaystyle{ n\times \lceil n^k\rceil }[/math] and [math]\displaystyle{ n \times n }[/math] and of size [math]\displaystyle{ n \times n }[/math] and [math]\displaystyle{ n\times \lceil n^k\rceil }[/math], so this encompasses the complexity of rectangular matrix multiplication. This generalizes the square matrix multiplication exponent, since [math]\displaystyle{ \omega(1) = \omega }[/math].

Since the output of the matrix multiplication problem is size [math]\displaystyle{ n^2 }[/math], we have [math]\displaystyle{ \omega(k) \geq 2 }[/math] for all values of [math]\displaystyle{ k }[/math]. If one can prove for some values of [math]\displaystyle{ k }[/math] between 0 and 1 that [math]\displaystyle{ \omega(k) \leq 2 }[/math], then such a result shows that [math]\displaystyle{ \omega(k) = 2 }[/math] for those [math]\displaystyle{ k }[/math]. The largest k such that [math]\displaystyle{ \omega(k) = 2 }[/math] is known as the dual matrix multiplication exponent, usually denoted α. α is referred to as the "dual" because showing that [math]\displaystyle{ \alpha = 1 }[/math] is equivalent to showing that [math]\displaystyle{ \omega = 2 }[/math]. Like the matrix multiplication exponent, the dual matrix multiplication exponent sometimes appears in the complexity of algorithms in numerical linear algebra and optimization.

The first bound on α is by Coppersmith in 1982, who showed that [math]\displaystyle{ \alpha \gt 0.17227 }[/math]. The current best peer-reviewed bound on α is [math]\displaystyle{ \alpha \gt 0.31389 }[/math], given by Le Gall and Urrutia. This paper also contains bounds on [math]\displaystyle{ \omega(k) }[/math]. In July 2023 Williams, Xu, Xu, and Zhou claim to show [math]\displaystyle{ \alpha \geq 0.321334 }[/math] in a preprint.

Related problems

Problems that have the same asymptotic complexity as matrix multiplication include determinant, matrix inversion, Gaussian elimination (see next section). Problems with complexity that is expressible in terms of [math]\displaystyle{ \omega }[/math] include characteristic polynomial, eigenvalues (but not eigenvectors), Hermite normal form, and Smith normal form.

Matrix inversion, determinant and Gaussian elimination

In his 1969 paper, where he proved the complexity [math]\displaystyle{ O(n^{\log_2 7}) \approx O(n^{2.807}) }[/math] for matrix computation, Strassen proved also that matrix inversion, determinant and Gaussian elimination have, up to a multiplicative constant, the same computational complexity as matrix multiplication. The proof does not make any assumptions on matrix multiplication that is used, except that its complexity is [math]\displaystyle{ O(n^\omega) }[/math] for some [math]\displaystyle{ \omega \ge 2 }[/math]

The starting point of Strassen's proof is using block matrix multiplication. Specifically, a matrix of even dimension 2n×2n may be partitioned in four n×n blocks

[math]\displaystyle{ \begin{bmatrix} {A} & {B} \\{C} & {D} \end{bmatrix}. }[/math]

Under this form, its inverse is

[math]\displaystyle{ \begin{bmatrix} {A} & {B} \\ {C} & {D} \end{bmatrix}^{-1} = \begin{bmatrix} {A}^{-1}+{A}^{-1}{B}({D}-{CA}^{-1}{B})^{-1}{CA}^{-1} & -{A}^{-1}{B}({D}-{CA}^{-1}{B})^{-1} \\ -({D}-{CA}^{-1}{B})^{-1}{CA}^{-1} & ({D}-{CA}^{-1}{B})^{-1} \end{bmatrix}, }[/math]

provided that A and [math]\displaystyle{ {D}-{CA}^{-1}{B} }[/math] are invertible.

Thus, the inverse of a 2n×2n matrix may be computed with two inversions, six multiplications and four additions or additive inverses of n×n matrices. It follows that, denoting respectively by I(n), M(n) and A(n) = n² the number of operations needed for inverting, multiplying and adding n×n matrices, one has

[math]\displaystyle{ I(2n) \le 2I(n) + 6M(n)+ 4 A(n). }[/math]

If [math]\displaystyle{ n=2^k, }[/math] one may apply this formula recursively:

[math]\displaystyle{ \begin{align} I(2^k) &\le 2I(2^{k-1}) + 6M(2^{k-1})+ 4 A(2^{k-1})\\ &\le 2^2I(2^{k-2}) + 6(M(2^{k-1})+2M(2^{k-2})) + 4(A(2^{k-1}) + 2A(2^{k-2}))\\ &\,\,\,\vdots \end{align} }[/math]

If [math]\displaystyle{ M(n)\le cn^\omega, }[/math] and [math]\displaystyle{ \alpha=2^\omega\ge 4, }[/math] one gets eventually

[math]\displaystyle{ \begin{align} I(2^k) &\le 2^k I(1) + 6c(\alpha^{k-1}+2\alpha^{k-2} + \cdots +2^{k-1}\alpha^0) + k 2^{k+1}\\ &\le 2^k + 6c\frac{\alpha^k-2^k}{\alpha-2} + k 2^{k+1}\\ &\le d(2^k)^\omega \end{align} }[/math]

for some constant d.

For matrices whose dimension is not a power of two, the same complexity is reached by increasing the dimension of the matrix to a power of two, by padding the matrix with rows and columns whose entries are 1 on the diagonal and 0 elsewhere.

This proves the asserted complexity for matrices such that all submatrices that have to be inverted are indeed invertible. This complexity is thus proved for almost all matrices, as a matrix with randomly chosen entries is invertible with probability one.

The same argument applies to LU decomposition, as, if the matrix A is invertible, the equality

[math]\displaystyle{ \begin{bmatrix} {A} & {B} \\{C} & {D} \end{bmatrix} = \begin{bmatrix}I & 0\\CA^{-1}&I\end{bmatrix}\,\begin{bmatrix}A&B\\0&D-CA^{-1}B\end{bmatrix} }[/math]

defines a block LU decomposition that may be applied recursively to [math]\displaystyle{ A }[/math] and [math]\displaystyle{ D-CA^{-1}B, }[/math] for getting eventually a true LU decomposition of the original matrix.

The argument applies also for the determinant, since it results from the block LU decomposition that

[math]\displaystyle{ \det \begin{bmatrix} {A} & {B} \\{C} & {D} \end{bmatrix} = \det(A)\det(D-CA^{-1}B). }[/math]

Minimizing number of multiplications

Related to the problem of minimizing the number of arithmetic operations is minimizing the number of multiplications, which is typically a more costly operation than addition. A [math]\displaystyle{ O(n^\omega) }[/math] algorithm for matrix multiplication must necessarily only use [math]\displaystyle{ O(n^\omega) }[/math] multiplication operations, but these algorithms are impractical. Improving from the naive [math]\displaystyle{ n^3 }[/math] multiplications for schoolbook multiplication, [math]\displaystyle{ 4\times 4 }[/math] matrices in [math]\displaystyle{ \mathbb{Z}/2\mathbb{Z} }[/math] can be done with 47 multiplications, [math]\displaystyle{ 3\times 3 }[/math] matrix multiplication over a commutative ring can be done in 21 multiplications (23 if non-commutative). The lower bound of multiplications needed is 2mn+2n−m−2 (multiplication of n×m-matrices with m×n-matrices using the substitution method, m⩾n⩾3), which means n=3 case requires at least 19 multiplications and n=4 at least 34. For n=2 optimal 7 multiplications 15 additions are minimal, compared to only 4 additions for 8 multiplications.

See also

• Computational complexity of mathematical operations
• CYK algorithm, §Valiant's algorithm
• Freivalds' algorithm, a simple Monte Carlo algorithm that, given matrices A, B and C, verifies in Θ(n²) time if AB = C.
• Matrix chain multiplication
• Matrix multiplication, for abstract definitions
• Matrix multiplication algorithm, for practical implementation details
• Sparse matrix–vector multiplication

External links

• Yet another catalogue of fast matrix multiplication algorithms
• Fawzi, A.; Balog, M.; Huang, A.; Hubert, T.; Romera-Paredes, B.; Barekatain, M.; Novikov, A.; Ruiz, F.J.R. et al. (2022). "Discovering faster matrix multiplication algorithms with reinforcement learning". Nature 610 (7930): 47–53. doi:10.1038/s41586-022-05172-4. PMID 36198780. Bibcode: 2022Natur.610...47F.